基于FPSO的电力巡检机器人的广义二型模糊逻辑控制

作者：吴庆赵涛佃松宜郭锐李胜川方红帏韩吉霞来源：《自动化学报》日期：2022-07-16人气：1293

高压输电线会在环境和机械的作用下出现一些故障或安全隐患, 例如绝缘子老化破损、导线断股、金具氧化腐蚀等, 若不能及时地排除这些问题, 可能会导致重大的事故. 所以高压输电线的巡检一直是供电企业的重要工作. 长时间以来, 我国高压输电线路的巡检工作都是通过人工完成的, 这不仅耗时耗力, 而且高压输电线常常会跨过高山以及江河这些人工难以到达的地方, 从而出现了巡检盲区. 为了使巡检工作变得更加高效和准确, 我国自上世纪90 年代中期开始针对电力巡检机器人(Power-line inspection robot, PLIR)做了大量的研究[1-6], 用PLIR来代替人工进行高压输电线的巡查和维护. PLIR具有较高的效率和可靠性, 并且能轻易到达人工无法到达的巡检盲区. 因此, PLIR的研究具有重大的意义. PLIR在高压输电线上移动时, 需要面对许多的不确定性, 例如风力的干扰和电线的振动, 所以要对它进行控制使其达到平衡. 文献[7-11]提供的方法能够对PLIR的平衡进行控制, 然而这些控制器的设计方法需要利用被控对象精确的物理模型, 并且很少考虑一些不确定因素.

1975年, Mamdani等成功地将I型模糊逻辑控制器(Type-1 fuzzy logic controller, T1FLC)应用在蒸汽机的控制当中[12]. 模糊逻辑控制器的设计不需要依赖精确的数学模型, 而仅需要由专家经验总结出的模糊规则. 不仅如此, 模糊逻辑控制器还具有处理不确定性的能力. 因此, T1FLC得到了大量的研究, 广泛运用于各种领域[13-23]. 广义II型模糊逻辑控制器(General type-2 fuzzy logic controller, GT2FLC)是在T1FLC 的基础上提出来的, GT2FLC具有三维结构的隶属函数, 使得控制系统处理不确定性的能力增强, 所以得到广泛的关注[24-27]. 但同时, 三维结构的隶属函数使得GT2FLC的运算复杂度也增加了许多. 区间II型模糊控制器(Interval type-2 fuzzy logic controller, IT2FLC)相比于GT2FLC, 通过牺牲一些控制性能来减少运算复杂度, 也得到了广泛应用[28-29]. 为了简化广义II型模糊集(General type-2 fuzzy set, GT2FS)的运算, Mendel等[30]提出了用 $α$ 平面来表示广义二型模糊集的方法, GT2FS被分割成若干个区间二型模糊集(Interval type-2 fuzzy set, IT2FS).

在模糊逻辑控制器中, 隶属函数参数的选取对整个控制系统具有极大的影响. 一般情况下, 隶属函数参数的选取多是依赖于经验或者实验数据, 但随着控制精度要求的变高和被控系统的复杂性增加, 传统的参数选取方法已经很难达到要求. 尤其是在GT2FLC中, 三维结构的隶属函数使得整个控制系统无论是参数维数还是复杂度都大大增加. 因此, 在大量文献中, 提出了用优化算法来优化隶属函数参数的方法, 使得控制系统的性能更好[31-35].

粒子群优化算法(Particle swarm optimization, PSO)是应用比较广泛的一种群智能优化算法, 是Eberhart等在对鸟群捕食行为进行研究的基础上提出来的. 此后, 专家提出了许多改进的PSO算法, 并且将其应用于不同的领域上[36-38]. Shi 等[39]在基本的PSO算法上引入了惯性权重这一概念, 提出了标准PSO 算法. 惯性权重在标准PSO算法中具有平衡全局和局部寻优的能力. 在此基础上, 文献[40]提出了一种惯性权重线性递减的方法来改善标准PSO算法的寻优能力. 然而, 对于一些非线性系统, 这种线性递减的惯性权重并不完全适用. 文献[41]提出了一种通过模糊逻辑系统来调整惯性权重的PSO算法, 使得惯性权重的调整更加合理.

本文的创新点如下: 1)针对PLIR平衡调节问题, 设计了GT2FLC; 2) 针对GT2FLC系统中隶属函数参数多并且难以确定的问题, 基于FPSO (Fuzzy PSO)算法来优化GT2FLC中的隶属函数参数, 从而增加GT2FLC的性能; 3) 通过仿真验证了GT2FLC相比于IT2FLC和T1FLC 具有更好的性能和处理不确定性的能力.

1. 电力巡检机器人

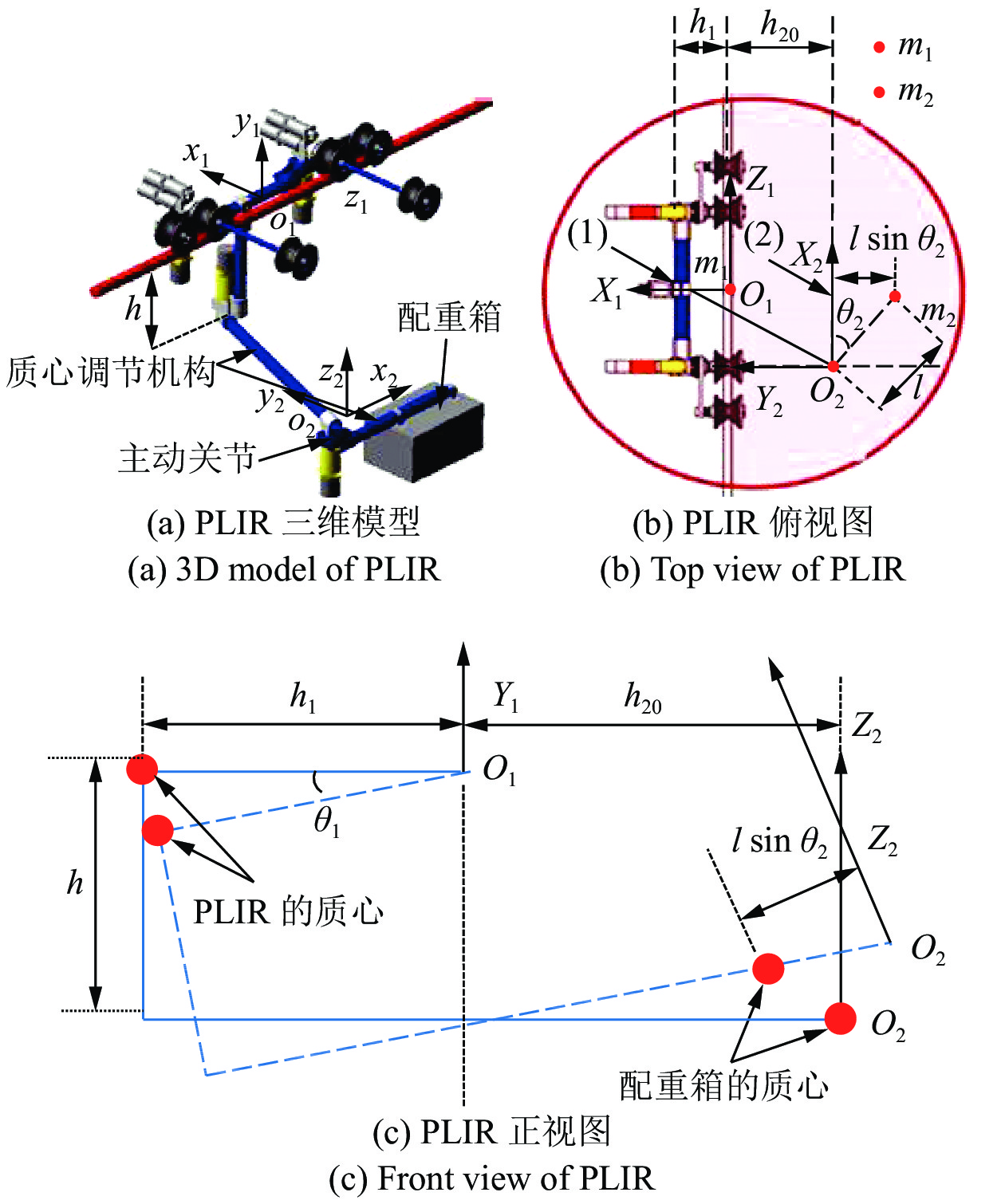
在本节中, 我们针对PLIR的工作原理进行介绍[1]. PLIR在高压输电线上作业时, 需要通过质心调节机构的调节来保持平衡, 其模型如图1所示. PLIR关于平衡调节的动力学方程可以通过欧拉−拉格朗日方程得到, 欧拉−拉格朗日方程表示为[42]

图 1 PLIR模型

Fig. 1 The model of PLIR

(1)

其中, $u_{i}$ 为作用在广义坐标的外部扭矩, $L$ 可以表示为

(2)

其中, $K$ 和 $P$ 分别表示机器人平衡调节模型的动能和势能, 可以表示为

(3)

(4)

其中, $θ_{1}$ 是PLIR与水平轴 $X_{1}$ 的倾角, 如图1所示; $θ_{2}$ 是执行器的杆旋转的角度; $m_{1}$ 和 $m_{2}$ 分别为机器人主体和配重箱的质量; $l$ 为执行器的杆的长度; $h$ 是 $T$ 型底座的高度; $h_{1}$ 为机器人平衡时, 配重箱的质心到高压输电线的距离; $h_{20}$ 为电线到机器人质心的距离; $g$ 是重力加速度. 以上各式中参数的值列在表1 中. 通过表1, 可知

(5)

将式(5)代入到式(4)中, 可得:

(6)

最终, 将式(3)和式(6)代入到式(1)中, 得到PLIR平衡调节的动力学方程, 表示为

(7)

其中, $u_{1}$ 是外部扰动, $u_{2}$ 是作用在关节上的扭矩. 对式(7)进行变换, 并且令 $[θ_{1}, {\dot{θ}}_{1}, θ_{2}, {\dot{θ}}_{2}]^{T} = [q_{1}, q_{2}, q_{3}, q_{4}]^{T}$ , 可得PLIR 平衡调节的状态空间模型为

(8)

表 1 PLIR对应参数值

Table 1 Values of parameters for the PLI robot

参数	参数值	参数	参数值
$m_{1} (k g)$	63	$m_{2} (k g)$	27
$h_{1} (m)$	0.18	$h_{20} (m)$	0.42
$l (m)$	0.5	$h (m)$	0.5

在本文中, $u_{2}$ 是GT2FLC的控制输出, 我们通过控制 $u_{2}$ 来对PLIR的平衡进行调节, 使得 $θ_{1}$ 稳定在平衡点附近. $u_{2}$ 不能直接调节 $θ_{1}$ , 而是通过系统的耦合性来间接地调整 $θ_{1}$ .

2. 广义二型模糊逻辑系统

2.1 广义二型模糊集

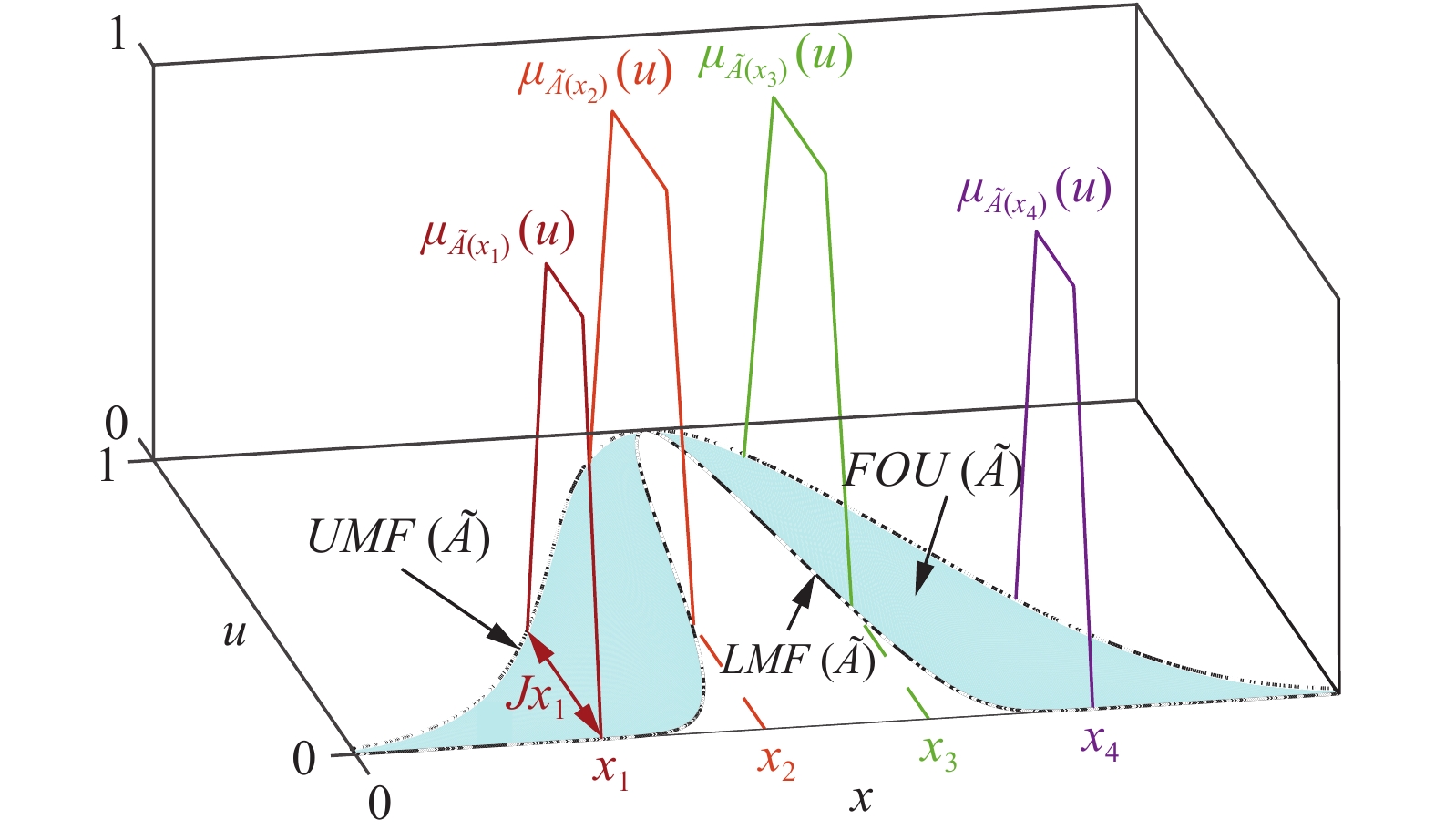
一个GT2FS记为 $\tilde{A}$ , 它的三维结构的隶属函数如图2所示. 一个GT2FS可以表示为

(9)

其中, $μ_{\tilde{A}} (x, u)$ 为次隶属度, $X$ 是主变量 $x$ 的定义域. 次隶属度的支撑域称为不确定性的迹(Footprint of uncertainty, FOU), 记为 $F O U (\tilde{A})$ , 即

(10)

图 2 广义二型模糊集

Fig. 2 General type-2 fuzzy set

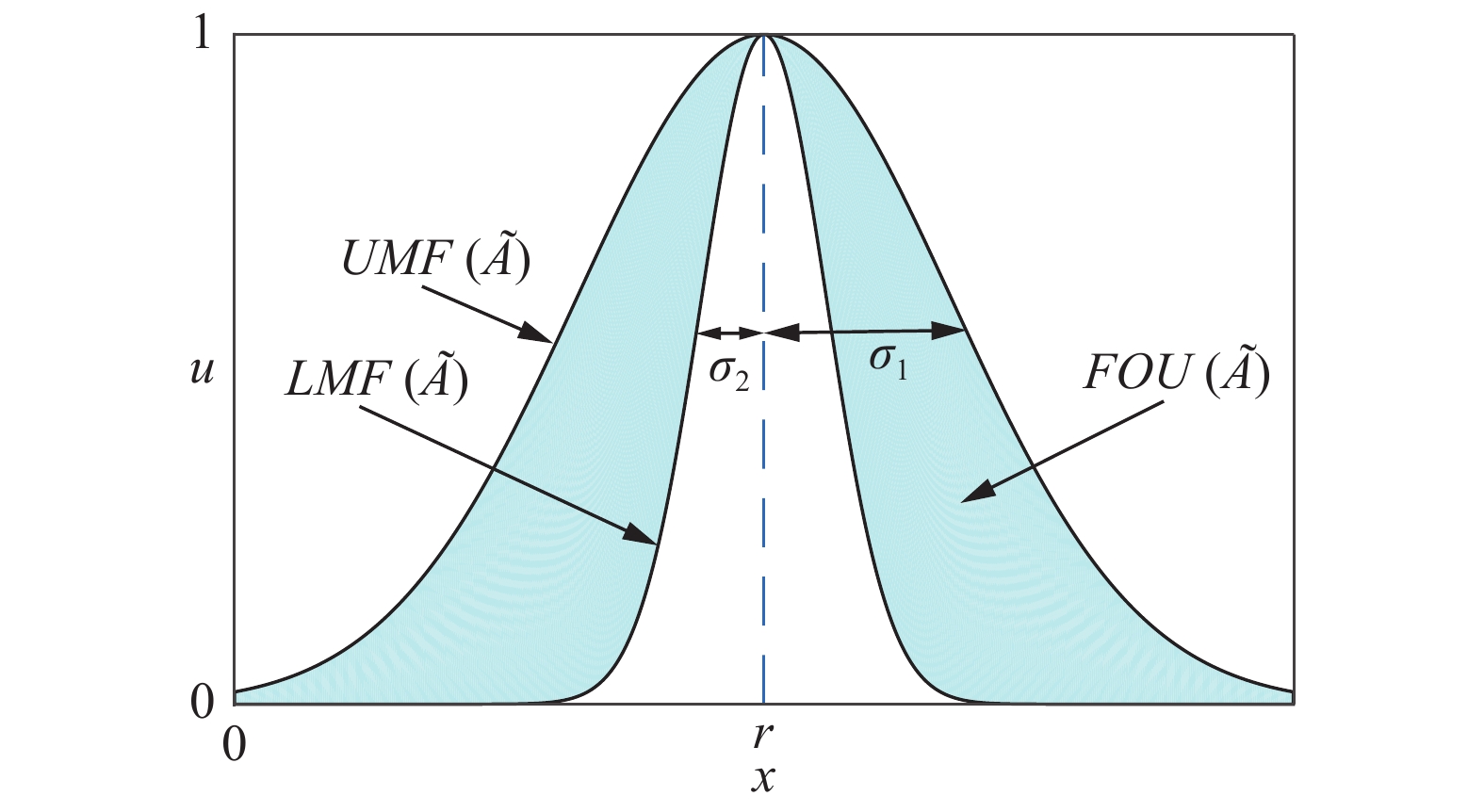
如图3所示, FOU被它的上、下隶属函数所包含. 其上、下隶属函数分别为 $U M F (\tilde{A})$ 和 $L M F (\tilde{A})$ , 即

(11)

(12)

图 3 不确定的迹

Fig. 3 The footprint of uncertain

为了使GT2FS的表示更加简便, 文献[26]提出了GT2FS的垂直切片表示法

A ~ = \int x \in X A ~ ( x ) x

(13)

(14)

其中, $\tilde{A} (x)$ 为次隶属函数; $μ_{\tilde{A} (x)} (u)$ 为次隶属度; $J_{x}$ 为主隶属函数, 同时也是次隶属函数的定义域. 次隶属函数本身是一个一型模糊集, 当次隶度 $μ_{\tilde{A} (x)} (u)$ 恒为1的时候, GT2FS就可以看成是一个区间二型模糊集.

Mendel等[30]通过 $α$ 平面来表示GT2FS, ${\tilde{A}}_{α} (x)$ 为 $μ_{\tilde{A} (x)} (u)$ 的 $α$ 截集, 即

(15)

GT2FS的一个 $α$ 平面为 ${\tilde{A}}_{α}$ , 即

(16)

最终, 一个GT2FS可以看作是 $α$ 平面的并集, 即

(17)

在 $\tilde{A}$ 中, 每一个 $α$ 平面都是一个区间二型模糊集. 通过多个 $α$ 平面来表示GT2FS, 可将GT2FS的运算转化为区间二型模糊集的运算. 特别地, 当 $α = 0$ 时的 $α$ 平面为 ${\tilde{A}}_{0}$ , 即

(18)

2.2 广义二型模糊逻辑控制器

一个GT2FLC由模糊器、模糊推理机、规则库、降型器、解模糊器这五个部分组成. 模糊器通过隶属函数, 能将精确的输入量映射到模糊空间中, 成为输入的GT2FS. 输入的GT2FS按照规则库中的模糊规则, 在推理机中通过模糊逻辑原理得到输出的GT2FS. 输出的GT2FS经过降型器和解模糊器得到精确的输出量.

在GT2FLC中, 隶属函数的上、下隶属函数通常为三角型、高斯和梯型, 次隶属函数通常为梯形、三角型和梯形. 规则库中的规则一般通过专家知识建立的, 一般用IF-THEN语句来表示. 在控制系统中有 $I$ 个输入和 $N$ 条规则, 那么第 $n$ 条规则具有如下的形式:

(19)

其中, ${\tilde{F}}_{i}^{n} (i = 1, 2, \dots, I)$ 是与输入 $x_{i} (i = 1, 2, \dots, I)$ 对应的GT2FS, 也称为前件; ${\tilde{G}}^{n}$ 是GT2FLC的后件, $y$ 是GT2FLC的最终输出. 模糊逻辑控制器中的IF-THEN规则是通过自然语言来描述的, 更容易让人接受. 模糊推理机一般为乘积推理机和最小推理机. 对于输入向量 $x = (x_{1}, x_{2}, \dots, x_{I})$ , 经过乘积推理, 得到在 $α$ 平面上的激活区间为 $[{\underline{f}}_{α}^{n}, {\bar{f}}_{α}^{n}]$ , 即

(20)

(21)

其中, ${\bar{μ}}_{α {\tilde{F}}_{i}^{n}} (x_{i})$ 和 ${\underline{μ}}_{α {\tilde{F}}_{i}^{n}} (x_{i})$ 分别为 $x_{i}$ 在 ${\tilde{F}}_{i}^{n}$ 中对应 $α$ 平面的上、下隶属度. 在模糊推理机中, 每条规则的输出都是一个GT2FS. 降型器只存在于二型模糊逻辑控制器中, 将二型模糊集转化为一型模糊集. 降型器与解模糊器有时可以看作是一个整体. 在本文中, 为了使得运算更加简便, 采用的是Biglarbegian-Melek-Mendel直接解模糊法[43]:

(22)

其中, ${\bar{y}}_{α}^{n}$ 和 ${\underline{y}}_{α}^{n}$ 为后件, $o$ 和 $p$ 要满足 $o + p = 1$ 的条件. 最后, 通过全局解模糊得到最终的输出值 $y$ , 即

(23)

其中, $α = {0, 1 / G, \dots, (G - 1) / G, 1}$ , $G$ 为广义二型模糊集被分割的次数, 一个GT2FS 集共有 $G + 1$ 个 $α$ 平面, $y$ 作为GT2FLC的输出作用到被控系统中.

3. 模糊粒子群优化算法原理

3.1 标准粒子群优化算法

在标准PSO算法中, 对于一个 $N$ 维的优化问题而言, 假设有 $M$ 个粒子, 每个粒子都是优化问题的一个潜在解, 在 $t$ 时刻, 记第 $i$ 个粒子的位置为 $X_{i} (t)$ , 第 $i$ 个粒子的速度为 $V_{i} (t)$ , 而第 $i$ 个粒子当前最优位置为 $P b e s t_{i} (t)$ , 可以表示为

(24)

其中, $f i t (P b e s t_{i} (t - 1))$ 和 $f i t (X_{i} (t))$ 为第 $i$ 个粒子相对应位置的适应值. 对于整个粒子群, 有一个最优的位置 $G b e s t (t)$ , 表示为

(25)

G b e s t (t) = P b e s t b (t)

(26)

在标准PSO中, 第 $i$ 个粒子通过式(12)来更新自己下一时刻的速度, 即

(27)

其中, $ω$ 为惯性权重, $c_{1}$ 表示认知因子, 代表粒子向自身最优值移动的加速权重; $c_{2}$ 表示社会因子, 代表粒子向全局最优值移动的加速权重; $r_{1}$ 和 $r_{2}$ 为0到1之间的随机变量. 在粒子更新速度的时候, 速度要在一定的范围内, 即

(28)

其中, $V_{m i n}$ 和 $V_{m a x}$ 为粒子速度的最小值和最大值. 通过式(14), 第 $i$ 个粒子更新自己下一时刻的位置, 即

(29)

在粒子更新位置, 位置要在一定的范围内, 即

(30)

其中, $X_{m i n}$ 和 $X_{m a x}$ 为粒子位置的最小值和最大值. 粒子需要不断地迭代来更新自己的位置, 直到达到终止条件为止. 终止条件一般为达到最大迭代次数或者是全局最优的适应值满足要求.

3.2 模糊粒子群算法(FPSO)

在FPSO中, 通过一个一型模糊逻辑系统(Type-1 fuzzy logic system, T1FLS)来调整惯性权重的值. 在算法迭代前期, 惯性权重取较大值, 使得粒子具有更好的全局搜索能力, 反之, 在算法迭代后期, 惯性权重取较小值, 使得粒子具有更好的局部搜索能力.

当前迭代次数 $i t e$ 和全局最优位置的适应值 $f i t (G b e s t)$ 作为模糊系统两个输入的信息, 在输入之前对其进行归一化处理, 即

N i t e = i t e i t e m a x

(31)

(32)

其中, $i t e_{m a x}$ 为最大迭代次数; $f i t_{m a x}$ 和 $f i t_{m i n}$ 分别为适应值的最大值和最小值.两个输入分别划分成5个一型模糊集: $N B$ 表示负大集, $N S$ 表示负小集, $Z O$ 表示零集, $P S$ 表示正小集, $P B$ 表示正大集, 它们的隶属函数如图4和图5所示. 这个T1FLS具有25条规则, 如表2所示. 最终, 惯性权重 $ω$ 通过式(33)计算得到[41]

图 4 Nite对应的隶属函数

Fig. 4 The membership function for Nite

图 5 Nfit对应的隶属函数

Fig. 5 The membership function for Nfit

(33)

(34)

其中, $y^{n}$ 为T1FLS后件集; $μ_{F_{1}^{n}} (N i t e)$ 和 $μ_{F_{2}^{n}} (N f i t)$ 为输入对应一型模糊集的隶属度. 通过T1FLS不断地更新FPSO中的惯性权重 $ω$ .

表 2 FPSO惯性权重调整模糊规则表

Table 2 The rulebase of adjustment for inertia weight in FPSO

$ω$		$N i t e$
$ω$		NB	NS	ZO	PS	PB
$N f i t$	NB	ZO	PS	PS	PB	PB
	NS	NS	ZO	PS	PB	PB
	ZO	NS	NS	ZO	PS	PS
	PS	NB	NB	NS	ZO	PS
	PB	NB	NB	NS	NS	ZO

4. 广义二型模糊控制器设计与优化

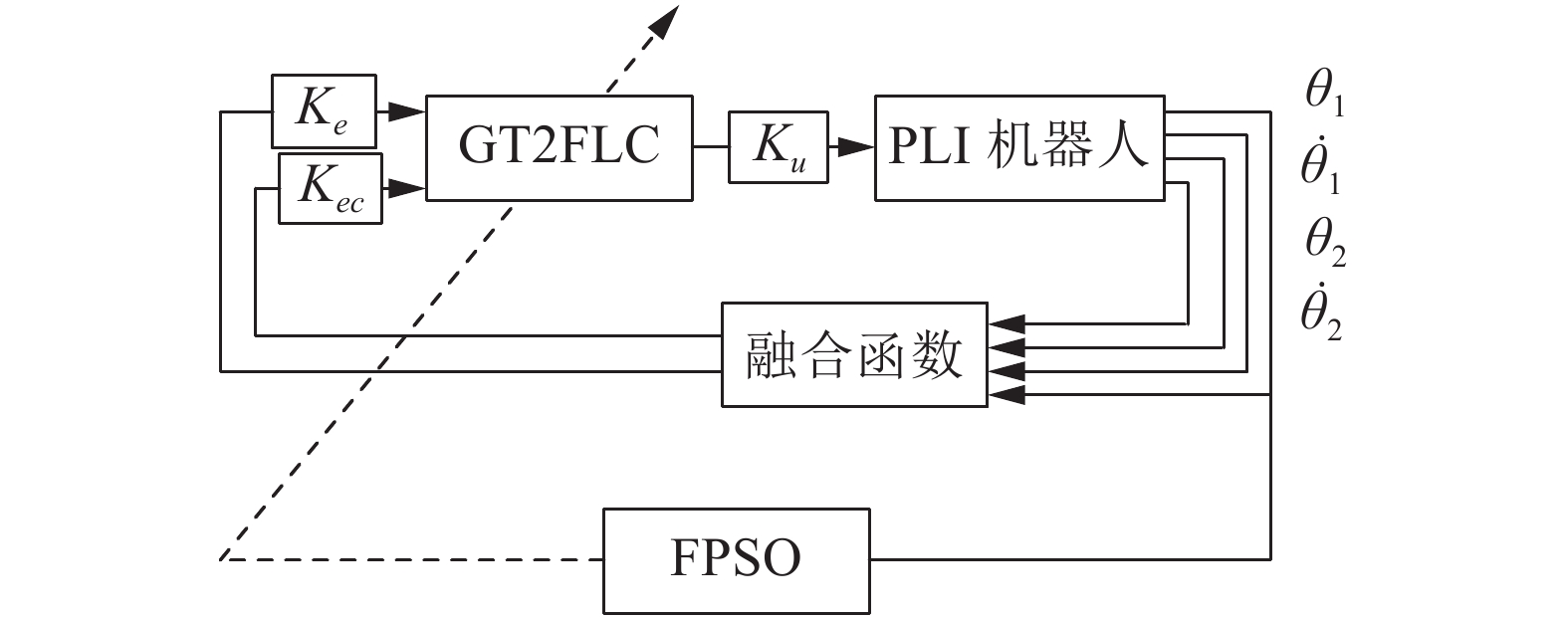
本节针对PLIR平衡调节的问题, 设计了一个GT2FLC. 基于FPSO算法, 对GT2FLC的隶属函数参数进行优化, 使得控制性能增强. 图6为电力巡检机器人的平衡控制优化的原理图.

图 6 PLIR平衡控制和优化原理图

Fig. 6 The diagram of balance control and optimization for the PLIR

4.1 广义二型模糊逻辑控制器设计

我们将PLIR的4 个状态变量 $[θ_{1}, {\dot{θ}}_{1}, θ_{2}, {\dot{θ}}_{2}]$ 作为反馈输入到GT2FLC 中. 为了避免反馈状态变量过多而导致的模糊规则爆炸, 将4 个状态变量通过信息融合的方法融合成2 个状态变量[44], 即

(35)

其中, $k$ 为状态反馈增益矩阵, 可以通过线性二次规划的方法得到; $[{\tilde{θ}}_{1} {\dot{\tilde{θ}}}_{1}]^{T}$ 为融合后的新的状态变量. 我们将 $[θ_{1} {\dot{θ}}_{1}]^{T}$ 作为融合的主变量, 融合后的新变量与主变量具有相同的物理意义. PLIR的整个控制流程如图6所示. $K_{e}$ 和 $K_{e c}$ 为量化因子, 可以将输入量从物理论域按比例转化到模糊论域中. $K_{u}$ 为比例因子, 可以将输出量从模糊论域转化到物理论域.

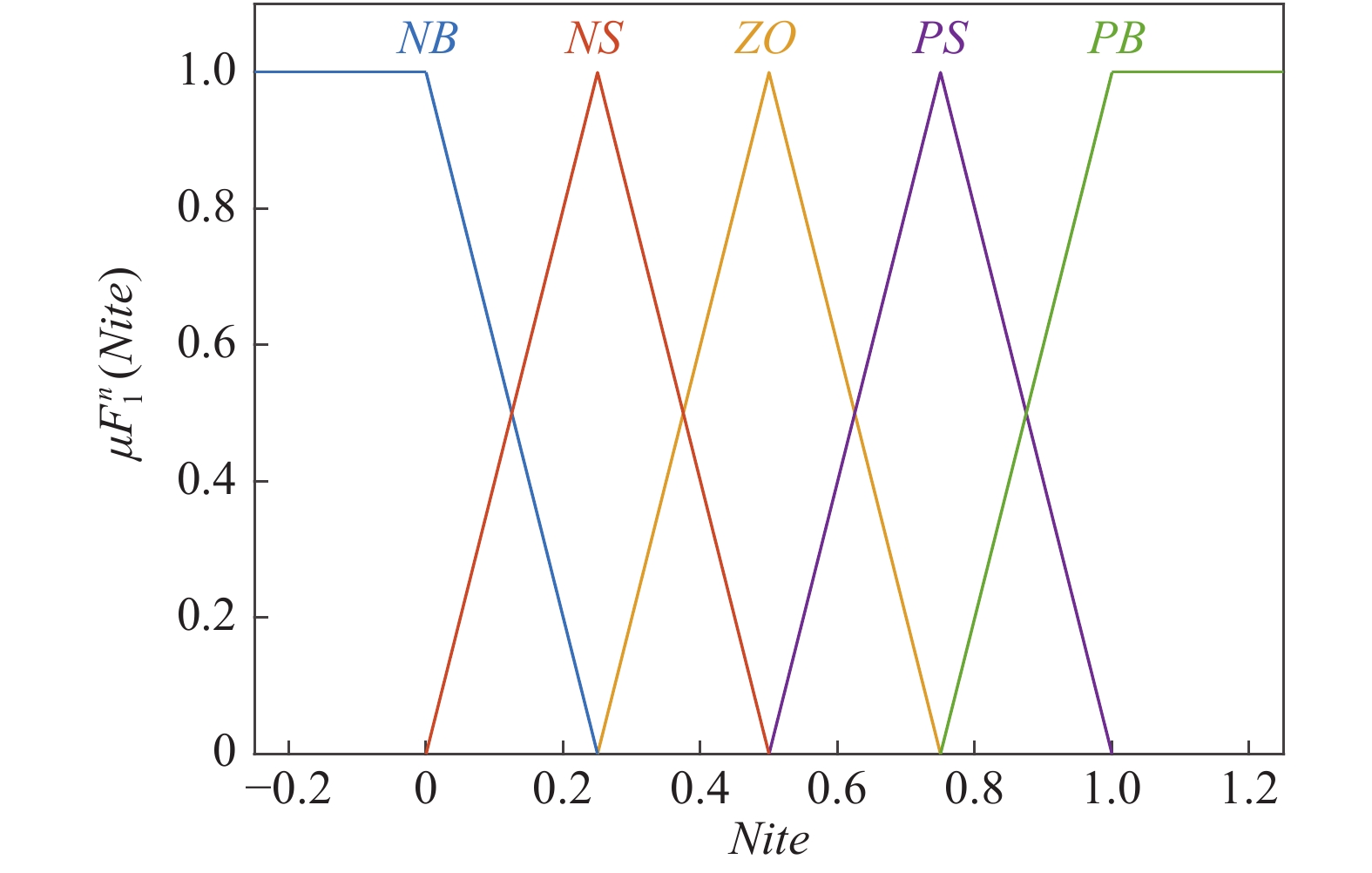
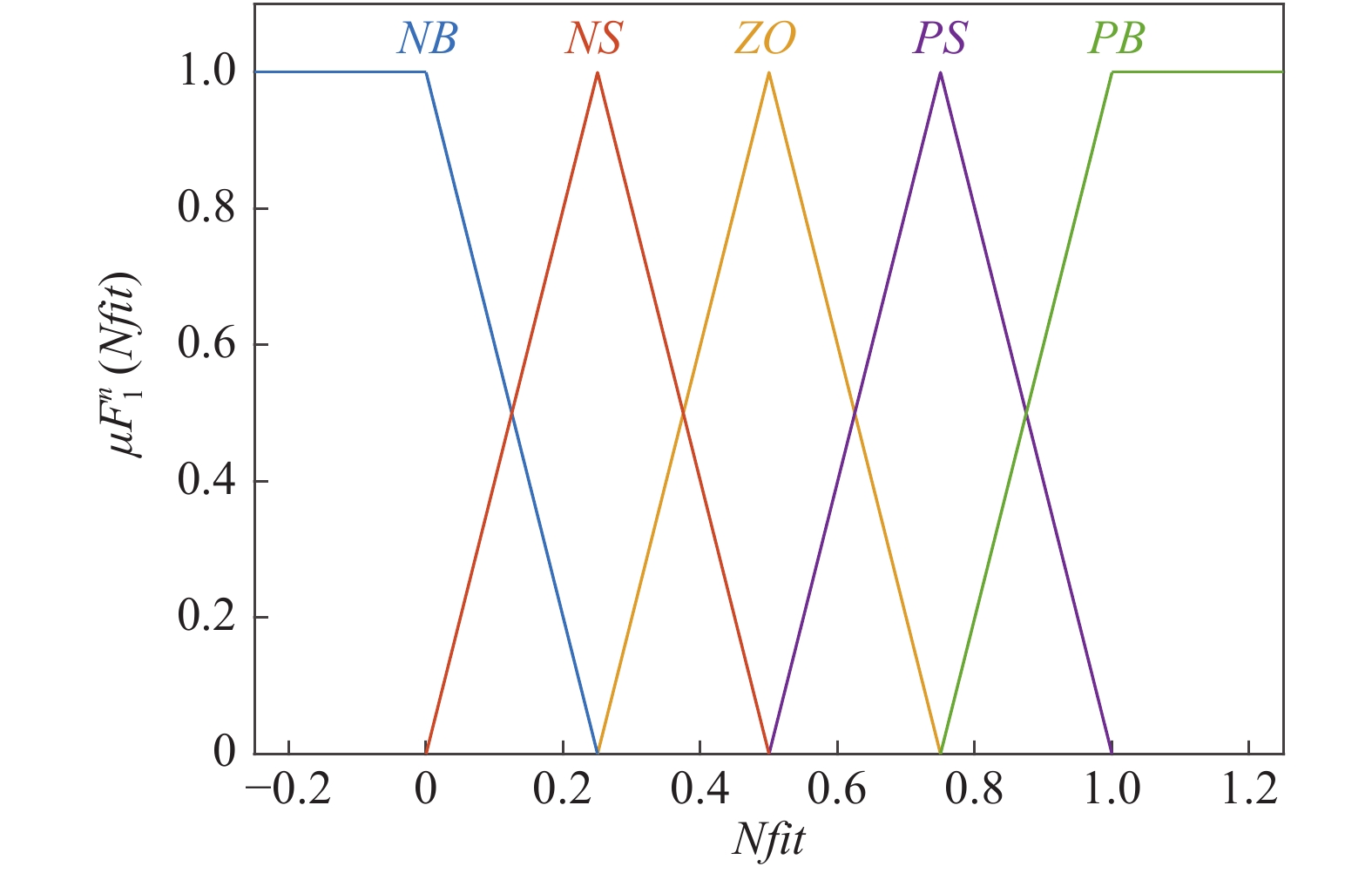
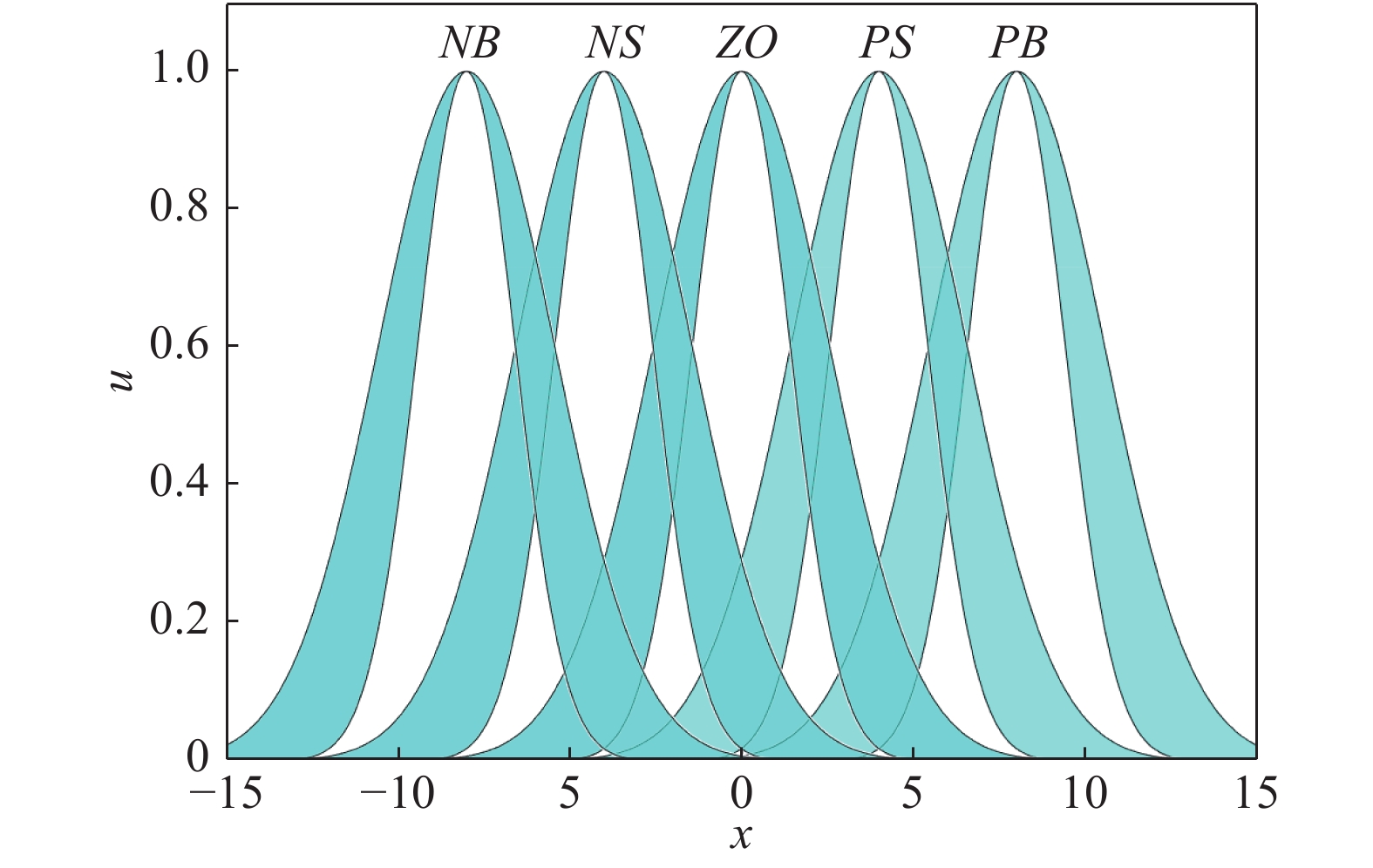
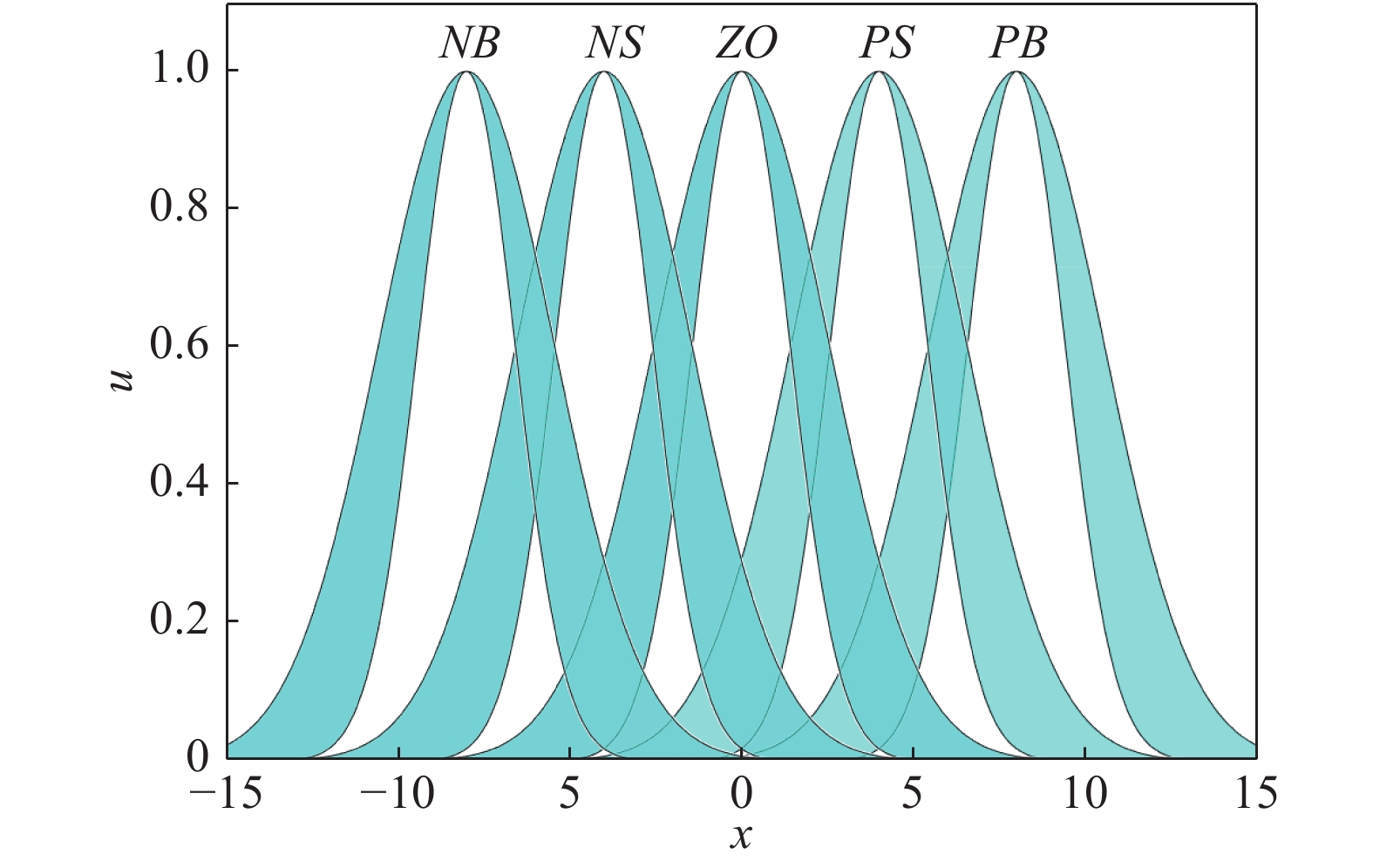
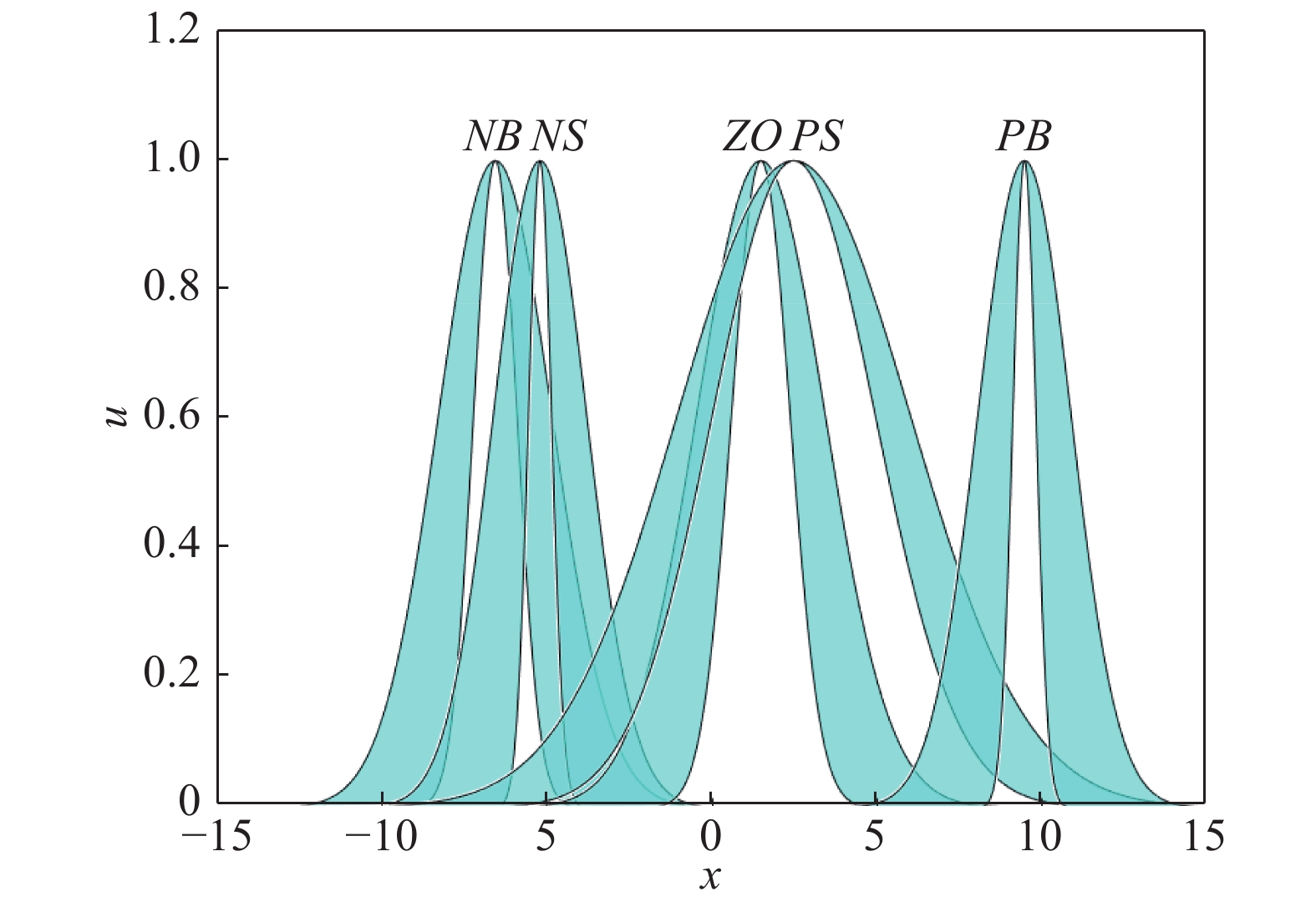
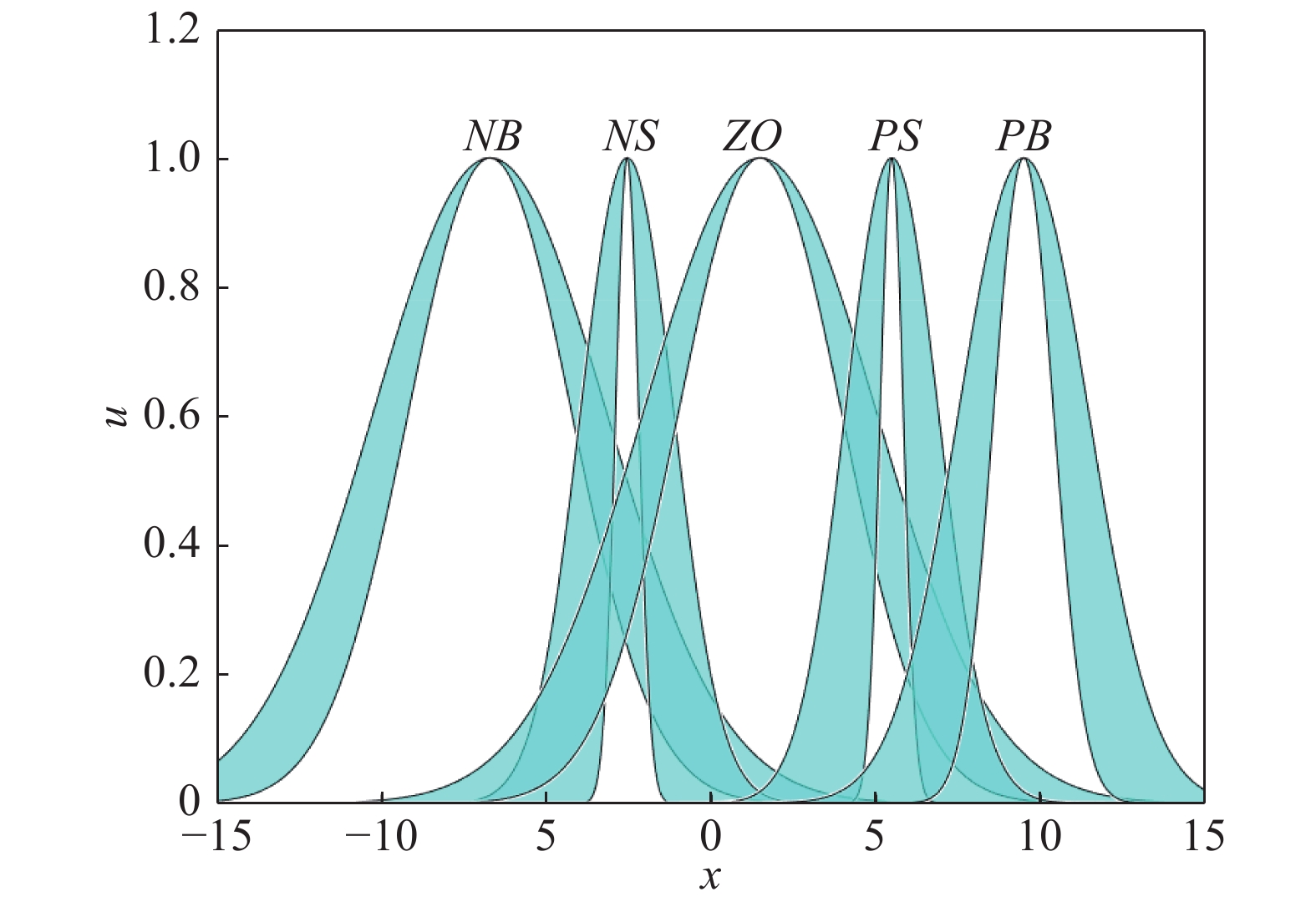
在本文中, 我们用5个GT2FS来对输入的模糊论域进行分割, 分别为负大集 $N B,$ 负小集 $N S,$ 零集 $Z O,$ 正小集 $P S,$ 正大集 $P B .$ 相应的主隶属函数为高斯型. 对于一个GT2FS, ${\underline{μ}}_{0 F_{i}^{n}} (x_{i})$ 和 ${\bar{μ}}_{0 F_{i}^{n}} (x_{i})$ 分别为 $F O U$ 平面上的上、下隶属度值, 即

(36)

(37)

其中, $r$ 为上、下隶属函数的均值; $σ_{1}$ 和 $σ_{2}$ 分别为上、下隶属函数的标准差. 次隶属函数选择为梯形, 其对应 $α$ 平面的次隶属度为

(38)

(39)

其中, $γ$ 决定次隶属函数形状的参数. 特别地, 当 $γ = 0$ 时, 次隶属函数为正方型, GT2FS 转化为一个区间二型模糊集. GT2FLC的模糊规则如表3所示.

表 3 PLIR平衡调节模糊规则表

Table 3 The rulebase of balance adjustment for the PLIR

u2		${\tilde{θ}}_{1}$
u2		NB	NS	ZO	PS	PB
${\dot{\tilde{θ}}}_{1}$	NB	PB	PB	PS	PS	ZO
	NS	PB	PB	PS	ZO	NS
	ZO	PS	PS	ZO	NS	NS
	PS	PS	ZO	NS	NB	NB
	PB	ZO	NS	NS	NB	NB

4.2 广义二型隶属函数优化

在本文中, 通过FPSO算法对GT2FLC的隶属函数进行优化, 以得到更好的控制性能. GT2FLC的两个输入分别对应5 个GT2FS, 而每个GT2FS的隶属函数需要用 $r$ , $δ_{1}$ , $δ_{2}$ , $γ$ 这4 个参数来表示, 所以FPSO中每个粒子都具有40 个维度. FPSO算法的适应度函数为平均绝对误差, 即

(40)

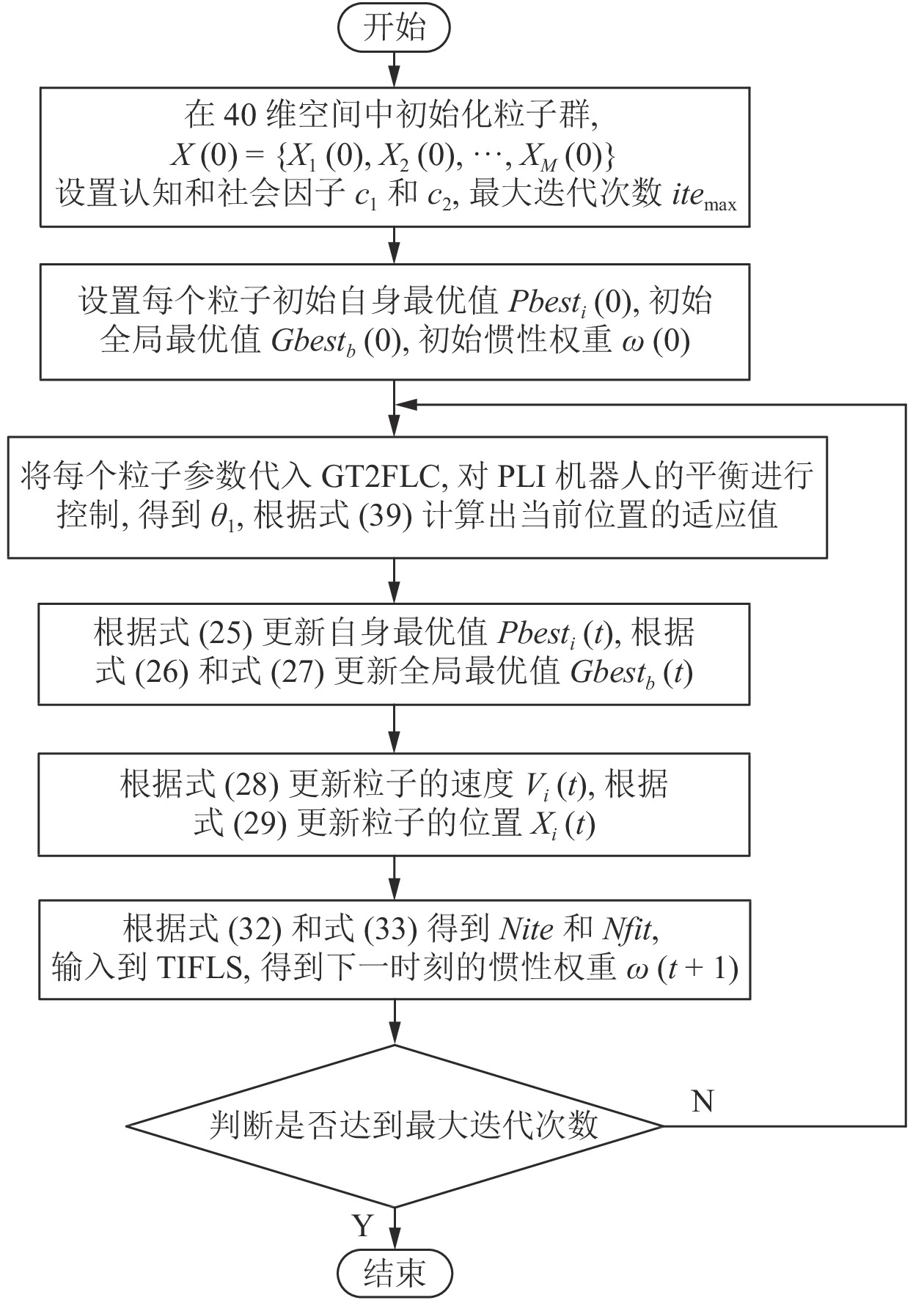
图7为整个FPSO的算法流程图. 最大迭代次数 $i t e_{m a x}$ 设为1 500, 种群数为50, $c_{1}$ 和 $c_{2}$ 为1.75. 本文相对文献[34], 通过T1FLS自适应动态更新PSO算法的参数, 可以搜索出更佳的GTFLC 的调节参数, 从而对PLIR实现更优控制。

图 7 FPSO算法流程图

Fig. 7 The flow diagram of the FPSO algorithm

5. 仿真结果与分析

本节针对PLIR平衡调节的非线性模型, 运用本文所设计的GT2FLC进行平衡控制, 并且通过FPSO算法对GT2FLC 中隶属函数参数进行优化. 同时, 本文还考虑了外部扰动对控制效果的影响. 此外, 为了验证本文方法的优越性, 设计了T1FLC和IT2FLC控制PLI机器人的平衡来与GT2FLC作对比. 最后将标准PSO算法与FPSO算法进行了对比. 图8和图9为GT2FLC两个输入优化前的隶属函数的FOU, 次隶属函数参数 $γ$ 都为0.5. 图10和图11为GT2FLC两个输入优化后的的隶属函数的FOU, 它的 $γ$ 的值分别为0.59, 0.28, 0.27, 0.65, 0.77, 0.54, 0.47, 0.27, 0.48, 0.63.

图 8 优化前

{\tilde{θ}}_{1}

对应的FOU

Fig. 8 The FOU for

{\tilde{θ}}_{1}

without optimization

图 9 优化前

{\dot{\tilde{θ}}}_{2}

对应的FOU

Fig. 9 FOU for

{\dot{\tilde{θ}}}_{2}

without optimization

图 10 优化后

{\tilde{θ}}_{1}

对应的FOU

Fig. 10 The FOU for

{\tilde{θ}}_{1}

with optimization

图 11 优化后

{\dot{\tilde{θ}}}_{2}

对应的FOU

Fig. 11 The FOU for

{\dot{\tilde{θ}}}_{2}

with optimization

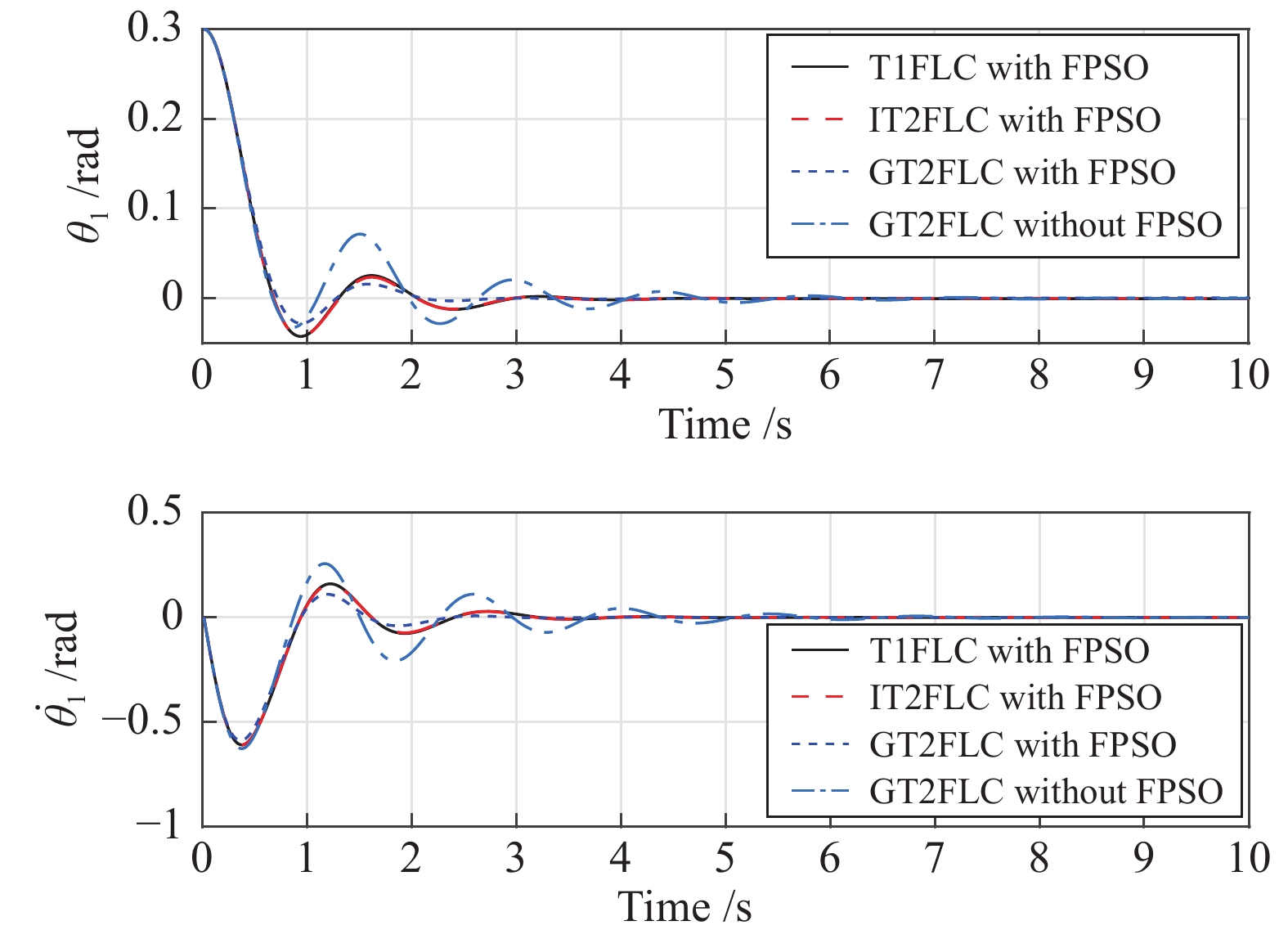
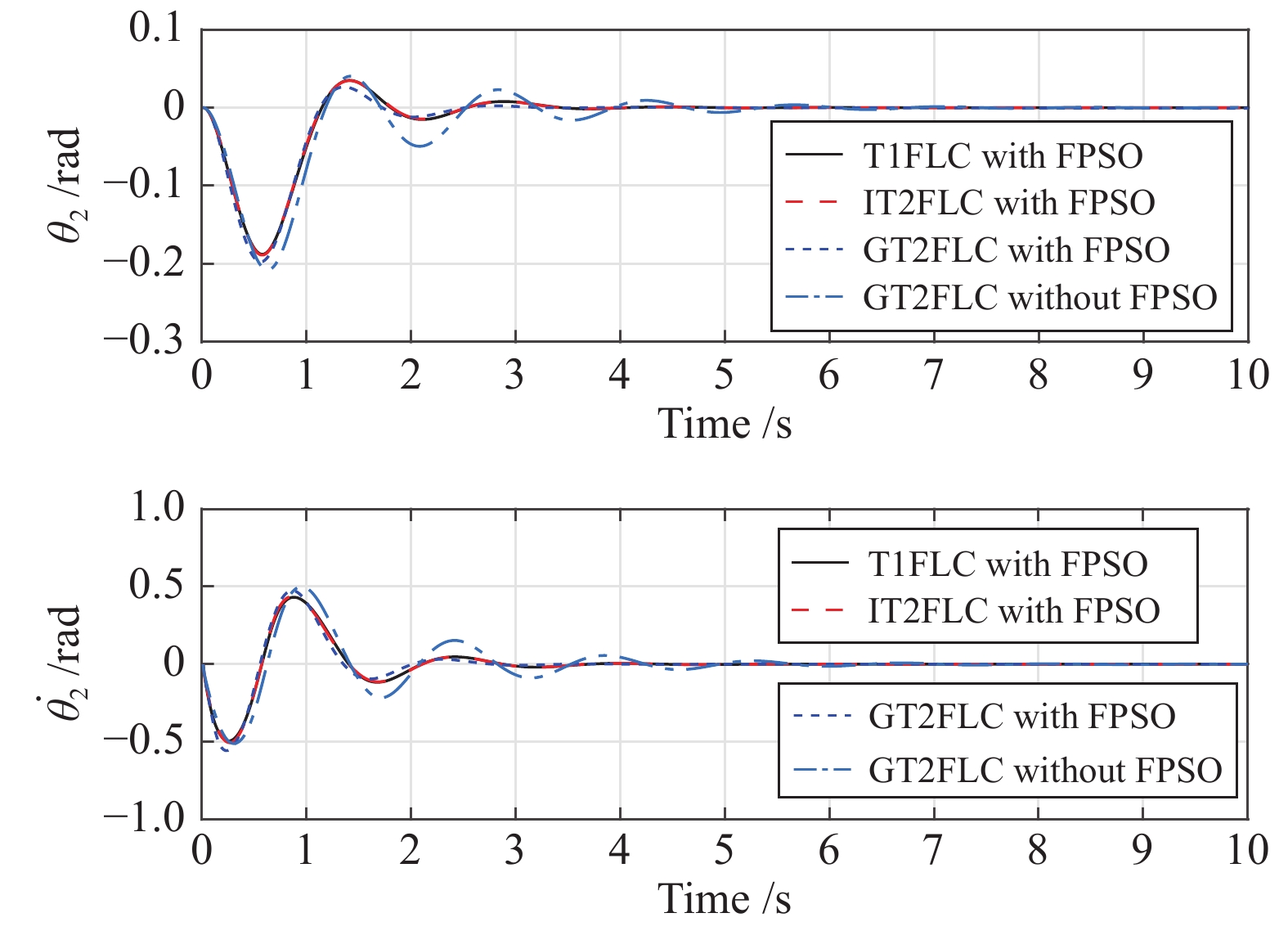
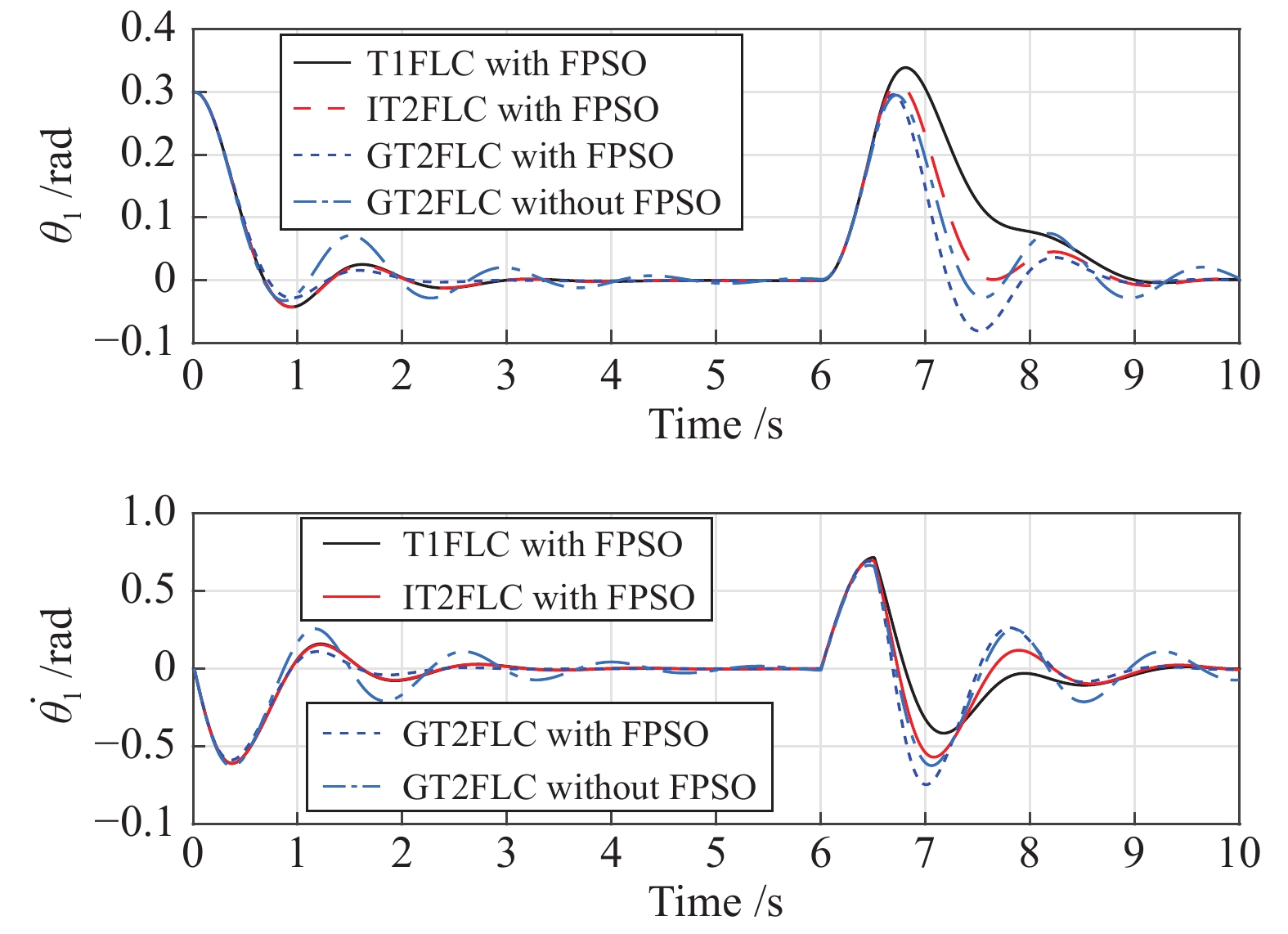
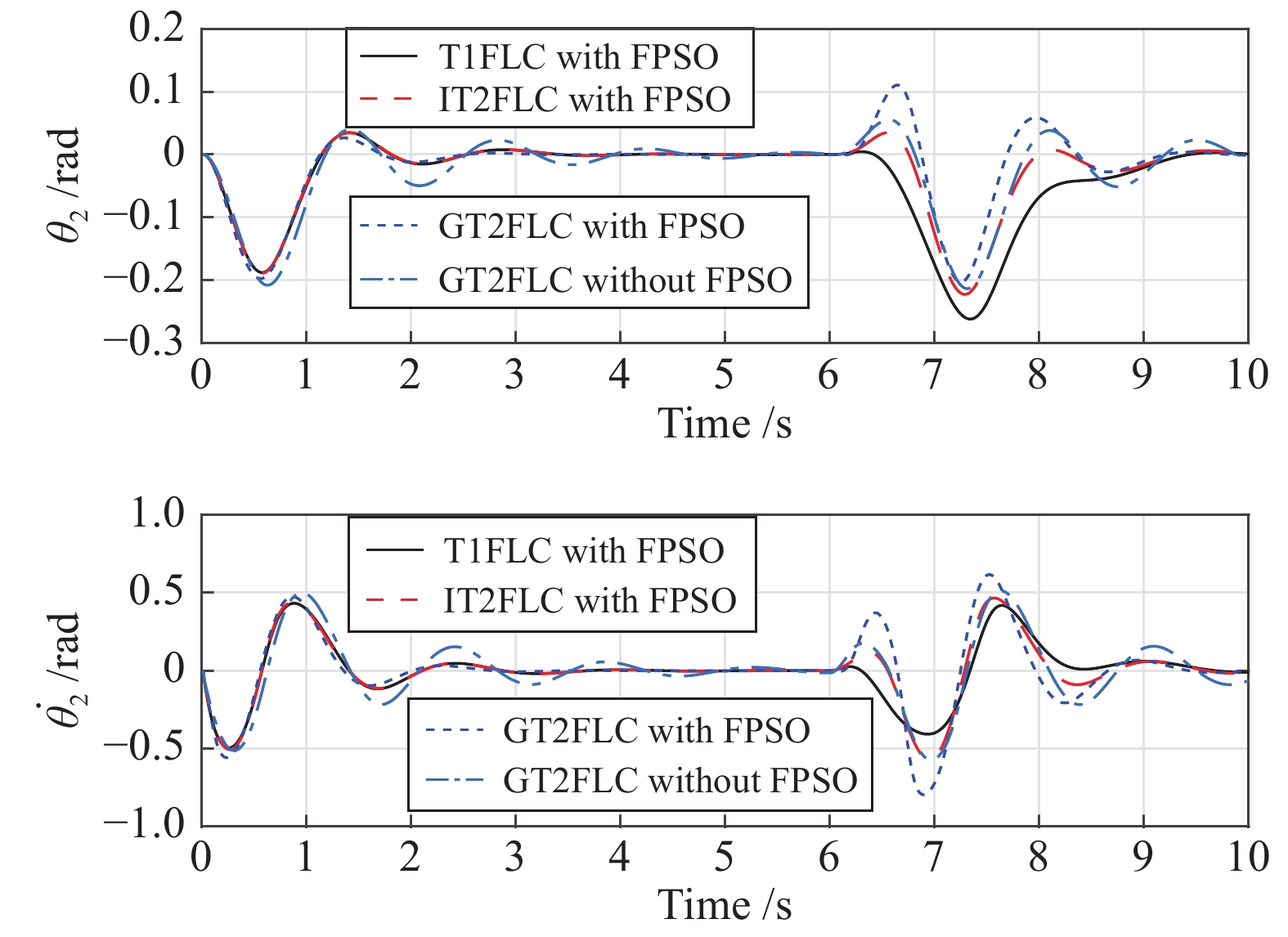
首先考虑在没有任何外部干扰的情况下, 对比在FPSO优化下的GT2FLC与没有优化的GT2FLC的平衡控制效果, 此外, 还与FPSO优化下的IT2FLC和T1FLC平衡控制效果进行了对比. 初始状态 $[θ_{1}, {\dot{θ}}_{1},$ $θ_{2}, {\dot{θ}}_{2}] = [0.3, 0, 0, 0]$ . 图12和图13 为PLIR四个状态的响应, 可以看出, 经过FPSO优化后的GT2FLC能使PLIR中的 $θ_{1}$ 到达平衡点位置后具有更小的超调, 并且振荡更小. 除此之外, 优化后的GT2FLC也比同样经过优化的IT2FLC和T1FLC具有更好的性能.

图 12 无干扰下

θ_{1}

和

{\dot{θ}}_{1}

的响应

Fig. 12 Responses of

θ_{1}

and

{\dot{θ}}_{1}

without disturbance

图 13 无干扰下

θ_{2}

和

{\dot{θ}}_{2}

的响应

Fig. 13 Responses of

θ_{2}

and

{\dot{θ}}_{2}

without disturbance

接下来考虑在有干扰情况下, 将几种控制器的控制效果作对比. 当PLIR机器人达到平衡时, 遇到一个外部干扰 $u_{1} = 30 N$ , 干扰持续0.5 s. 图14和图15为在干扰下PLIR的四个状态的响应. 显然, 两个GT2FLC相比于T1FLC和IT2FLC具有更好的处理不确定性的能力. TIFLC在遇到干扰后回到平衡位置速度最慢.

图 14 有干扰下

θ_{1}

和

{\dot{θ}}_{1}

的响应

Fig. 14 Responses of

θ_{1}

and

{\dot{θ}}_{1}

with disturbances

图 15 有干扰下

θ_{2}

和

{\dot{θ}}_{2}

的响应

Fig. 15 Responses of

θ_{2}

and

{\dot{θ}}_{2}

with disturbances

为了验真FPSO算法的优越性, 我们用标准PSO算法和FPSO算法分别对几种控制器进行30 次优化. 将两种优化算法优化后的控制器分别对两种情况下的PLIR机器人进行平衡控制, 因为 $θ_{1}$ 代表PLIR与水平轴的夹角, 所以我们通过评价函数对 $θ_{1}$ 进行计算来量化控制效果. 评价函数分别为平方误差积分(Integral square error, ISE)、误差绝对值积分(Integral absolute error, IAE)、时间乘以误差绝对值积分(Integral time absolute error, ITAE)

(41)

评价指标越小表明控制器具有越好的性能. 表4为几种控制器在无干扰情况下的评价指标的均值, 表5 为几种控制器在有外部干扰情况下的评价指标的均值. 可以看出, 在相同控制器之间进行对比, FPSO优化后的评价指标要比标准PSO优化的评价指标更小.

表 4 无干扰下平均评价指标

Table 4 Average evaluation index without disturbance

控制器	ISE	IAE	ITAE
T1FLC-PSO	0.02660	0.14820	0.08061
IT2FLC-PSO	0.02655	0.14238	0.06800
GT2FLC-PSO	0.02655	0.14290	0.06914
T1FLC-FPSO	0.02656	0.14534	0.07417
IT2FLC-FPSO	0.02653	0.14236	0.06732
GT2FLC-FPSO	0.02654	0.14127	0.06536

表 5 有干扰下平均评价指标

Table 5 Average evaluation index with disturbances

控制器	ISE	IAE	ITAE
T1FLC-PSO	0.07380	0.39140	1.76303
IT2FLC-PSO	0.06907	0.37776	1.69851
GT2FLC-PSO	0.06856	0.37537	1.68996
T1FLC-FPSO	0.07376	0.38991	1.75956
IT2FLC-FPSO	0.06875	0.37773	1.69275
GT2FLC-FPSO	0.06857	0.37414	1.68423

6. 结束语

本文针对PLIR平衡调节问题, 设计了一个GT2FLC, 并且通过FPSO算法优化了GT2FLC中的隶属函数参数. 仿真结果表明, GT2FLC经过FPSO算法的优化, 使PLIR更快地到达稳定位置, 并且具有更小的超调. 通过与IT2FLC 和T1FLC的对比表明, 本文所设计的GT2FLC有更好的控制效果. 在标准PSO与FPSO 的对比中, 可以看出经过改进后的FSO具有更好寻优能力. 在GT2FLC中, 隶属函数对控制性能具有很大的影响, GT2FS 三维结构的隶属函数相比于IT2FS与T1FS有更多的自由度, 使得GT2FLC具有比T1FLC和IT2FLC更大潜力. 在未来的工作中, 主要是通过三维仿真平台对本文的算法进行仿真, 以验证本文所提算法的有效性。

关键字：优秀论文

上一篇：一致性约束下末制导系统最大可容许模式决策延迟
下一篇：技术锁定对创新绩效的影响：创新模式的调节作用

栏目分类

热门排行

推荐信息

期刊知识