CO2混合工质的气液相平衡的混合规则对比与预测研究

引言

二氧化碳(CO2)属于自然工质，由于其高热稳定性、安全环保并且高能量密度实现部件小型化等优点，使得CO2动力循环在新一代热功转化循环、内燃机余热、中低温热能、火电、核电和太阳能利用等领域具有广泛的应用前景。同时CO2作为循环介质，也是一种对CO2的直接资源化利用方式，符合国家双碳政策，但是CO2纯工质循环运行压力高，应用中存在安全隐患，且临界温度较低对冷源要求很高[1]。碳氢类(HCs)工质虽能提高能源利用效率，但HCs易燃易爆；氢氟烃类工质(HFCs)的全球变暖潜能值（GWP）偏高，不符合《〈蒙特利尔议定书〉基加利修正案》的要求[2]；氢氟烯烃类工质(HFOs)汽化潜热低，热力性能较差。因此很难找到性能优异、热稳定性高又对环境友好安全的纯工质，而CO2混合工质动力循环通过不同的组分配比，可以实现既能提高能源利用效率又能对环境友好的要求。CO2+HCs混合工质可以消除可燃性，降低易燃易爆的风险；CO2+HFCs混合工质可以降低GWP值；CO2+HFOs混合工质可以提高工质的热力性能。

Bell等[3]总结了目前能作为制冷工质的各类混合工质的气液相平衡实验数据，其中CO2混合工质的气液相平衡实验数据有21种。混合工质气液相平衡理论计算的重点是选择合适的混合规则，提高计算精度，混合规则的形式各种各样，包括vdW混合规则、WS混合规则、MHV1混合规则等。各类CO2混合工质适用于何种混合规则没有明确给出，Kim等[4]对于CO2+propane混合工质使用vdW混合规则计算；对于CO2+HFC-134a混合工质，Duran-Valencia等[5]使用vdW混合规则计算气液相平衡数据，而Lim等[6]和Silva-Oliver等[7]选择的是WS混合规则；Valtz等[8-9]选择WS混合规则计算了CO2+HFC-152a和CO2+HFC-227ea的气液相平衡数据；对于CO2+HFO-1234yf混合工质，Juntarachat等[10]使用vdW混合规则计算气液相平衡数据；而Wang等[11]使用了WS混合规则计算了CO2+HFO-1234ze(E)混合工质。综上所述，目前各类CO2混合工质使用的混合规则形式不统一，系统分析不同混合规则形式对于各类CO2混合工质的适用性具有重要意义。另外，由于气液相平衡实验需要耗费大量的时间和精力，因此提出适合CO2混合工质气液相平衡的预测模型，也是一项具有重大意义的工作。

本文结合CO2混合工质动力循环的应用背景，选取出11种 CO2混合工质的气液相平衡实验数据，包括7种CO2+HFCs/HFOs二元体系和4种 CO2+HCs二元体系。选用PR方程结合三种不同形式的混合规则(vdW、WS、MHV1)计算这11种二元体系的气液相平衡数据，并与各体系公开发表的文献实验值相比较，得出计算结果与实验数据之间的相对偏差，从而分析与讨论不同混合规则对于各类CO2混合工质的适用性。最后提出一种差值模型，对CO2混合工质气液相平衡模型进行了预测。

1 气液相平衡的理论基础公式

气液相平衡性质反映的是流体气液两相之间的相互关系，描述的是混合物气液平衡时，其温度T、压力p和气相组分yi 、液相组分xi 之间的关系。气液相平衡理论需要状态方程结合混合规则与活度系数模型描述得出。

1.1 PR状态方程

本文采用PR方程作为计算混合工质气液相平衡的基础。PR方程由Peng和Robinson在1976年提出[12]，其表达式为：

p=RTv−b−av(v+b)+b(v−b)$p=\frac{RT}{v-b}-\frac{a}{v(v+b)+b(v-b)}$(1)

式中，a$a$和b$b$是状态方程系数，可由临界参数和偏心因子计算得到：

a=0.45724R2T2cpcα(T)$a=0.45724\frac{R^2{T}_c^2}{p_c}\alpha \left(T\right)$(2)b=0.0778RTcpcα(T)$b=0.0778\frac{R{T}_c}{p_c}\alpha \left(T\right)$(3)

α(T)$\alpha \left(T\right)$函数定义为：

α(T)=[1+(0.37646+1.54226ω−0.26992ω)(1−T0.5r)]22$\alpha \left(T\right)=[1+(0.37646+1.54226\omega -0.26992\omega {}_{}{}^2\left)\right(1-T{}_r^{0.5}){]}^2$(4)

状态方程被用于描述混合工质的热力学性质时，需要引入混合规则。

1.2 混合规则

1.2.1 vdW混合规则

描述混合工质的热力学性质时，vdW[13]混合规则被广泛应用，作为一种常数型混合规则，其形式如下：

am=∑i∑jxixjaij$a_m=\sum _i\sum _j{x}_i{x}_j{a}_{ij}$(5)bm=∑ixibi$b_m=\sum _i{x}_i{b}_i$(6)aij=aiaj−−−−√(1−kij)$a_{ij}=\sqrt[]{a_i{a}_j}(1-k_{ij})$(7)

1.2.2 MHV1混合规则

MHV1混合规则是Michelsen[14]对HV[15]混合规则进行改进得到的，其是一种经典的GE-EOS混合规则, 以零压为参考态，具体形式如下：

ambmRT=∑ixiaibiRT+1q1O$\frac{a_m}{b_{m}RT}=\sum _i{x}_i\frac{a_i}{b_{i}RT}+\frac{1}{q_1}O$(8)bm=∑ixibi$b_m=\sum _i{x}_i{b}_i$(9)O=GERT+∑ixiln(bmbi)$O=\frac{G^E}{RT}+\sum _i{x}_{i}ln\left(\frac{b_m}{b_i}\right)$(10)

1.2.3 WS混合规则

Wong和Sandler于1992年提出Wong-Sandler(WS)混合规则[16]，该法则基于超额Helmholtz自由能，与密度无关且满足第二维里系数边界条件, 其形式如下：

bm=∑i∑jxixj(b−aRT)ij1−GECRT−∑ixi(aiRTbi)$b_m=\frac{\sum _i\sum _j{x}_i{x}_j{\left(b-\frac{a}{RT}\right)}_{ij}}{1-\frac{G^E}{CRT}-\sum _i{x}_i\left(\frac{a_i}{RT{b}_i}\right)}$(11)(b−aRT)ij=12[(b−aRT)i+(b−aRT)j](1−kij)${\left(b-\frac{a}{RT}\right)}_{ij}=\frac{1}{2}\left({\left(b-\frac{a}{RT}\right)}_i+{\left(b-\frac{a}{RT}\right)}_j\right)(1-k_{ij})$(12)ambm=∑ixiaibi+GEC$\frac{a_m}{b_m}=\sum _i{x}_i\frac{a_i}{b_i}+\frac{G^E}{C}$(13)

三种混合规则各有优势，WS和MHV1混合规则对高度非理性体系和强极性体系有着非常好的描述能力；而vdW混合规则只有一个交互参数，形式简单，具有较强的物理意义。

1.3 活度系数模型

1968年Renon和Prausnitz[17]修正了溶液局部组成表达式, 在双流体理论的基础上提出了NRTL活度系数模型,其能很好地描述二元体系的相平衡性质, 对于常见的二元系统其表达式为:

GERT=x1x2(τ21G21x1+x2G21+τ12G12x1+x1G12)$\frac{G^E}{RT}=x_1{x}_2\left(\frac{{\tau }_{21}{G}_{21}}{x_1+x_2{G}_{21}}+\frac{{\tau }_{12}{G}_{12}}{x_1+x_1{G}_{12}}\right)$(14)G12=exp(−α12τ12),G21=exp(−α21τ21)$G_{12}=exp(-{\alpha }_{12}{\tau }_{12}),G_{21}=exp(-{\alpha }_{21}{\tau }_{21})$(15)

组分1、2的活度系数方程为:

lnγ1=x22[τ21G221(x1+x2G21)2+τ12G12(x2+x1G12)2]$ln{\gamma }_1=x_2^2\left(\frac{{\tau }_{21}{G}_{21}^2}{(x_1+x_2{G}_{21}{)}^2}+\frac{{\tau }_{12}{G}_{12}}{(x_2+x_1{G}_{12}{)}^2}\right)$(16)lnγ2=x21[τ12G212(x2+x1G12)2+τ21G21(x1+x2G21)2]$ln{\gamma }_2=x_1^2\left(\frac{{\tau }_{12}{G}_{12}^2}{(x_2+x_1{G}_{12}{)}^2}+\frac{{\tau }_{21}{G}_{21}}{(x_1+x_2{G}_{21}{)}^2}\right)$(17)

2 混合物气液相平衡计算

三种混合规则中的相互作用参数需要结合实验数据，使用目标函数优化计算得出。本文的目标函数综合考虑了压力计算相对偏差与气相组分浓度绝对偏差，如下所示：

OF=1N∑i=1N[(pexp−pcalpexp)2+(y1,exp−y1,cal)2]12$OF=\frac{1}{N}{\sum _{i=1}^N\left({\left(\frac{p_{exp}-p_{cal}}{p_{exp}}\right)}^2+{\left(y_{1,exp}-y_{1,cal}\right)}^2\right)}^{\frac{1}{2}}$(18)AARD(p)=1N∑i=1N∣∣pexp−pcalpexp∣∣×100%$AARD\left(p\right)=\frac{1}{N}\sum _{i=1}^N\left(\frac{p_{exp}-p_{cal}}{p_{exp}}\right)\times 100\%$(19)AAD(y)=1N∑i=1N∣∣y1,exp−y1,cal∣∣$AAD\left(y\right)=\frac{1}{N}\sum _{i=1}^N\left(y_{1,exp}-y_{1,cal}\right)$(20)

本文分别在CO2/HFCs、CO2/HFOs和CO2/HCs二元体系中选取了CO2(1)+HFC-152a(2)[9]、CO2+HFO-1234ze(E)[11]、CO2+propane[4]三类混合工质，给出了不同混合规则的比较。

2.1 CO2+HFC-152a混合工质各种混合规则对比

CO2(1)+ HFC-152a(2)混合工质的压力相对偏差、气相摩尔分数绝对偏差以及p-x-y曲线如图1、图2所示，其中图2中的散点表示不同温度下的气液相平衡的实验点，从图中可以看出对于CO2(1)+ HFC-152a(2)混合工质，WS+NRTL混合规则压力相对偏差的绝对值在1%以内，气相摩尔分数绝对偏差的绝对值在0.01以内，其计算精度最高；在低于CO2临界温度304.13 K的温区(亚临界区域)，三种混合规则计算精度相差不大，但在高于CO2临界温度的温区(超临界区域)，WS+NRTL混合规则的优势就体现了出来，这是因为WS混合规则对高度非理性体系和强极性体系有着非常好的描述能力。

图1

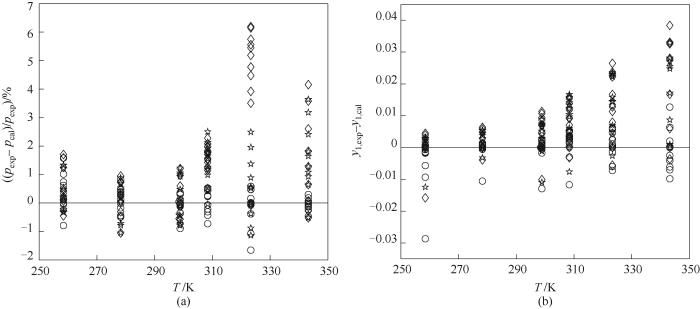
图1   CO2(1)+HFC-152a(2)的压力相对偏差与气相摩尔分数绝对偏差

○ WS+NRTL; ☆ MHV1+NRTL; ◇ vdW

Fig.1   The relative deviation of the pressure and the absolute deviation of the component mole fraction of CO2 (1) + HFC-152a (2)

图2

图2   CO2(1)+HFC-152a(2) 的 p-x-y曲线

─ WS+NRTL; ┄ MHV1+NRTL; … vdW; □ 实验数据点

Fig.2   p-x-y diagram of CO2(1)+HFC-152a(2)

2.2 CO2+HFO-1234ze（E）混合工质各种混合规则对比

从图3、图4中可以看出对于CO2(1)+HFO-1234ze(E)(2)混合工质，WS+NRTL混合规则效果最好，MHV1+NRTL次之，vdW最差；在低于CO2临界温度区域(亚临界区域)三种混合规则计算精度相差不大，但在高于CO2临界温度区域(超临界区域)，WS+NRTL混合规则的优势较高，MHV1+NRTL的计算精度也较高，误差较大的地方其实在液相区，这是因为对于MHV1混合规则，液相摩尔体积是一个恒定的常数导致的。

图3

图3   CO2(1)+HFO-1234ze(E)(2)的压力相对偏差与气相摩尔分数绝对偏差

○ WS+NRTL; ☆ MHV1+NRTL; ◇ vdW

Fig.3   The relative deviation of the pressure and the absolute deviation of the component mole fraction of CO2 (1) +HFO-1234ze(E) (2)

图4

图4   CO2(1)+HFO-1234ze(E)(2) 的 p-x-y曲线

─ WS+NRTL; ┄ MHV1+NRTL; … vdW; □ 实验数据点

Fig.4   p-x-y diagram of CO2(1)+HFO-1234ze(E)(2)

2.3 CO2+propane混合工质各种混合规则对比

从图5、图6中可以看出对于CO2(1)+ propane(2)混合工质，vdW混合规则的压力偏差和气相摩尔分数绝对偏差与WS和MHV1混合规则相差不大，甚至在高温区(高于CO2临界温度304.13 K)更具优势，此时vdW混合规则形式简单的优势突显出来，这是因为该二元体系非理想性不强导致的。本文后续会继续介绍CO2(1)+烷烃(2)混合工质使用vdW混合规则的优势，并通过已知温区下的二元交互作用参数推算未知温区下的二元交互作用参数，从而推算未知温区下的气液相平衡曲线。

图5

图5   CO2(1)+propane(2)的压力相对偏差与气相摩尔分数绝对偏差

○ WS+NRTL; ☆ MHV1+NRTL; ◇ vdW

Fig.5   The relative deviation of the pressure and the absolute deviation of the component mole fraction of CO2 (1) +propane (E) (2)

图6

图6   CO2(1)+propane(2) 的 p-x-y曲线

─ WS+NRTL; ┄ MHV1+NRTL; … vdW; □ 实验数据点

Fig.6   p-x-y diagram of CO2(1)+propane(2)

2.4 CO2混合工质各种混合规则对比

采用PR+WS+NRTL模型、PR+MHV1+NRTL模型和PR+vdW模型对7种CO2+HFCs/HFOs二元混合工质气液相平衡性质进行了计算。计算结果见表1，包括了实验点数和实验温区，采用PR+WS+NRTL模型，AARD(p)为0.61%，AAD(y)为0.0055；采用PR+MHV1+NRTL模型，AARD(p)为1.14%，AAD(y)为0.0091；采用PR+vdW模型，AARD(p)为1.41%，AAD(y)为0.0110。3种模型对比可知，对于CO2+HFCs/HFOs二元体系，相比于vdW混合规则，MHV1混合规则对计算精度提升有限，WS混合规则对计算精度提升明显。

表1   三种混合规则对CO2+HFCs/HFOs混合工质的气液相平衡计算偏差

Table 1  Calculation deviations in the vapor-liquid equilibrium of the CO2+HFCs/HFOs mixtures by three mixing rules

采用三种模型对4种CO2+HCs二元混合工质气液相平衡性质进行了计算。计算结果见表2，采用PR+WS+NRTL模型，AARD(p)为0.57%，AAD(y)为0.0060；采用PR+MHV1+NRTL模型，AARD(p)为0.73%，AAD(y)为0.0068；采用PR+vdW模型，AARD(p)为1.01%，AAD(y)为0.0066。3种模型对比可知，对于CO2+HCs二元混合工质，相比于vdW混合规则，MHV1与WS混合规则对计算精度提升有限，特别是对气相组分，计算精度基本没有提升。

表2   三种混合规则对CO2+HCs二元混合工质气液相平衡计算偏差

Table 2  Calculation deviations in the vapor-liquid equilibrium of the CO2+HCs mixtures by three mixing rules

对于CO2+烷烃类二元混合工质，在vdW混合规则下，利用实验数据回归计算各个温区下的k12如表3所示，从表中可以看出，CO2+propane[4]、CO2+n-butane[20-21]、CO2+isobutane[22-23]三种二元混合工质的二元交互作用参数k12都在0.12~0.13附近。将这些温区下的二元交互作用参数取平均值与先前优化出来的二元交互作用参数做对比，分别计算各个温区下的AARD(p)和AAD(y)的值，计算结果如表4所示。

表3   CO2+烷烃类混合工质的二元交互作用参数的最优值 （vdW混合规则）

Table 3  Optimal value of binary interaction parameters for CO2+alkane mixtures （vdW mixing rules）

表4   CO2+小分子烷烃二元混合物的优化结果与预测结果的比较

Table 4  Comparison of the optimization results and prediction results of CO2 + small molecule alkane binary mixture

2.5 CO2+小分子烷烃混合工质的气液相平衡的预测

从表4中可以看出，对于CO2+小分子烷烃体系，平均二元交互作用参数与优化的二元交互作用参数相比，计算精度相差不大。因此对于这类混合工质可以用平均二元交互作用参数代替使用实验数据优化的二元交互作用参数，并将这一结论扩展到其他没有计算的温区，利用平均二元交互作用参数得到的气液相平衡数据与实验值比较，如图7所示。

图7

图7   vdW混合规则预测的p-x-y曲线

Fig.7   p-x-y diagram predicted by vdW mixing rules

如图7所示，使用平均二元交互作用参数，计算330 K下的CO2+propane[26]、387 K下的CO2+n-butane[20]和320 K下的CO2+isobutane[27]，计算结果与实验点拟合较好，进一步验证了使用平均二元交互作用参数的有效性。这一发现具有重要的意义，对于CO2+小分子烷烃二元体系，通过少量的实验，得出二元交互作用参数的规律，预测没有实验数据的温区下的气液相平衡，可以节省大量实验所需要的时间与精力。

2.6 CO2+HFCs/HFOs混合工质的气液相平衡的预测

Hu等[28]指出，WS与MHV1这类多参数状态方程很难预测混合工质气液相平衡性质，然而如果状态方程中二元交互作用参数可以预测，则大大降低实验耗费的精力。表5列出了CO2+HFCs/HFOs二元体系，使用PR+vdW模型回归计算的各个温区下的k12的值。目前关于混合工质气液相平衡的预测主要集中在半经验公式的预测、基团贡献法的预测以及理论模型的预测。结合Hu等[28]、Chen等[29]、Zhang等[30]以及Duarte等[31]对二元交互作用参数k12的处理，由于CO2与含氟制冷剂的特殊性质，提出一种CO2与含氟制冷剂的差值计算模型[式(21)~式(23)]，结合CO2和制冷剂的物性参数以及氟原子数量，具有一定的物理意义。

k12=k1−k2$k_{12}=k_1-k_2$(21)k1=p0.5c,CO2ωCO2Tc,CO2+p0.25c,CO2n0.1FωCO2Tc,CO2$k_1=\frac{p_{c,C{O}_2}^{0.5}{\omega }_{C{O}_2}}{T_{c,C{O}_2}}+\frac{p_{c,C{O}_2}^{0.25}{n}_F^{0.1}}{{\omega }_{C{O}_2}{T}_{c,C{O}_2}}$(22)k2=p0.5c,CO2ωHFCs,HFOsTc,CO2+p0.25c,CO2n0.1FωHFCs,HFOsTc,CO2$k_2=\frac{p_{c,C{O}_2}^{0.5}{\omega }_{HFCs,HFOs}}{T_{c,C{O}_2}}+\frac{p_{c,C{O}_2}^{0.25}{n}_F^{0.1}}{{\omega }_{HFCs,HFOs}{T}_{c,C{O}_2}}$(23)

表5   CO2+HFCs/HFOs混合工质的二元交互作用参数的最优值 （vdW混合规则）

Table 5  Optimal value of binary interaction parameters for CO2+HFCs/HFOs （vdW mixing rules）

这个差值模型，只与CO2的临界温度、临界压力和偏心因子以及含氟制冷剂的偏心因子和氟原子数量有关，是一个完全预测性的模型。以该模型计算得到的二元交互作用参数与前面优化结果进行对比，计算结果如表6所示。

表6   CO2+HFCs/HFOs混合工质的优化结果与预测结果的比较

Table 6  Comparison of the optimization results and prediction results of CO2 +HFCs/HFOs

由表6可知，优化计算得到的AARD(p)值为1.17%，AAD(y)值为0.0078，而预测的AARD(p)值为2.03%，AAD(y)值为0.0120，所以可以看出该预测模型的精度很高。由于CO2+含氟制冷剂的气液相平衡实验数据较少，这一差值模型的提出对于处理其他没有实验数据的混合工质具有极其重要的意义。

3 结 论

本文将PR方程与vdW、MHV1、WS三种混合规则相结合，建立了CO2混合工质气液相平衡计算模型，计算了11种CO2混合工质的相平衡性质，包括7种CO2+HFCs/HFOs二元体系和4种 CO2/HCs二元体系。主要结论如下。

（1）对于CO2+HFCs/HFOs二元体系，相比于vdW混合规则，MHV1混合规则对计算精度提升有限，WS混合规则对计算精度提升明显，因此需要通过形式较为复杂的MHV1或WS混合规则对CO2+HFCs/HFOs的气液相平衡性质进行关联和预测。

（2）对于CO2+HCs二元体系，因HC分子极性弱于HFC和HFO，其二元混合物非理想性不强，因此相比于vdW混合规则，MHV1与WS混合规则对气液相平衡性质的计算精度提升有限，特别是对气相组分，计算精度基本没有提升。

（3）对于CO2+小分子烷烃二元体系，可以通过PR方程结合vdW混合规则，通过部分等温线下的实验数据获得平均二元交互作用参数，对于CO2+烷烃混合工质平均二元交互作用参数在0.12~0.13附近，可以通过平均二元交互作用参数对其他温区下的气液相平衡进行预测。

（4）对于CO2+含氟制冷剂二元体系，提出了一种差值模型预测其气液相平衡性质，预测得到的AARD(p)值为2.03%，AAD(y)值为0.0120，预测效果较好，下一阶段的研究目标是扩展这一差值模型的适用工质范围。

符 号 说 明