考虑输出约束的冗余驱动绳索并联机器人预设性能控制
并联机器人具有高精度、高刚度及大负载自重比等优点, 已大量应用于高速搬运、运动模拟与电子制造等行业. 绳索驱动并联机器人是传统刚性并联机器人的延伸, 它采用绳索取代传统刚性并联机器人的刚性杆件, 具有工作空间大、杆件惯性低、可扩展性强等优点[1].
然而, 由于绳索具有柔性仅能传递拉力, 因此必须保证绳索运行过程中始终处于拉伸状态, 目前通用的做法是增加冗余支链形成冗余驱动绳索并联机器人(Redundantly-actuated cable driving parallel robots, RCDPRs), 通过控制冗余系统内力实现各杆件拉伸进而保证机器人正常运行. 由于制造与安装误差的存在, 机器人杆件长度、驱动装置与负载安装位置、驱动系统与负载等参数都存在误差, 这将产生模型不确定性, 同时由于外部扰动的存在, 系统扰动项不可忽略. 开展冗余驱动绳索并联机器人高速高精度轨迹跟踪控制受到了广泛关注, 这也是目前的研究难点与热点. 动力学前馈控制[2]、神经网络控制[3]、鲁棒
由于滑模控制对参数不确定及外部扰动具有较强的鲁棒性及扰动抑制能力, 因此被广泛应用于线性与非线性系统控制中. 为提高传统线性滑模控制的收敛速度, 文献[8-9]在滑模面设计时采用非线性超平面代替传统滑模面中的线性超平面, 提出了终端滑模控制 (Terminal sliding mode control, TSMC)与快速终端滑模控制 (Fast terminal sliding mode control, FTSMC), 此类控制方法不仅具有有限时间收敛特性, 同时降低了控制增益, 然而跟踪误差在零附近时TSMC与FTSMC的控制输入将会出现奇异问题; 文献[10-13]通过设计滑模面中分数次幂项提出了非奇异终端滑模控制 (Nonsingular terminal sliding mode control, NTSMC)与非奇异快速终端滑模控制 (Nonsingular fast terminal sliding mode control, NFTSMC), 解决了TSMC与FTSMC中的奇异问题; 针对文献[12-13]中由于误差高阶项的非线性系数使得控制算法设计复杂的问题, 文献[14]提出在分段点具有两阶连续的NFTSMC算法. 然而, 采用上述算法取得的跟踪精度依赖于滑模面系数的选择, 较大的系数将会取得良好的跟踪精度, 但同时也需要更大的驱动力矩, 因此, 研究NFTSMC中滑模面系数的选择方法使得其可以依据跟踪误差数值进行调整具有重要意义.
符号函数的使用及其增益的过估计产生的抖振现象是滑模控制面临的另外一个关键问题. 为了降低或消除抖振问题, 国内外学者提出了边界层滑模、高阶滑模、自适应滑模与基于观测器的滑模控制等. 自适应滑模控制采用模糊规则、神经网络、多项式对扰动项进行逼近, 或对符号函数的增益项进行自适应更新, 并在算法稳定性分析时确定自适应项更新率, 进而保证算法稳定性[15-16]. 自适应方法可以获得较小的稳态跟踪误差, 但通常需要较大的增益才能取得理想效果, 同时需要较大驱动力矩. 基于观测器的滑模控制是解决抖振问题的另外一种有效方法, 该方法采用观测器对扰动项进行估计, 国内外研究学者分别采用了扰动观测器[17-18]、扩张观测器[19]、时延观测器[20]、滑模观测器[21]对滑模控制的扰动项进行估计, 但扰动估计精度依赖于观测器参数的选择. 模型不确定与扰动观测器 (Uncertainty and disturbance estimator, UDE)采用滤波器对扰动项进行估计, 目前已应用于机械系统控制的扰动估计中[22-24], 且与时延观测器相比, UDE可以取得更好的扰动估计效果[25]. 然而, UDE等扰动观测器通常被视为低通滤波器, 无法对高频扰动进行有效估计, 这将产生稳态跟踪误差, 且观测精度对参数选取较敏感.
上述研究仅考虑了稳态误差, 没有考虑系统整个运行阶段的输出约束. 现有针对输出约束的研究主要采用障碍Lyapunov函数与预设性能函数进行实现, 由于基于障碍Lyapunov函数的方法存在描述输出性能的参数少及内在奇异性问题, 使得其应用受到一定限制[26-27]; 基于预设性能的方法通过构建非线性函数将约束形式的跟踪误差转化为无约束形式变量, 同时可以通过设计指数衰减函数实现给定时间的输出约束[28-29], 该方法已被广泛应用于机器人控制中. 然而现有基于预设性能的输出约束控制主要采用指数衰减函数, 无法获得达到预定性能的具体时间, 同时由于机器人中电机与减速机输出能力不对称等原因, 研究非对称给定时间输出约束具有重要意义. 为实现冗余驱动绳索并联机器人的高精度控制并解决上述方法存在的问题, 本文将开展以下研究: 1) 设计给定时间衰减函数与非线性变换函数, 并将考虑预设性能的跟踪误差转换为无约束变量, 实现非对称给定时间输出约束; 2) 提出基于精度驱动且在分段点处三阶连续的非奇异快速终端滑模面进行控制算法设计, 实现有限时间控制; 3) 结合扰动观测器与自适应控制优点, 在预设性能控制中采用UDE进行扰动估计, 并通过自适应方法对扰动估计误差进行补偿, 同时开展仿真研究, 验证本文算法的有效性.
1. 动力学建模与问题描述
1.1 冗余驱动绳索并联机器人动力学建模
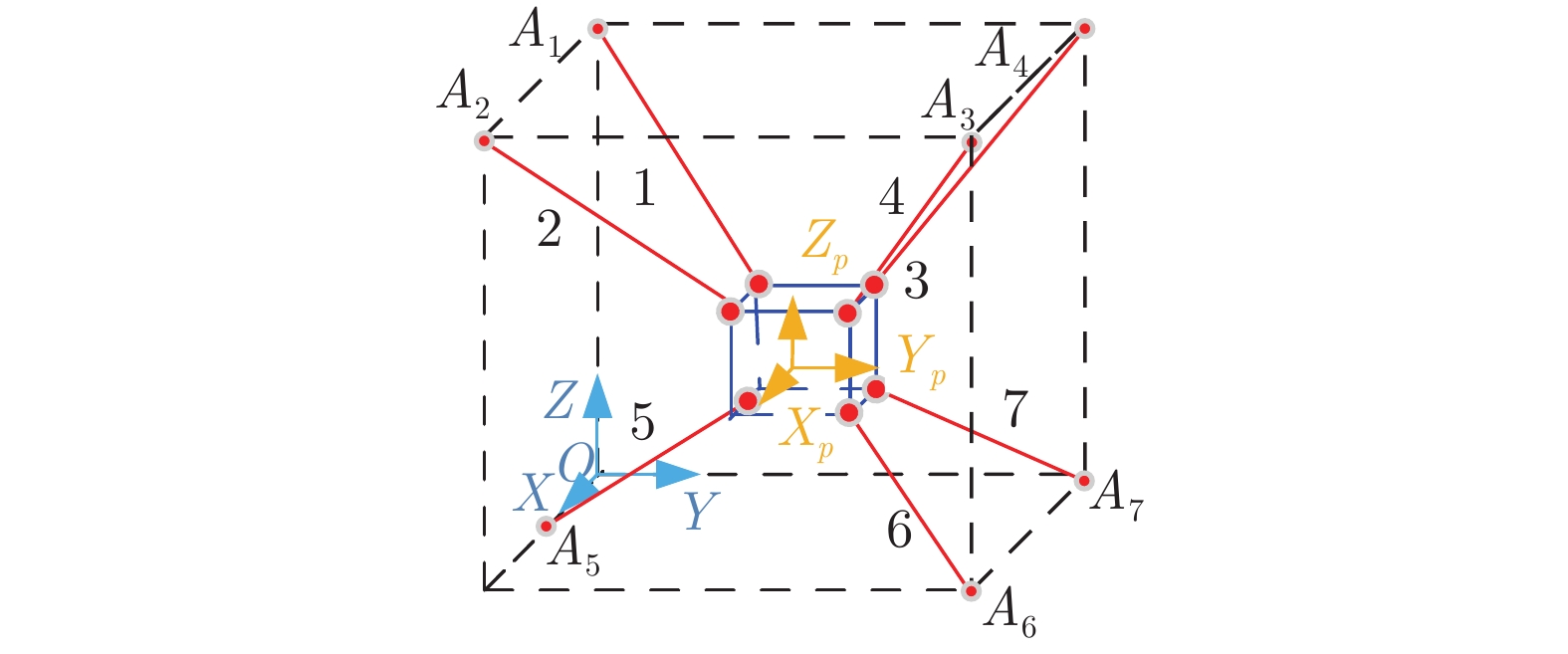
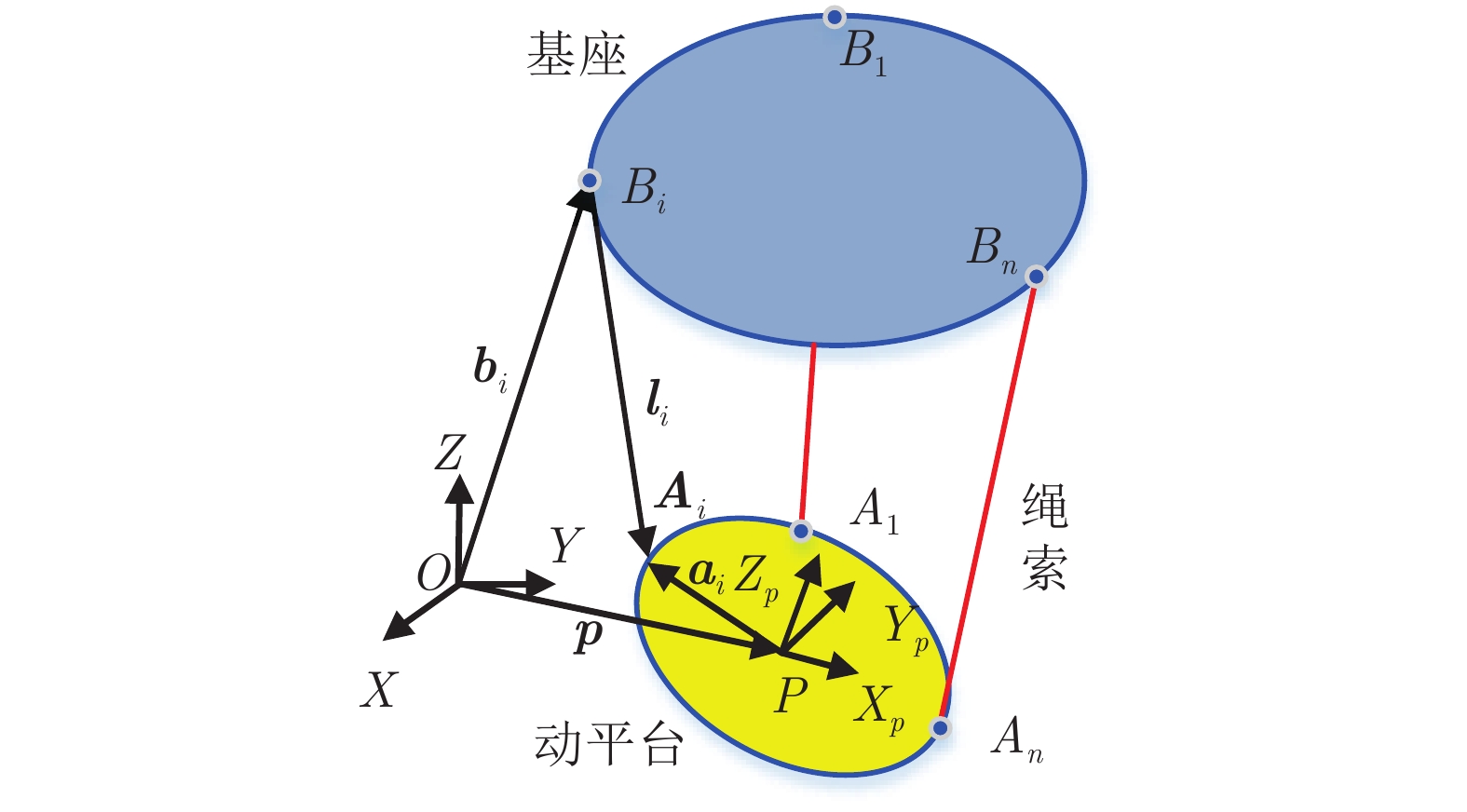
动力学模型是开展控制算法研究的基础, 本节以图1所示具有m个自由度的冗余驱动绳索并联机器人为对象分别开展运动学与动力学建模, 该机器人由基座、动平台和n条通过绳索连接的分支组成. 坐标系
| (1) |
其中,
根据图1, 绳索i的运动方程及长度可表示为[31]:
| (2) |
其中,
将式(2)第一部分对时间求一阶导数, 并对方程两边点乘
| (3) |
其中,
| (4) |
其中,
| (5) |
其中,
| (6) |
其中, mp为动平台质量,
| (7) |
根据牛顿运动定律, 电机运动方程为:
| (8) |
其中, Ib与r为电机−滑轮组件的转动惯量及滑轮半径,
| (9) |
将式(9)两边同时乘以
| (10) |
其中,
设置绳索组成的支链数n大于机器人自由度m, 因此可以在保证机器人正常运行的情况下控制绳索内力保证其拉伸状态. 根据式(7), 绳索拉力可表示为:
| (11) |
其中,
| (12) |
其中,
| (13) |
其中,
假设 1. 假设扰动项
1.2 问题描述
对于冗余驱动绳索并联机器人, 假设其末端位置
2. 控制算法设计与稳定性分析
引理 1[32]. 对于任意给定的正数
| (14) |
其中,
引理 2[33]. 对于连续正定函数
| (15) |
2.1 UDE方法
UDE方法根据系统模型、控制律及滤波器得到扰动表达式[34-35], 可表示为:
| (16) |
其中,
| (17) |
其中, s为Laplace算子,
| (18) |
定义
| (19) |
根据式(19)可得:
| (20) |
其中,
由于时间常数T是正值, A为Hurwitz矩阵. 根据假设1与式(20), 存在正向量
注 1. 对于冗余驱动绳索并联机器人系统, 模型不确定项
2.2 针对输出约束的非线性变换
根据动力学模型, 定义跟踪误差为:
| (21) |
其中,
| (22) |
其中,
| (23) |
其中,
式(22)为约束形式的跟踪误差
| (24) |
其中,
| (25) |
其中,
1)
转换后的跟踪误差
| (26) |
根据式(26), 跟踪误差
| (27) |
2.3 精度驱动滑模面设计
为保证跟踪误差有限时间收敛, 本文提出精度驱动的非奇异快速终端滑模面:
| (28) |
其中,
| (29) |
其中,
注 2. 式(29)中
引理 3. 根据式(28)所示滑模面, 构造如下系统:
| (30) |
其中,
证明. 考虑Lyapunov函数
| (31) |
由式(29), 当
| (32) |
根据引理1, 当
| (33) |
其中,
| (34) |
根据式(34), 当
| (35) |
□
2.4 基于UDE的自适应滑模控制算法设计
根据式(28), 滑模面的导数可表示为:
| (36) |
根据上式可定义控制律为:
| (37) |
其中,
| (38) |
扰动估计项可表示为:
| (39) |
鲁棒控制项可表示为:
| (40) |
其中,
| (41) |
注 3. 定义
为对扰动观测误差进行补偿, 选择
| (42) |
其中,
| (43) |
将式(37)代入式(43), 并结合式(38) ~ 式(40)可得到扰动估计值
| (44) |
2.5 算法收敛性证明
定理 1. 考虑系统模型(10)、扰动估计值(44)、控制律(38) ~ (40), 则滑模变量s与跟踪误差
证明. 该定理的证明分为2个步骤, 步骤1证明滑模面具有有限时间收敛特性, 步骤2分析位置跟踪误差
步骤 1. 为证明滑模面的收敛特性, 构造如下Lyapunov函数:
| (45) |
其中,
| (46) |
根据引理1, 并将式(41)代入式(46), 可得:
| (47) |
将自适应更新率(42)代入式(47)可得:
| (48) |
由杨氏不等式有
| (49) |
其中,
| (50) |
其中,
步骤 2. 根据式(50), 当满足
3. 算法仿真与验证
为验证控制算法有效性, 本文以图2所示的具有7个支链的冗余驱动绳索并联机器人为控制对象进行算法仿真, 机器人运动学参数与惯性参数如表1与表2, 各部件的惯性张量在其质心处的固连坐标系下测量.
为检验本文提出的预设性能有限时间控制算法的有效性, 将分别进行以下仿真: 1)本文算法 (Prescribed performance sliding mode control, PPSMC); 2)基于时延估计的连续非奇异快速终端滑模控制 (Time delay estimator based nonsingular fast terminal sliding mode control, TDENFTSMC)[14]; 3)基于自适应超螺旋[37]与UDE的非奇异快速终端滑模控制 (Adaptive super-twisting combined UDE based sliding mode control, ASTUDESMC); 4)基于UDE的滑模控制(UDE based sliding mode control, UDESMC)[38]. 在仿真中设置扰动
| (51) |
其中,
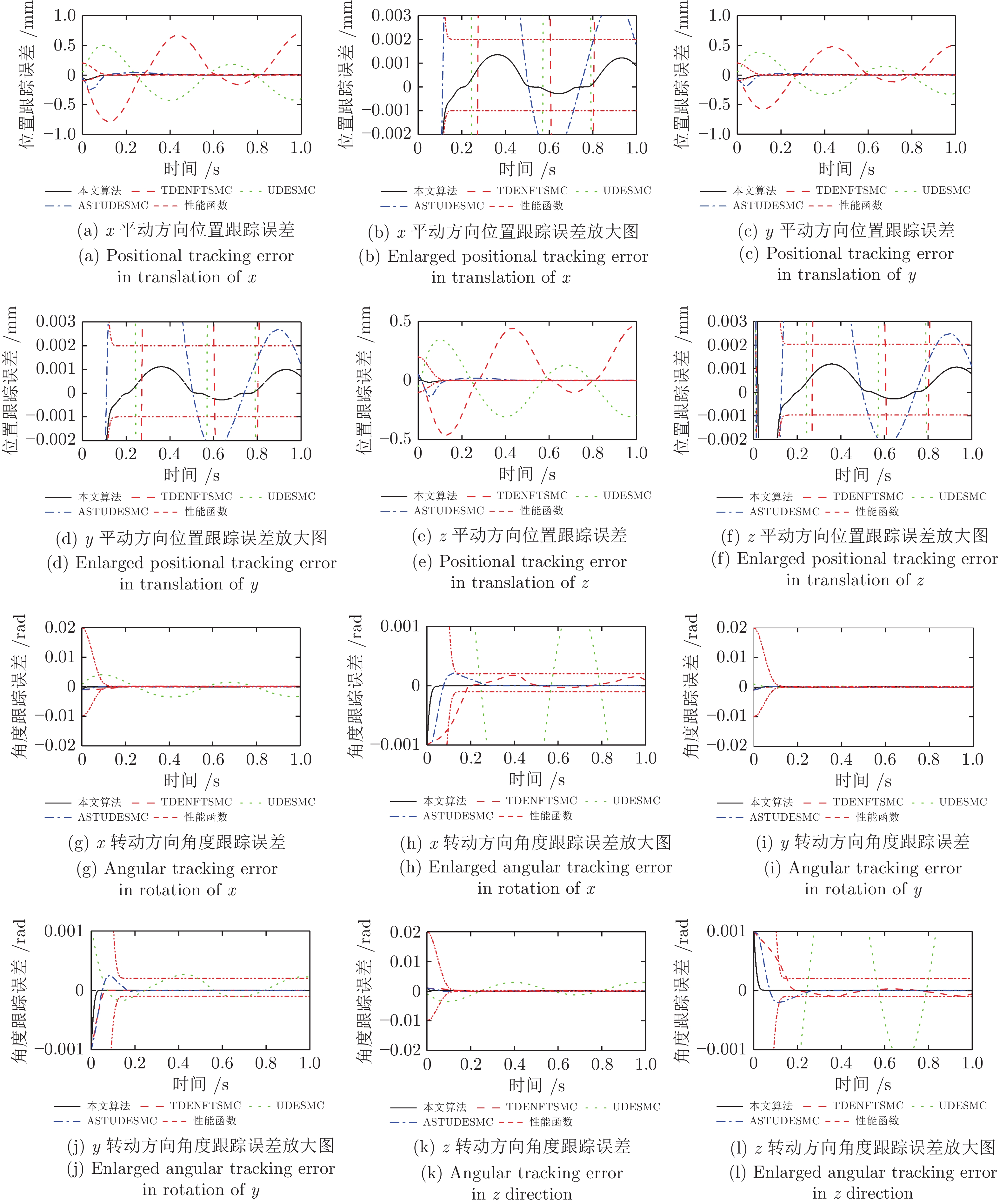
图3所示为位置跟踪误差及其放大图. 由于本文将给定时间Te设为0.2 s, 因此, 0 s至0.2 s为瞬态阶段, 0.2 s至0.5 s为稳态阶段. 对于三个平动方向, 文中预设性能函数的初始值分别为−0.1 mm与0.2 mm, 稳态值为0.001 mm与0.002 mm. 可以看出, 采用TDENFTSMC与UDESMC时, 平动方向位置跟踪误差在整个运行阶段均处于较大波动状态, 波动幅度均达到或接近1 mm, 远超出预设性能函数边界. 因此, 虽然UDE与TDE选取了较小的时间常数, 但对于快时变大扰动, 仅采用扰动观测器仍然难于取得良好的跟踪性能. 当采用ASTUDESMC时, 平动方向位置跟踪误差出现了显著减低, 瞬态阶段幅值在0.25 mm左右, 稳态阶段幅值约为0.004 mm. 虽然也超出了预设性能函数边界, 但与TDENFTSMC与UDESMC相比瞬态与稳态误差分别降低了50%与99%左右, 这是由于ASTUDESMC采用自适应超螺旋算法(Adaptive super-twisting algorithm, AST)对扰动观测误差进行补偿. 同时, 当采用本文算法时, 在整个运行阶段平动方向位置跟踪误差均在预设性能函数边界内. 对于转动方向, 预设性能函数的初始值分别为−0.001 rad与0.002 rad, 稳态值为0.0001 rad与0.0002 rad. 采用UDESMC时, 三个转动方向的稳态与瞬态误差均超出性能函数边界; TDENFTSMC算法在x与z转动方向的瞬态阶段超出了性能函数边界; ASTUDESMC在z转动方向的瞬态阶段超出边界, 其他时刻均在边界内; 采用本文算法时, 角位置跟踪误差均在性能函数边界线以内. 可以看出, 采用本文提出的非对称给定时间预设性能控制时, 位置跟踪误差在瞬态与稳态阶段均可在给定时间实现预设的位置跟踪精度.
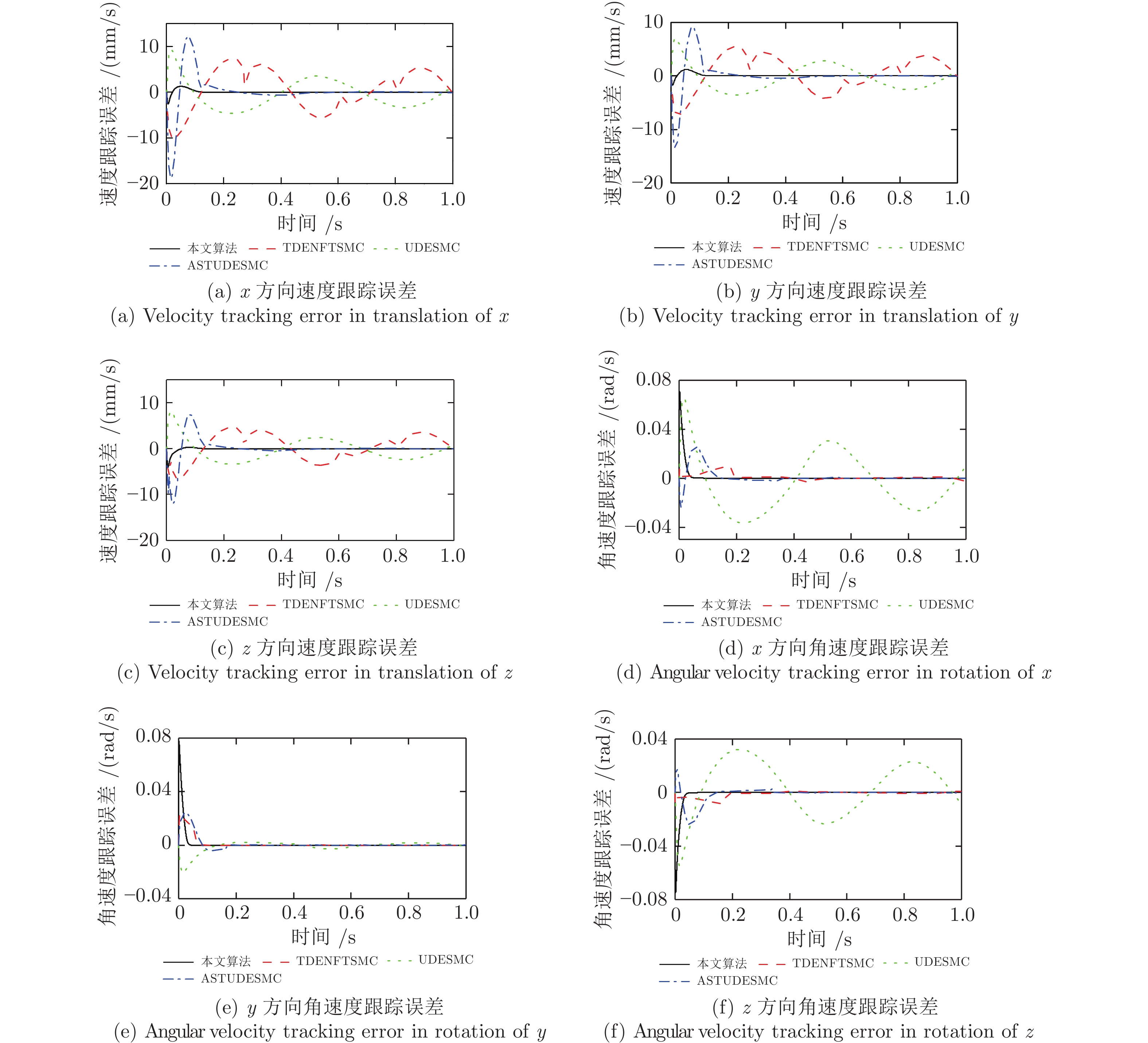
图4所示为速度跟踪误差. 在平动方向上, 采用TDENFTSMC与UDESMC算法时, 平动方向的速度跟踪误差在整个运行阶段均处于大幅度波动状态, 三个平动方向的最大瞬态幅值均在7.4 mm/s与7 mm/s以上, 对应的最大稳态幅值在5.5 mm/s与3.6 mm/s以上; 当采用ASTUDESMC算法时, 三个平动方向的最大瞬态速度跟踪误差分别达到了18.7 mm/s、13.6 mm/s与12 mm/s, 稳态阶段的最大速度误差均小于0.42 mm/s, 且在0.6 s以后对应值小于0.08 mm/s, 这是由于该算法在扰动观测器基础上采用了增益较大的AST算法, 在初始阶段位置跟踪误差较大使得速度波动剧烈, 同时由于采用AST对扰动观测误差进行自适应补偿, 稳态误差与仅使用观测器进行扰动估计的TDENFTSMC与UDESMC相比显著降低; 当采用本文算法时, 三个平动方向的最大瞬态速度跟踪误差与稳态跟踪误差均小于4 mm/s与0.02 mm/s, 远小于其他三种算法. 同时, 在转动方向上, 采用本文控制算法时三个方向的瞬态误差最大, 但稳态跟踪误差最小, 对应值均小于0.00002 rad/s. 这是由于本文在进行仿真时未在转动方向施加运动, 使得采用4种控制器时转动方向上的速度跟踪误差均较小, 同时由于本文采用针对输出约束的预设性能控制, 在保证位置跟踪精度的同时, 由于动力学模型的强耦合性, 在未施加运动的转动方向瞬态速度跟踪误差较大, 而瞬态误差可保证在较小范围.
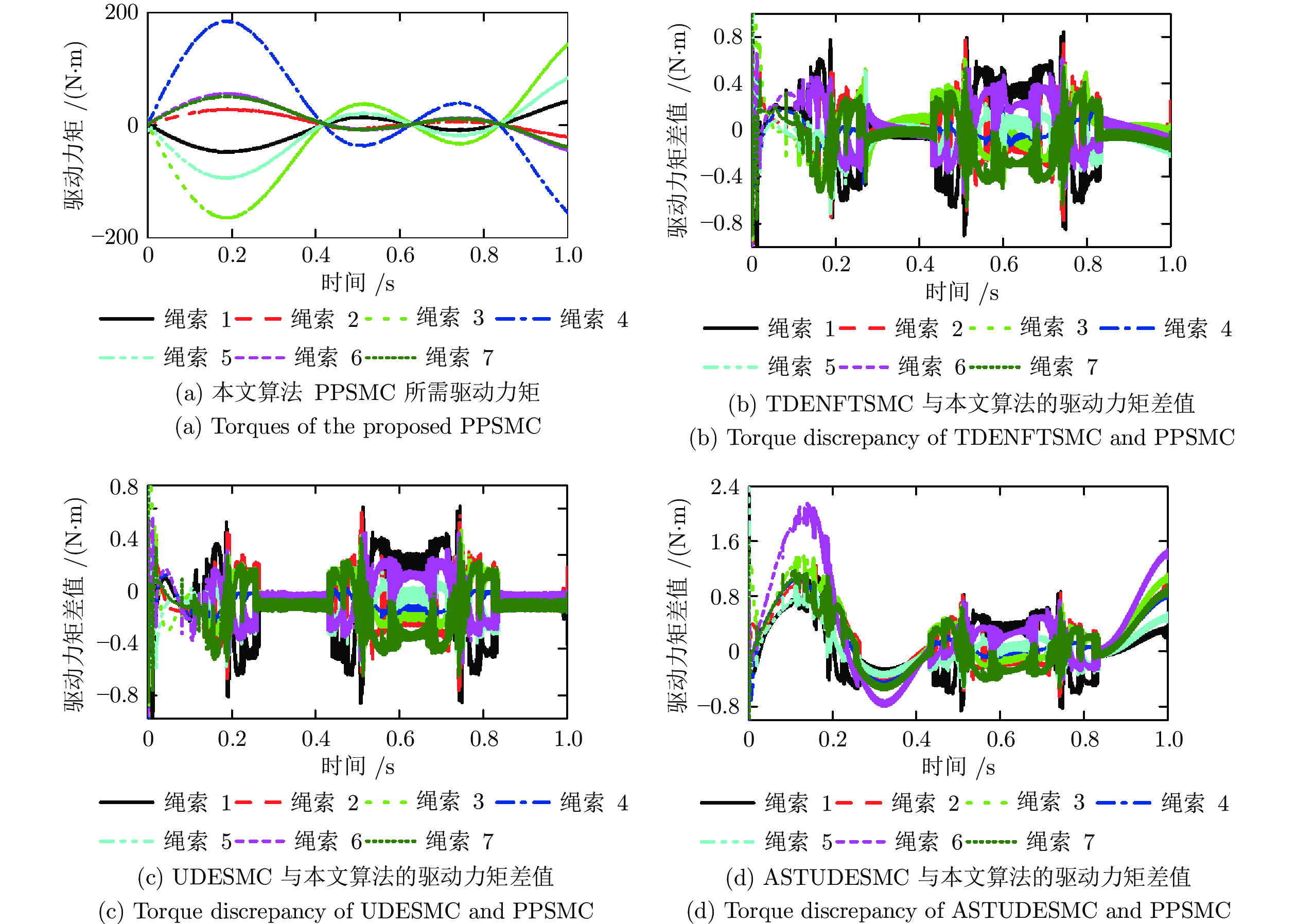
图5所示为采用本文算法时的驱动力矩及其与其他控制算法的驱动力矩差值对比. 可以看出, 采用本文算法时驱动力矩总体较平滑, 驱动绳索3与4的最大驱动力矩值约为200 N·m, 其他各绳索的最大驱动力矩均小于100 N·m, 在实际使用中可以通过增加绳索数目以减小各绳索的最大驱动力矩或引入减速器以提高电机输出力矩进而满足使用要求. 与其他三种控制算法相比, 在初始时刻, 驱动力矩的差值约为 ± 1.5 N·m, 约为此时驱动力矩的 ± 10%, 这是由于采用不同控制算法时各关节驱动力矩分配不同及时间延迟造成的, 并未出现显著的力矩变化. 与TDENFTSMC与UDESMC相比, 在瞬态阶段的最大驱动力矩差值约为 ± 0.8 N·m, 约为此时对应驱动力矩 ± 1.6%; 在稳态阶段, 对应的最大驱动力矩差值也基本处于该水平. 同时, 采用本文算法时瞬态阶段及0.8 s至1 s之间各绳索的驱动力矩值均小于ASTUDESMC算法的对应值, 绳索6的驱动力矩差的幅值约为1.6 N·m, 其他各绳索约为0.7 N·m, 这是由于为实现高精度的跟踪性能, ASTUDESMC算法中AST更新率增益较大产生的, 其他时刻的驱动力矩差的幅值约为0.8 N·m, 与此时驱动力矩相比, 波动幅度较小. 可以看出, 采用本文算法时, 在保证较高的位置跟踪精度时, 驱动力矩并未显著增加, 且与ASTUDESMC相比, 驱动力矩反而减小.
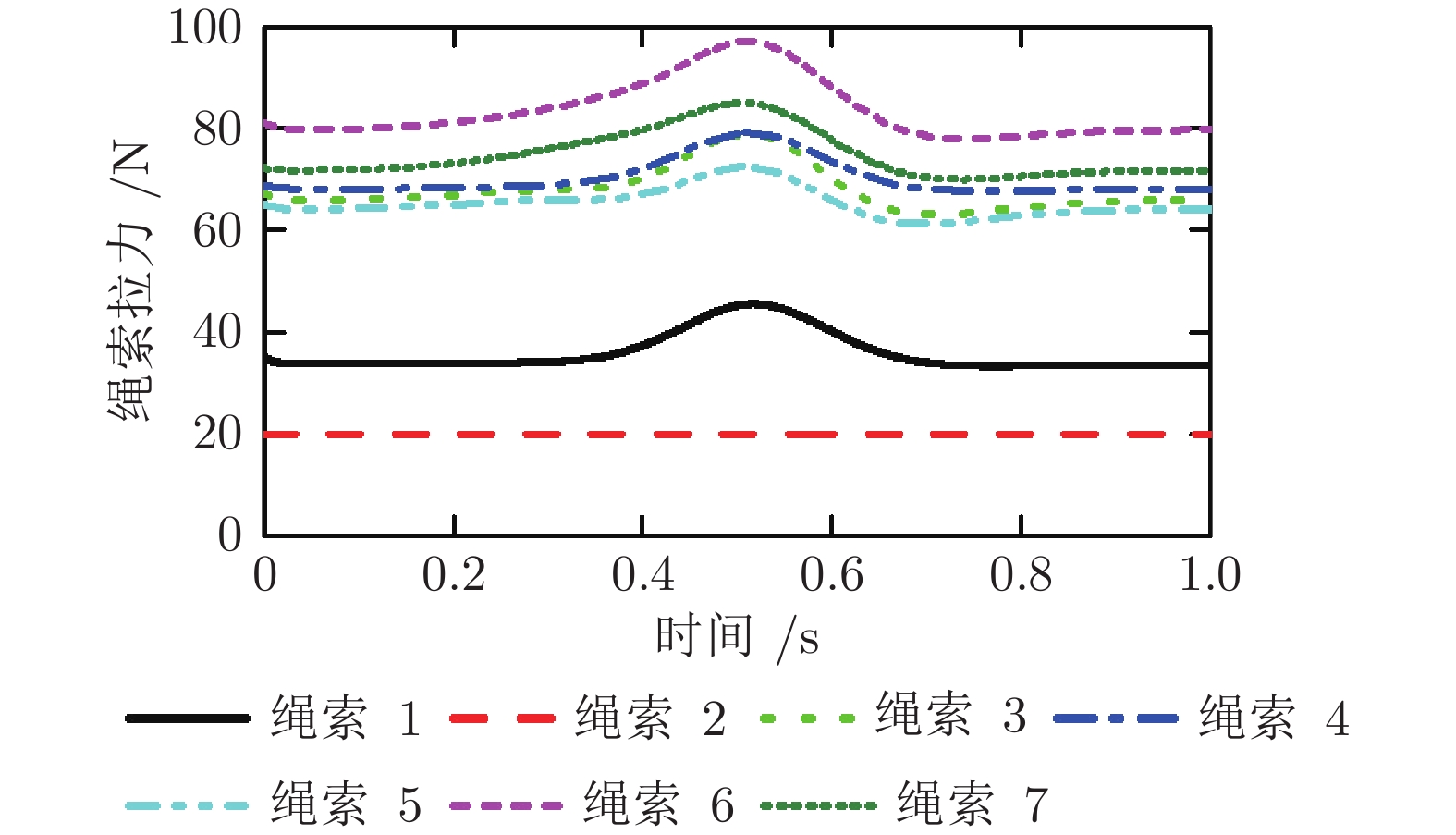
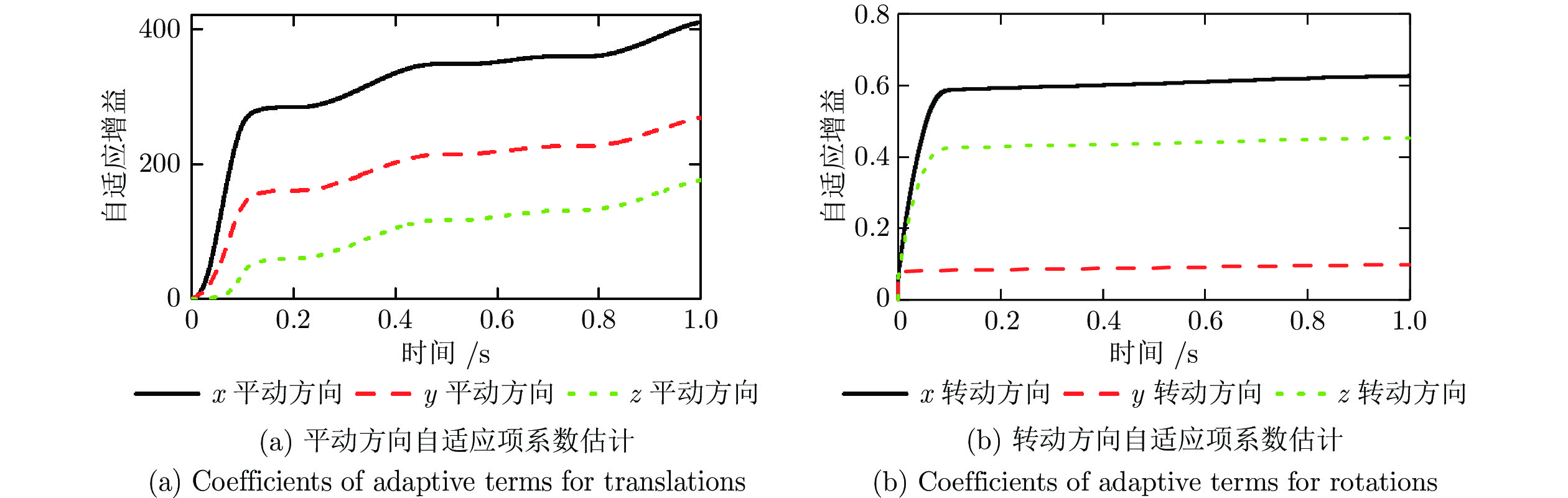
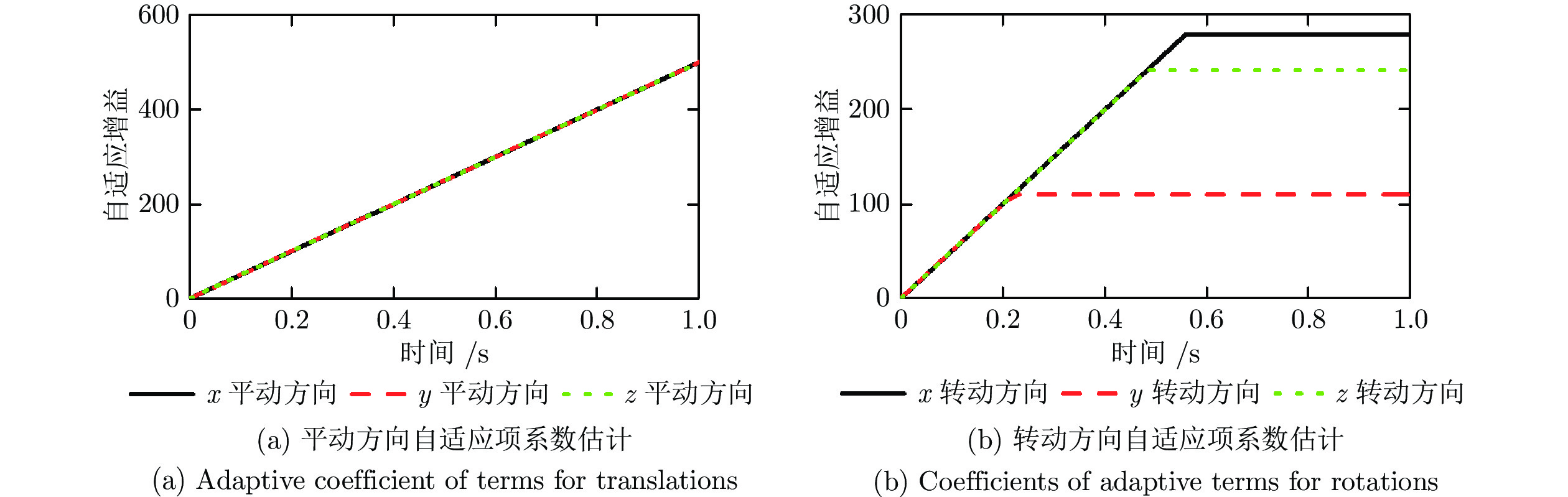
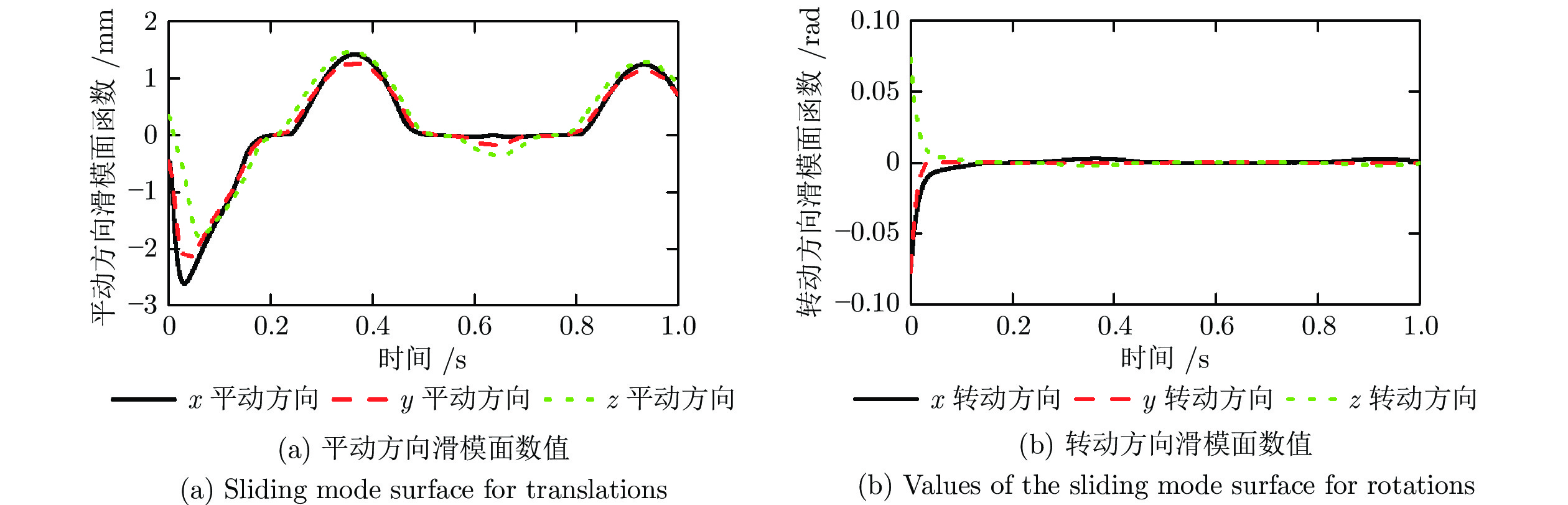
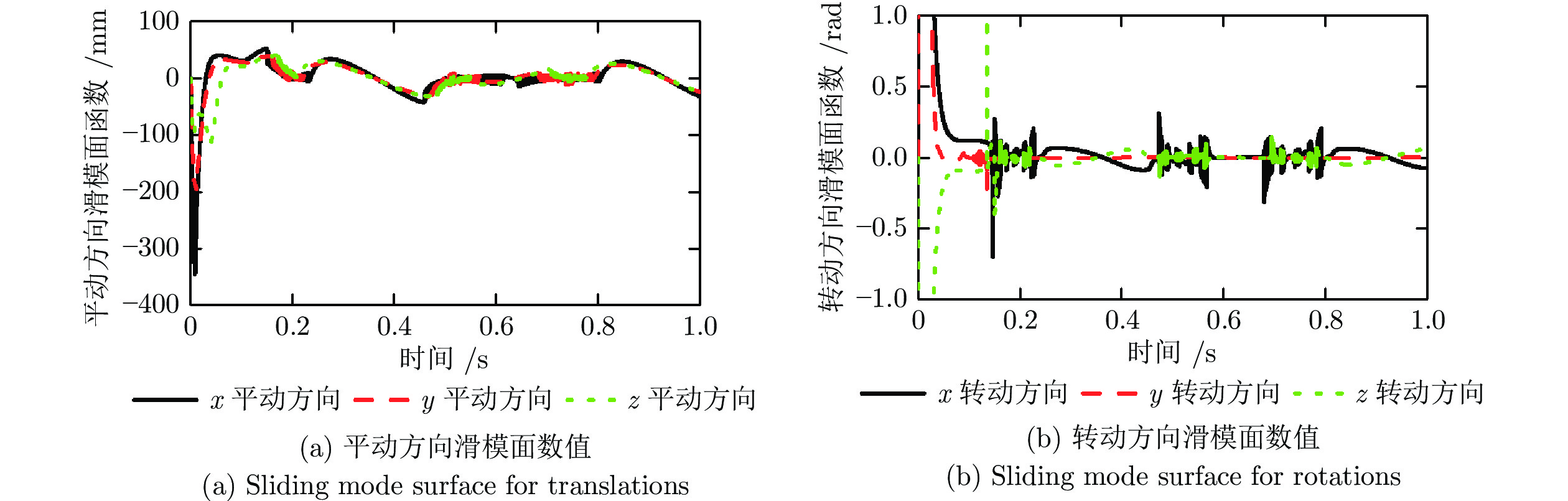
图6所示为采用本文算法时各绳索拉力, 经过优化, 各绳索拉力连续, 且均大于20 N, 即绳索处于拉伸状态, 符合预期要求. 图7与图8分别为采用本文算法与ASTUDESMC时自适应项系数估计值. 采用本文算法时, 由于初始误差较大使得各方向的自适应项系数在初始0.1 s内急剧增加, 之后转动方向上增益基本保持稳定, 而平动方向处于缓慢上升趋势; 而当采用ASTUDESMC时, 平动方向的增益始终处于增大状态, 在终点时刻达到了500, 转动方向的增益在0.1 s后基本保持不变, 均小于0.7, 这是由于转动方向未施加运动, 模型不确定部分较小, 而平动方向施加运动使得模型不确定部分较大, 对于快时变大扰动, 虽然在算法仿真时选取的时间常数较小, 但扰动估计误差依然较大, 使得平动方向增益始终处于增加状态. 图9与图10为采用本文算法时分别基于跟踪误差e与z时各方向的滑模面数值. 可以看出, 由于两种误差尺度的不同, 虽然跟踪误差e可以保证在预设性能函数边界内, 且基于e计算的等效滑模面数值较小, 但基于z计算的滑模面数值在整个运行过程中处于大幅度波动状态, 平动与转动方向瞬态幅值达到了330 mm与12 rad, 稳态阶段的波动幅值达到42 mm与0.3 rad, 因此, 这也解释了采用本文算法时图7所示的变化特点. 提高式(42)中
因此, 从上述位置跟踪误差与力矩的对比研究以及采用本文算法时的绳索拉力及自适应项系数的仿真结果可以看出, 本文提出的控制算法可以实现冗余驱动绳索并联机器人预设性能高精度轨迹跟踪控制.
4. 结论
本文提出了一种考虑输出约束与扰动的冗余驱动绳索并联机器人预设性能有限时间控制算法. 为对机器人的输出进行约束, 设计给定时间衰减函数与非对称变换函数, 并将考虑预设性能的跟踪误差转换为无约束变量; 在此基础上, 设计精度驱动并在连接点处具有三阶连续性能的非奇异快速终端滑模面进行控制算法设计; 为避免滑模控制的抖振问题, 在预设性能控制中采用UDE方法对扰动项进行估计, 同时基于自适应控制对扰动估计误差进行补偿, 并从理论上证明了本文算法具有有限时间收敛特性. 最后以7自由度冗余驱动绳索并联机器人为对象进行仿真研究. 结果表明, 与TDENFTSMC、ASTUDESMC及UDESMC相比, 本文算法得到的位姿跟踪误差始终处于约束边界以内, 速度与角速度跟踪误差收敛速度快, 且驱动力矩并未显著增加, 同时绳索拉力始终不小于设定的20 N, 进而实现了冗余驱动绳索并联机器人的预设性能有限时间控制. 后续将开展具有固定时间收敛特性的扰动观测器及预设性能函数的研究, 进一步减小跟踪误差收敛时间, 同时将搭建实验平台对本文算法进行实验验证.
- GB/T 7714-2025与GB/T 7714-2015相比,变更了哪些,对期刊参考文献格式有什么影响?
- 别被这个老掉牙的报纸理论版投稿邮箱误导了!最新核实91个报纸理论版投稿邮箱通道,一次集齐
- 喜报!《中国博物馆》入选CSSCI扩展版来源期刊(最新CSSCI南大核心期刊目录2025-2026版)!新入选!
- 2025年中科院分区表已公布!Scientific Reports降至三区
- 国内核心期刊分级情况概览及说明!本篇适用人群:需要发南核、北核、CSCD、科核、AMI、SCD、RCCSE期刊的学者
- CSSCI官方早就公布了最新南核目录,有心的人已经拿到并且投入使用!附南核目录新增期刊!
- 北大核心期刊目录换届,我们应该熟知的10个知识点。
- 注意,最新期刊论文格式标准已发布,论文写作规则发生重大变化!文字版GB/T 7713.2—2022 学术论文编写规则
- 盘点那些评职称超管用的资源,1,3和5已经“绝种”了
- 职称话题| 为什么党校更认可省市级党报?是否有什么说据?还有哪些机构认可党报?

 0373-5939925
0373-5939925 2851259250@qq.com
2851259250@qq.com