基于改进动态系统稳定估计器的机器人技能学习方法
近年来, 机器人产业高速发展, 整体规模持续增长, 在制造业和服务业等众多领域都有广泛应用. 随着工业产品迭代速度日益增长, 个性化需要与日俱增, 传统依靠手工编程完成特定任务的方法难以适应新的需求. 因此, 迫切需要开发简单实用, 且可以灵活适用于多种任务的机器人技能学习方法.
机器人示教学习(Learning from demonstration, LfD)的灵感最初来源于人类的模仿学习, 近几年获得学术界和工业界的广泛关注[1–4]. 机器人通过观察用户演示来学习新技能, 同时将新技能泛化到不同场景下的相似任务中去, 一般包含演示、学习、复现三个阶段. 演示阶段需要解决的问题是如何向机器人进行技能演示, 常用的方法有视觉示教、动觉示教、遥操作示教和双臂示教. 学习阶段是对技能进行建模, 抽象的技能符号由示教数据具体表示, 然后利用示教数据训练模型参数. 复现阶段的性能主要体现在稳定性、复现精度、泛化能力和抗干扰性能4个方面.
动态系统(Dynamical system, DS)是对机器人技能进行建模的常用方法[5], 该方法将规划和执行集成到一起, 并将所有可能的解决方案嵌入到模型中以实现目标[6]. 在非线性DS基础上发展起来的动态运动原语只要进行一次演示就可以对运动进行建模[7], 动态运动原语描述的运动模型由非线性DS和线性DS组成, 其中非线性部分保证了轨迹复现的相似度, 线性部分则确保了模型全局稳定性, 两者的切换依靠相位变量平稳进行. 尽管动态运动原语提供了一种有效而精确的方法来对复杂的动态进行编码, 但是单变量编码丢失了各自由度之间的相关信息, 而且该方法本质上仍依赖于时间, 在面对时间扰动时需要用启发式方法重置相位变量[8].
为弥补动态运动原语的缺陷, 文献[9]提出了动态系统的稳定估计器(Stable estimator of dynamical systems, SEDS). 它首先利用高斯混合模型(Gaussian mixture models, GMM)和高斯混合回归(Gaussian mixture regression, GMR)的概率学习方法对轨迹进行初步拟合. 概率学习方法是轨迹编码中的常用方法, 它可以保留演示的固有可变性[10], 但是无法确保训练得到的动态系统具有全局稳定性. 因此SEDS在后续优化中加入了稳定性约束, 确保机器人在不受扰动的情况下能够到达目标点. 然而, 过于严格的稳定性约束可能会在学习过程中限制模型的精度. 针对SEDS方法中稳定性和精度难以平衡的问题, 文献[11]利用微分同胚变换改进了SEDS, 称作
SEDS中另一个值得注意的问题是混合高斯分量个数的选取, 但是对于该问题的相关研究较少. 过多或者过少的分量个数选取都会导致模型无法有效提取演示的动力学特征, 因此该问题具有一定的研究价值. 通常用于确定有限混合模型的最佳分量的方法是贝叶斯信息准则[14], 然而这种模型选择方法存在一些明显的缺陷[15], 常常过高估计模型分量的个数, 导致过拟合. 贝叶斯非参数模型是一种定义在无限维参数空间上的贝叶斯模型, 其利用在适当数量的模型分量密度上产生后验分布来调整模型大小, 因此可以根据数据自适应聚类个数, 其中狄利克雷过程混合模型是最常用的贝叶斯非参数模型之一[16-18]. Figureoa等[19]提出了一种物理一致的贝叶斯非参数混合模型, 该方法可以自动估计最佳的混合分量个数, 并且将相似性测度融入先验信息, 提高了复现和泛化的精度. 但是该方法使用吉布斯采样计算模型的后验概率, 计算复杂度较高.
鉴于SEDS存在的上述缺陷, 本文提出了改进的SEDS (Improved SEDS, i-SEDS). 该方法有效地解决了SEDS中稳定性和精度无法兼顾的问题, 并且可以自动确定合适的分量个数. 仿真以及Franka-panda协作机器人的实验结果验证了本文方法的有效性和优越性. 本文的主要贡献有: 1)使用狄利克雷过程高斯混合模型(Dirichlet process GMM, DPGMM)代替GMM拟合演示, 并利用变分推断(Variational inference, VI)训练模型, 该模型可以根据演示数据自动确定合适的混合分量个数. 仿真分析超参数对DPGMM的影响, 为超参数的选择提供了指导意义; 2)采用参数化的李雅普诺夫函数修改了原SEDS中的稳定性约束条件, 从而提高了学习轨迹的精度, 解决了稳定性和精度难以兼顾的问题.
1. 问题描述
将机器人离散运动公式化为由自治动态系统驱动的控制律. 考虑一个状态变量
| (1) |
式中,
通常, 将基于一组M条演示轨迹的数据
SEDS使用GMM-GMR回归方法从演示中估计初始DS. 首先利用具有
| (2) |
式中,
上述方法有足够的灵活性来建模各种运动, 但是无法确保DS的渐近稳定性, 为此, SEDS给出了在保证系统稳定性下的参数学习方法, 即通过最小化带非线性项约束的目标函数来估计参数
| (3) |
式中,
| (4) |
式中, 对数ln也可换成以其他常数为底的对数, 上式的约束是
定理1. 如果存在径向无界且满足式(5)的Lyapunov函数
| (5) |
SEDS方法可以有效地从演示中估计出具有全局渐近稳定性的DS, 是LfD领域中的常用方法, 但是该方法存在两个问题: 1)用于估计初始DS的GMM-GMR方法需要人工指定混合分量个数
针对问题1), 本文利用贝叶斯非参数模型能根据数据自动确定最佳聚类个数的特性, 采用了DPGMM拟合演示数据, 并推导GMR估计初始DS; 针对问题2), 本文选择参数化QLF (Parametrized QLF, P-QLF)来确保估计DS的稳定性, 即
2. DPGMM-GMR算法
DPGMM-GMR算法由DPGMM的建模过程、利用变分推断进行模型求解和推导GMR估计初始DS三部分组成.
2.1 狄利克雷过程高斯混合模型
狄利克雷过程(Dirichlet process, DP)一般用
| (6) |
折棍过程(Stick breaking process, SBP)通常用于建模和推断DP[23]. 给定两个无限随机变量
| (7) |
式中,
通过SBP, 可以将独立于
为了便于表述, 将全部演示数据表示为
| (8) |
式中,
在狄利克雷过程混合模型的基础上明确定义基分布
| (9) |
| (10) |
式中,
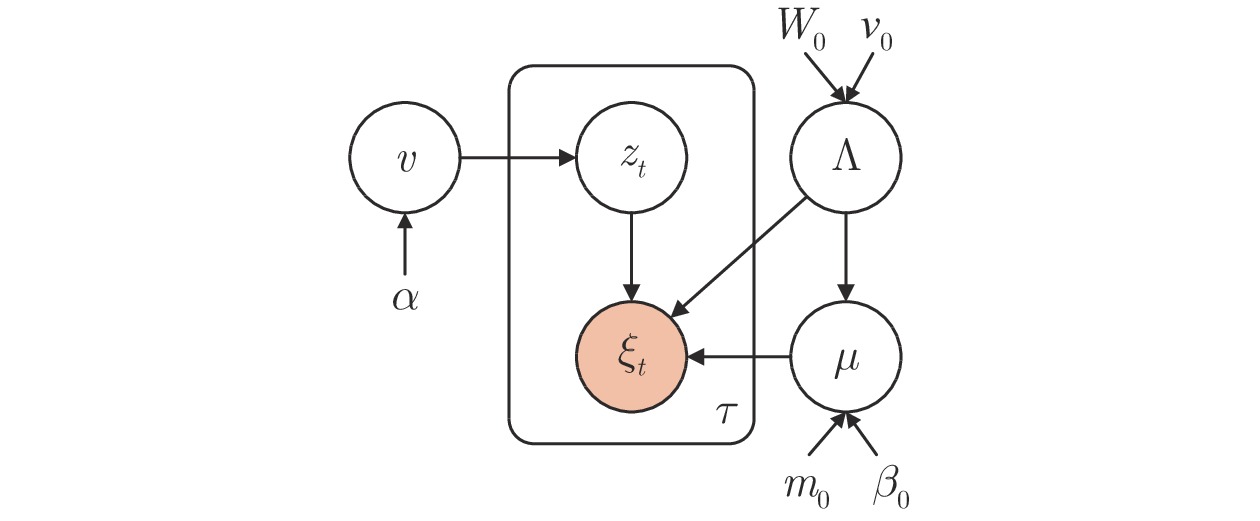
式(9)是给定的共轭先验分布, 式(10)是模型的似然函数. DPGMM的概率结构如图2所示. 然而在无限维的设定下, 实际中模型不易处理. 因此本文采用一种常见的策略, 即基于DP的截断SBP[24]. 预定义最大的混合分量数
2.2 变分推断
第2.1节已为所有随机变量明确定义了共轭先验和模型的似然函数, 本节采用变分贝叶斯方法得出参数可靠的后验分布. 将隐变量和未知参数表示为
| (11) |
其中
| (12) |
| (13) |
同时, 考虑DPGMM的共轭先验配置, 根据共轭的定义, 期望后验
| (14) |
指示变量
| (15) |
式中,
采用变分贝叶斯期望最大化(Expectation maximization, EM)算法. 对该模型参数进行迭代求解. 该算法类似于EM算法, 在E步中, 计算指示变量的期望; 在M步中, 该期望值用于重新计算其他参数的变分分布.
期望通过变分推断得到DPGMM模型参数的后验分布后, 可以得到如下的模型联合概率密度:
| (16) |
式中,
| (17) |
式中,
2.3 GMR估计初始DS
与基于GMM的GMR一样, 先对式(16)的DPGMM中的均值和方差进行划分.
| (18) |
给定输入位置
| (19) |
其中
然后将
| (21) |
DPGMM在拟合演示轨迹时, 自动确定最佳分量个数
| (22) |
式中,
3. 基于P-QLF的稳定DS估计
第2节利用DPGMM-GMR从演示中估计初始动态系统
P-QLF通常用于确保线性时不变(Linear time- invariant, LTI)系统的稳定性, 如命题1所述.
命题1. 形式为
| (23) |
证明. 见文献[19].
命题1易扩展到式(22)表示的线性参数可变系统中, 即
命题2. 式(22)中定义的非线性DS在吸引子
| (24) |
式中,
证明. 如果存在连续且可微的李雅普诺夫函数
| (25) |
由于其二次形式, 可以确保
| (26) |
将
不难发现式(4)的约束条件是式(24)的一种特殊情况, 即当
4. 实验
仿真实验在人类手写数据库(LASA数据集)和Franka-panda机器人上进行, 实验结果验证了本文提出方法的有效性.
4.1 DPGMM-GMR算法性能分析
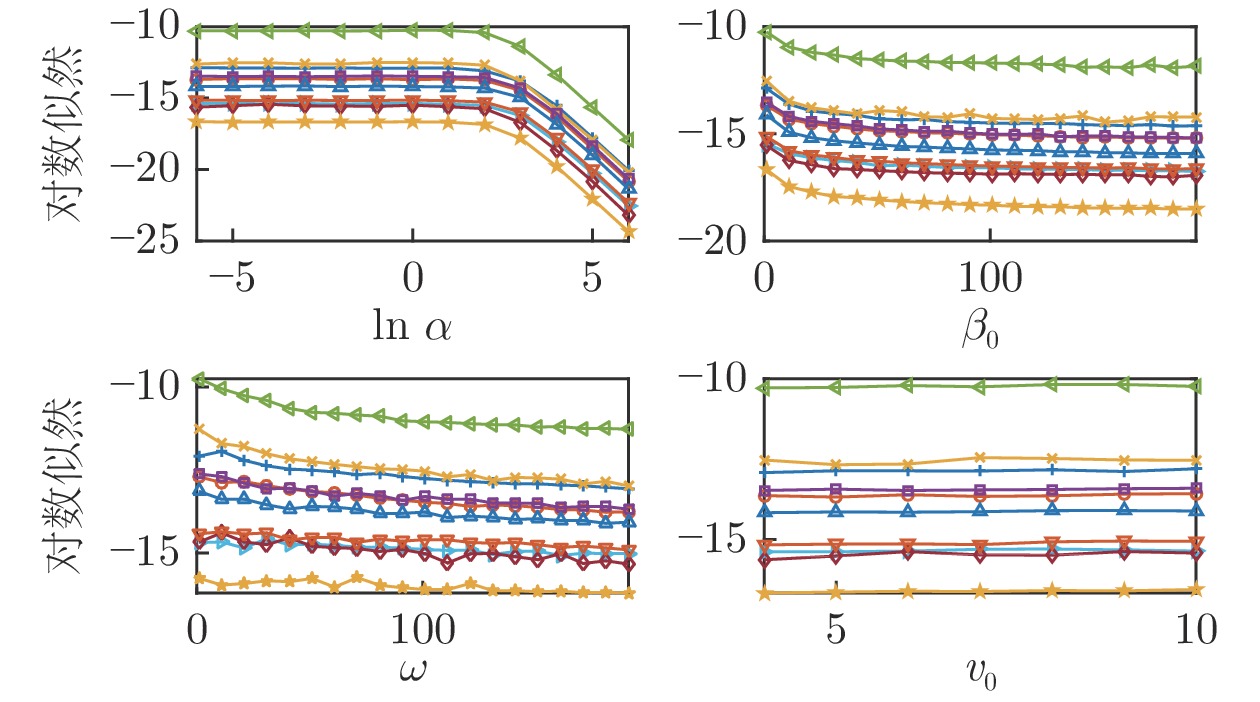
尽管利用DPGMM对演示进行拟合可以自动确定合适的聚类个数, 但该方法引入了更多的超参数
对10组演示训练得到10个DPGMM, 用对数似然值给模型打分, 数值越高则说明模型拟合效果越好. 10个模型的对数似然值相对于各个超参数(固定其他超参数只变化一个超参数)的变化趋势如图3所示. 由图3可以看出: 1)模型对于超参数的变化不敏感, 一般
接着, 在整个LASA数据集上定量评估基于VI的DPGMM-GMR算法拟合初始DS的效果, 超参数均设置为
| (27) |
式中,
4.2 i-SEDS学习方法性能分析
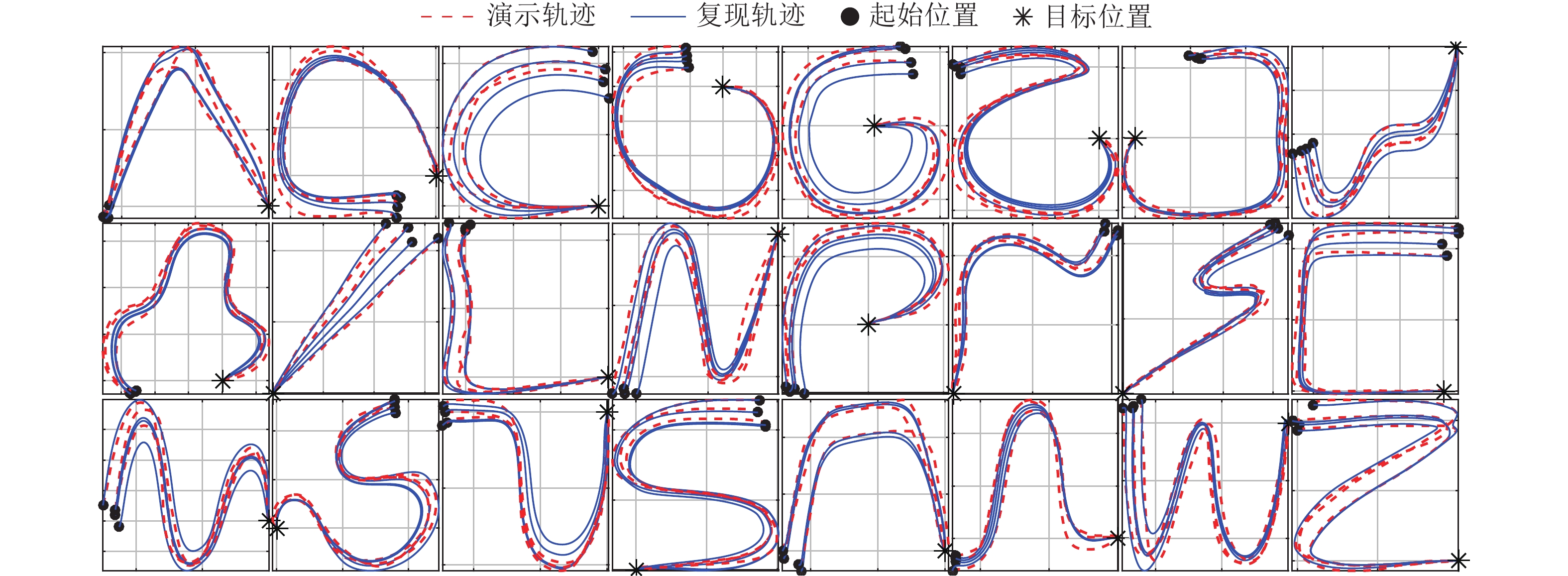
本节i-SEDS的性能分析同样在数据集LASA上进行, 如果算法能够使复现的轨迹紧密(准确)地跟随演示轨迹, 则表明该算法可以令人满意地解决稳定性和精度的难题.
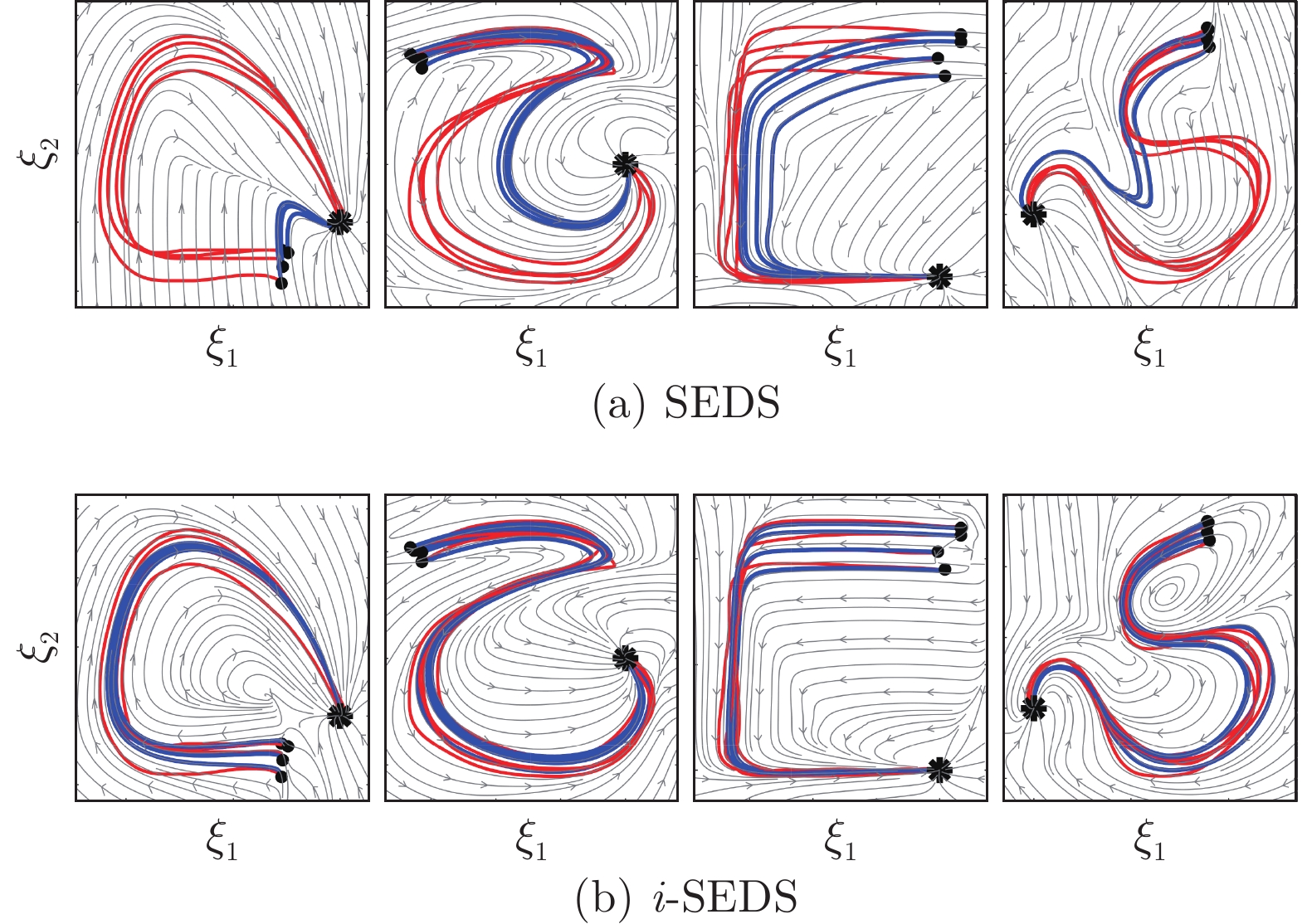
由图4可以看出, 所有复现轨迹紧密跟随了演示轨迹, 仿真结果说明了i-SEDS的有效性. 图5给出了SEDS和i-SEDS在部分不收缩轨迹上的复现结果. 可以看出, SEDS生成的轨迹完全偏离了演示, 这是由于遵循QLF稳定性结果导致的. 图5定性地说明了i-SEDS可以较好地解决SEDS稳定性和精度的难题.
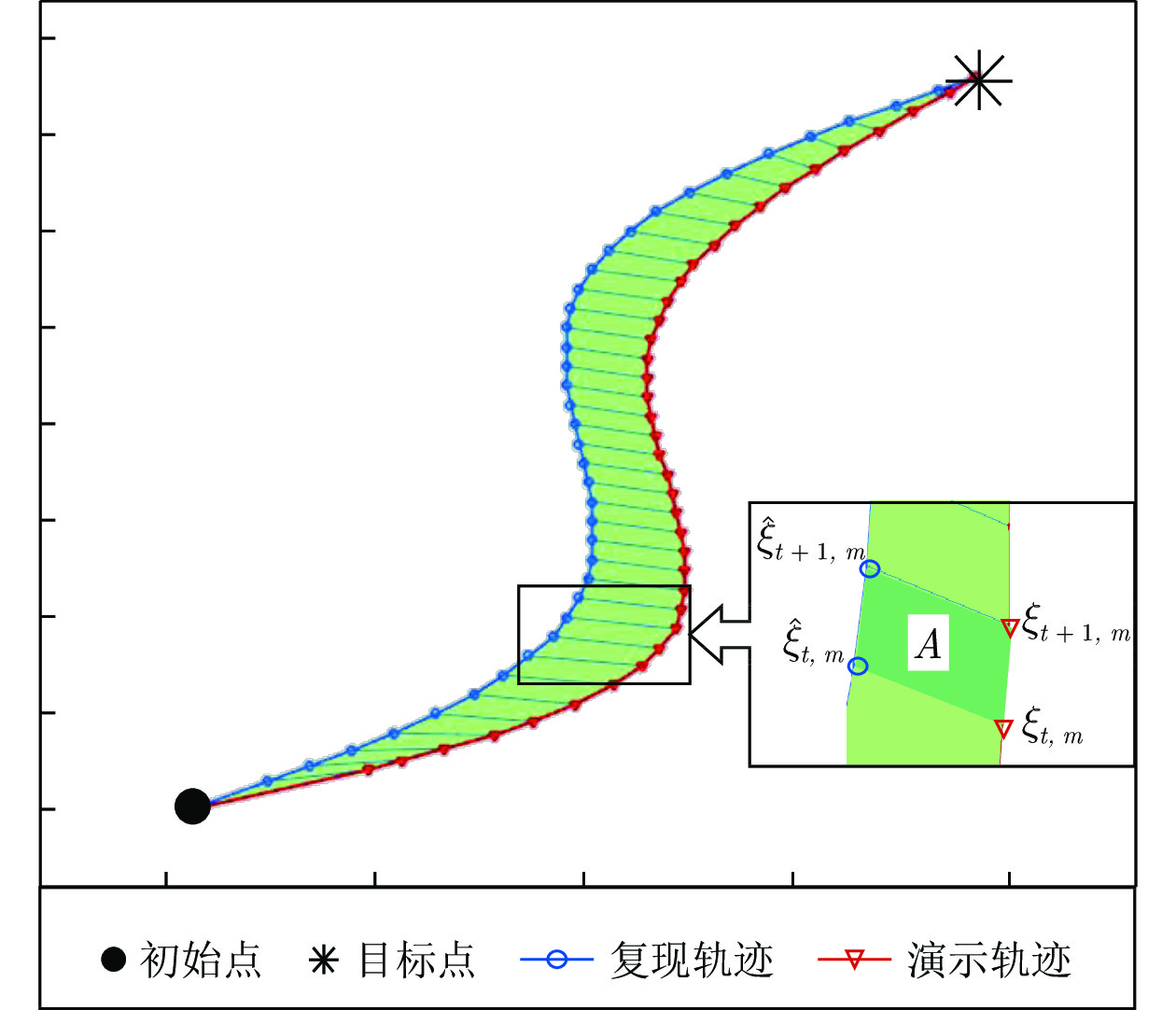
为了定量分析该方法的有效性, 使用文献[28]提出的扫描误差区域(Swept error area, SEA). SEA方法计算了演示轨迹和复现轨迹之间的面积, 计算公式如下:
| (28) |
式中,
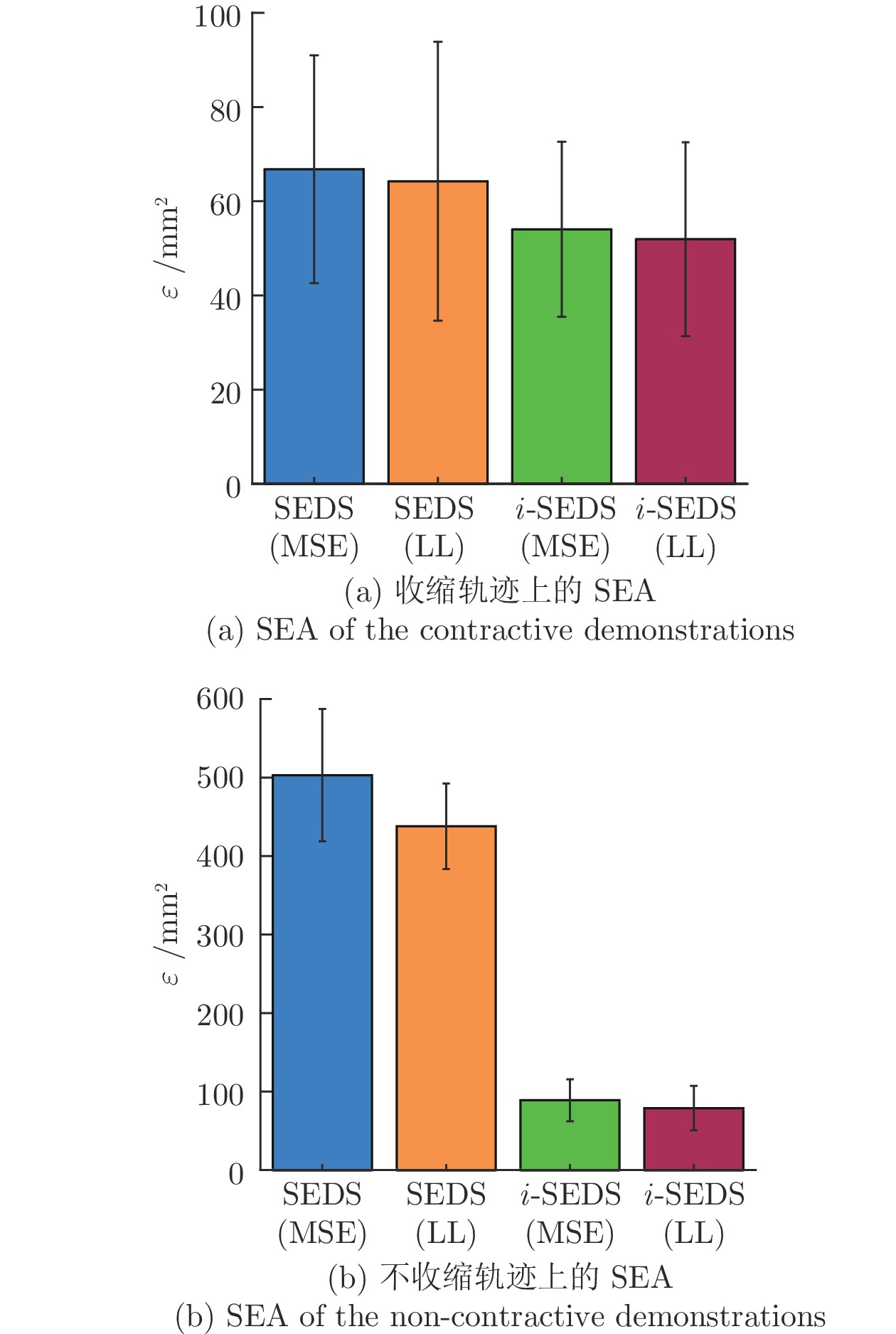
考虑到原始SEDS中2种不同的目标函数MSE和LL, 以及i-SEDS在学习不收缩演示轨迹时具有明显优势. 因此利用SEA方法定量分析i-SEDS (MSE)、i-SEDS (LL)、SEDS (MSE)、SEDS (LL)四种方法分别在收缩和不收缩演示轨迹上的性能. 从LASA数据集中取收缩轨迹和不收缩轨迹各10组, 分别使用上述4种方法学习稳定DS, 计算相应的SEA, 结果如结果如图7所示. 从图7(a)可以看出, 四种方法的SEA在收缩轨迹上差别并不明显, i-SEDS仅略优于SEDS方法. 但在不收缩轨迹组的图7(b)中, i-SEDS方法的复现精度要明显优于SEDS方法. 基于LL的方法精度要略高于MSE, 但MSE的计算速度更快, 因此, 在实际使用中可以根据需求进行选择.
4.3 机器人实验
为了验证本文方法的有效性, 在7自由度的机械臂Franka-panda机器人上进行了实验验证.
机器人实验是在操作空间中学习物块搬运任务, 如图8所示. 这是一个点到点运动的任务, 机械臂需要学会如何从机械臂初始位置到达物块放置位置, 然后拾取物块将其放入目标容器中, 整个过程由拾取物块−放置物块2部分组成, 并利用Kinect摄像头对物体进行跟踪.
1)示教: 首先设置panda机械臂为示教模式, 再由演示人员拖动机械臂完成拾取物块−放置物块2个步骤, 整个示教过程如图8所示. 然后不断调整物块起始位置重复上述示教过程共8次, 同时以10 Hz频率记录机械臂末端位置和速度, 获取8条演示轨迹数据, 记作
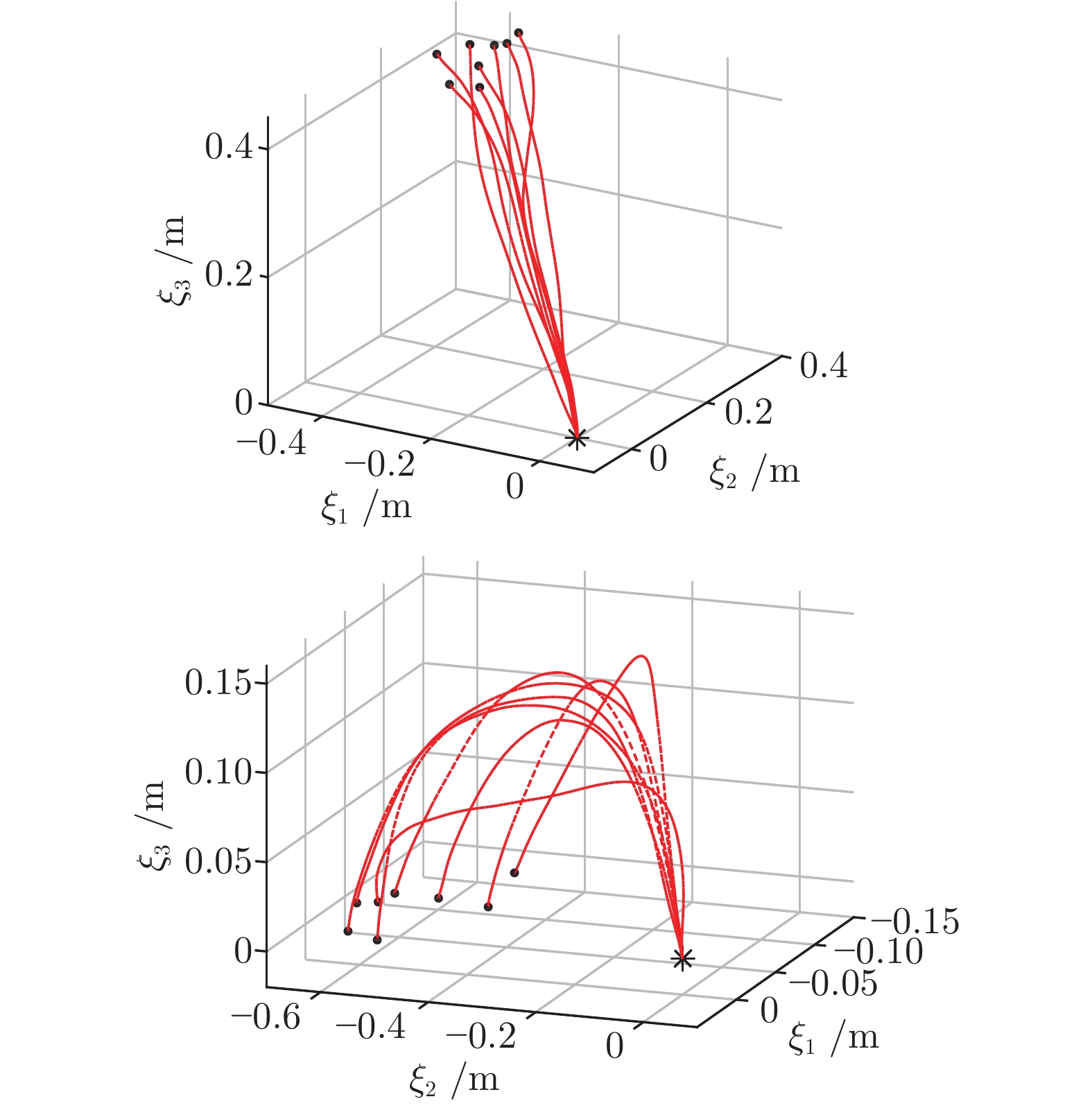
2)学习: 在对演示轨迹建模前, 需要对数据进行一些预处理. a)轨迹平滑: 使用移动均值滤波对采集到的演示数据进行平滑处理. b)任务分割: 为了降低任务的学习成本, 将物品搬运任务分解成拾取物块−放置物块2个子任务. 根据2个子任务切换过程中机械臂末端速度为零这一特点将演示轨迹分成2段, 然后各自进行学习. c)目标位置原点化: 为保证动态系统的参数不会随目标位置的变化而变化, 需要将参考坐标系的原点设在目标位置处. 2个子任务的演示轨迹都转化为以原点为终点的轨迹. 预处理后的演示轨迹如图9所示.
使用
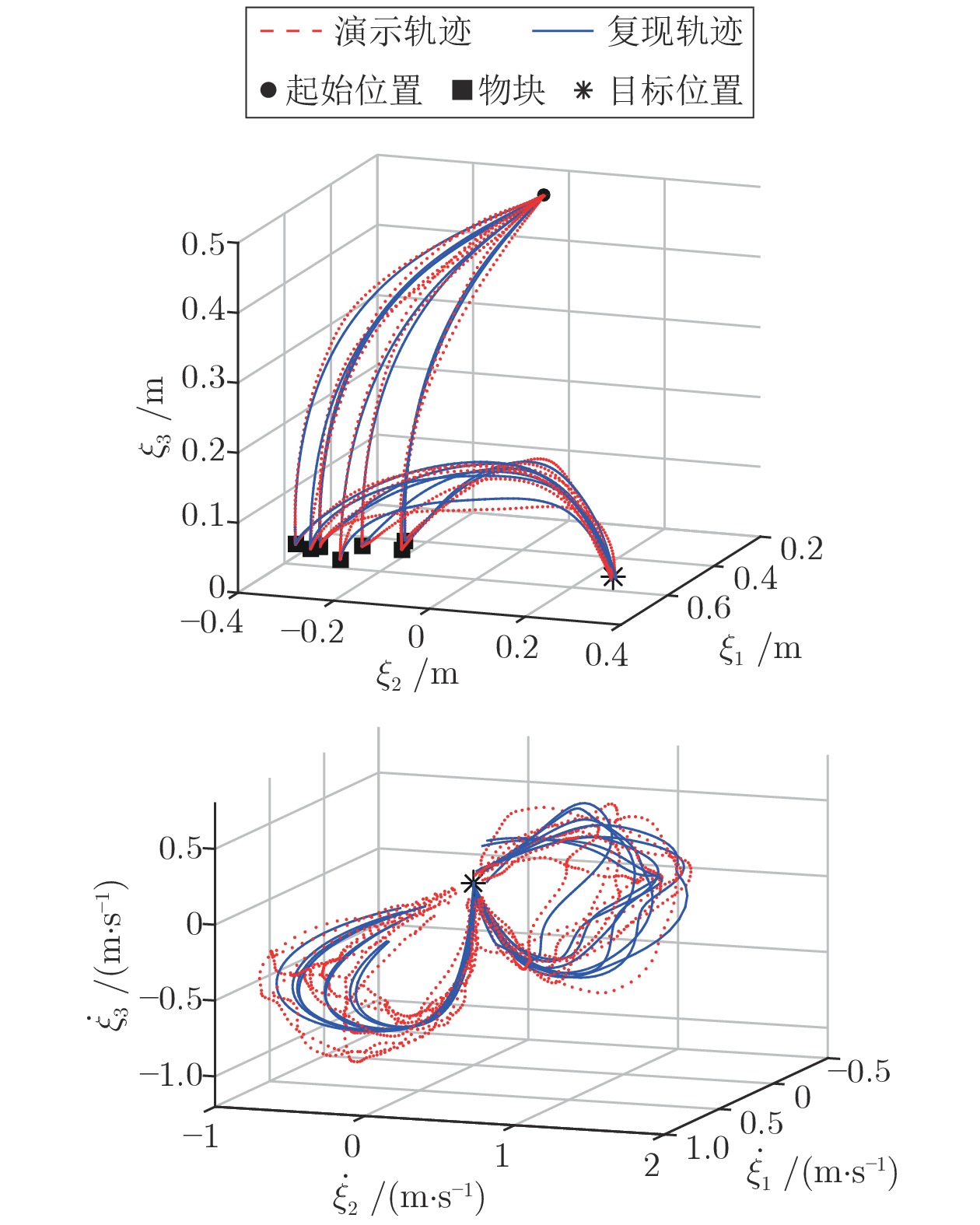
3)复现. 机械臂从初始位置开始, 通过模型不断迭代得到当前位置下的期望速度
a)目标位置的变化. 图11显示了模型对环境变化的鲁棒性, 其中虚线表示原始复现轨迹, 实线表示在
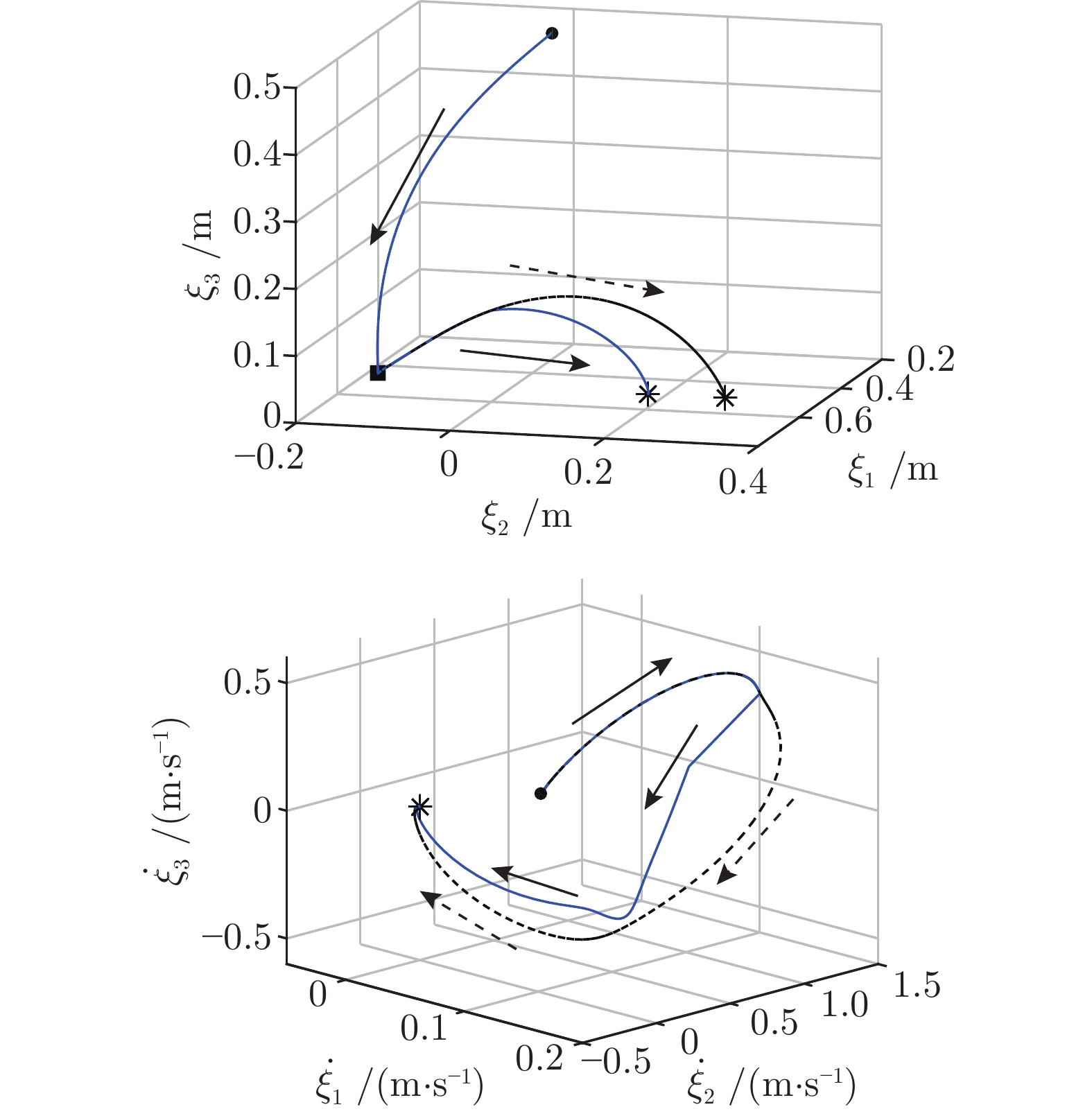
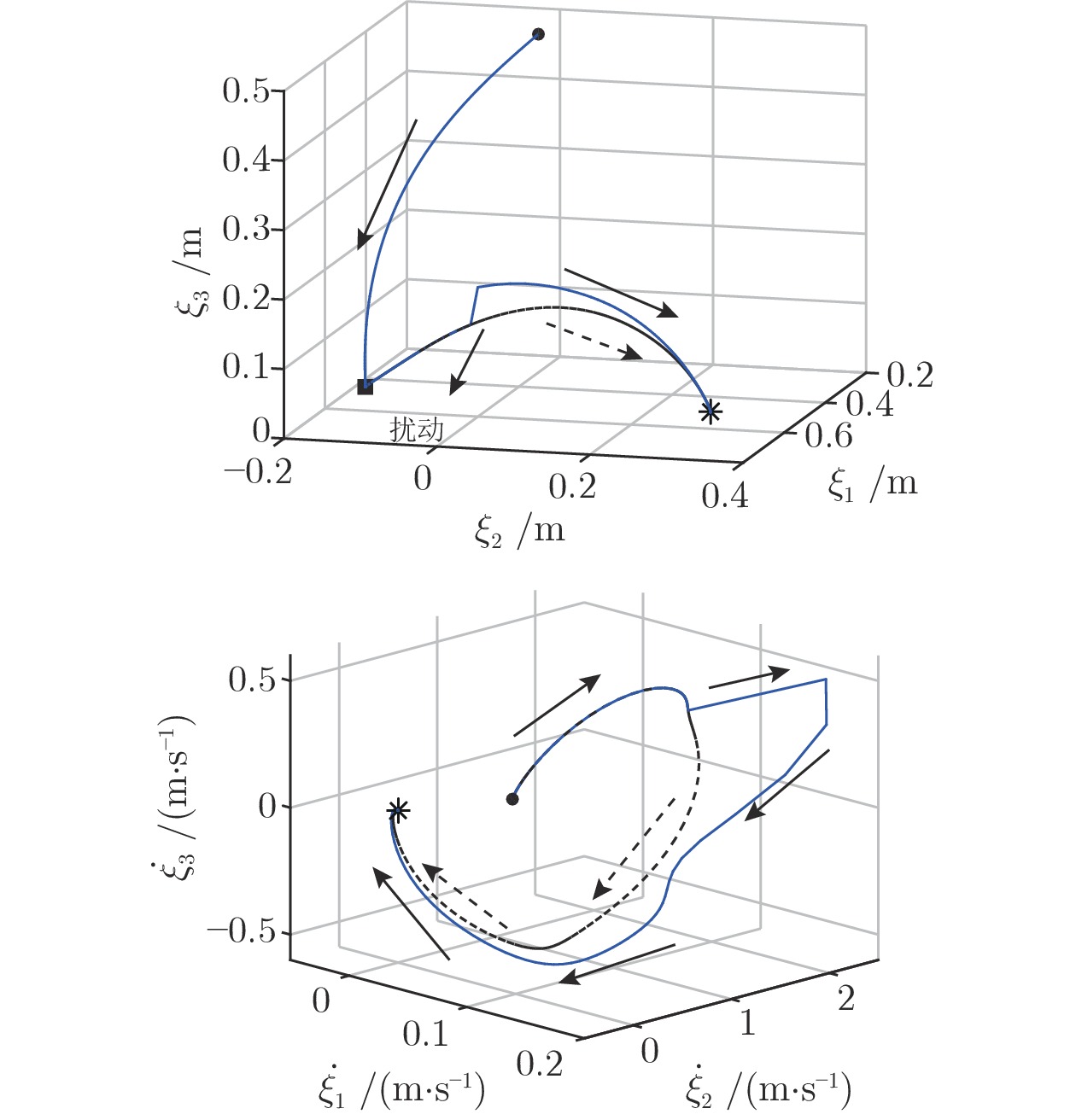
b)抗扰动能力. 图12显示了模型对外界扰动的鲁棒性, 在
上述机器人实验展示了i-SEDS方法在确保稳定性的前提下, 仍具有良好的复现精度以及泛化能力和抗扰动能力.
5. 结束语
本文分析了SEDS方法中存在的缺陷, 并给出了合理的解决方案. 首先利用DPGMM对演示数据进行拟合, 并使用变分推断求解模型参数, 推导GMR拟合初始DS. 解决了基于EM算法的GMM难以确定混合分量个数的难题. 然后利用P-QLF推导新的宽稳定性约束取代原有约束, 最后结合目标函数优化得到能精确复现的稳定DS. 在LASA数据集中验证了DPGMM超参数的性质和其推导的GMR算法的性能, 以及i-SEDS方法在不收缩轨迹上的优越性能. 最后通过Franka-panda协作机器人上的实验, 验证了本文方法在实际场景的有效性. 在未来工作中, 将降低本文方法模型的复杂度.
- 别被这个老掉牙的报纸理论版投稿邮箱误导了!最新核实91个报纸理论版投稿邮箱通道,一次集齐
- 喜报!《中国博物馆》入选CSSCI扩展版来源期刊(最新CSSCI南大核心期刊目录2025-2026版)!新入选!
- 2025年中科院分区表已公布!Scientific Reports降至三区
- 国内核心期刊分级情况概览及说明!本篇适用人群:需要发南核、北核、CSCD、科核、AMI、SCD、RCCSE期刊的学者
- CSSCI官方早就公布了最新南核目录,有心的人已经拿到并且投入使用!附南核目录新增期刊!
- 北大核心期刊目录换届,我们应该熟知的10个知识点。
- 注意,最新期刊论文格式标准已发布,论文写作规则发生重大变化!文字版GB/T 7713.2—2022 学术论文编写规则
- 盘点那些评职称超管用的资源,1,3和5已经“绝种”了
- 职称话题| 为什么党校更认可省市级党报?是否有什么说据?还有哪些机构认可党报?
- 《农业经济》论文投稿解析,难度指数四颗星,附好发选题!

 0373-5939925
0373-5939925 2851259250@qq.com
2851259250@qq.com