基于模拟退火算法的真实多孔电极中热-质传递的研究
电场作用下电极中电化学反应-热质传递现象是典型的多尺度问题[1-3],如图1所示。微观尺度(电子-离子迁移、晶格稳定性)、介观尺度(界面热/动力学、热-质传递、电流电压分布)和宏观尺度(散热性能、充放电管理)的传递和反应特性,直接决定系统中的浓度分布和反应速率,最终影响储能转化效率。而系统中发生传递和反应过程的场所主要在多孔电极中,且多孔电极的不规则表面引起的限域效应显著影响着其内的传质和传热过程,所以深入研究介观尺度下多孔电极中的热-质传递现象及其耦合机制,对高性能电化学储能器件的设计有重要意义[3]。但是,与平板电极不同,对多孔电极中热-质传递现象的研究存在两个关键问题:一方面,多孔电极丰富的孔道体系、多样化的表面形态和分布复杂的催化活性位点,难以用传统数学工具去准确描述其结构[4-6];另一方面,多孔电极中发生的过程涉及在受限空间中的离子迁移、热量产生和传递、双电层形成、电子传递的耦合,极大地影响了离子和热量在孔道中的传递过程,并难以直接用实验进行原位表征[7-8]。因此,多孔电极中的热-质传递的研究一直以来都难以获得突破性进展。
图1
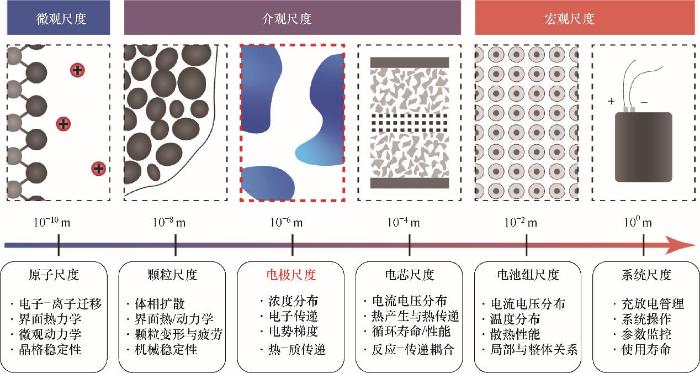
图1 储能和转换过程中的电极尺度问题及与其他尺度问题的联系
Fig.1 The electrode scale issues in energy storage and conversion processes and their relation to other scale issues
目前,研究者们可以采用密度泛函理论 (DFT)[9-10]和分子动力学(MD)模拟[11-12]等方法研究纳米级多孔结构中的演化过程和充电机理。例如纳米多孔电极与离子液体的结合是提高超级电容器能量密度的重要手段。然而,这总是伴随着功率密度的降低,特别是考虑到高黏度和大空间位阻的离子液体。Gan等[11]利用MD模拟发现在阈电位作用下,具有疏离子孔的电极内的离子呈现出一种新的充电机制,即离子吸附。进一步得到了充电时间/电容与电压/耐离子性能之间的定量关系,以评价协同提高超级电容器能量密度和功率密度的临界条件。虽然DFT和MD模拟可以考虑微观粒子间的作用力,但是受限于计算能力的瓶颈,只能模拟离子浓度和温度在含周期性边界条件的高度有序的纳米级多孔结构(如分子筛和金属有机框架)中纳秒级的演化过程,并不能全面描述真实多孔电极中,尤其是常见的无定形碳电极中的离子和热量的传递过程[9]。连续介质模型通过偏微分方程组描述离子浓度和电势的状态演化及其本构关系,可以建立纳米级及以上空间尺度的复杂的多物理场耦合关系[13]。例如,Tao等[14]采用基于Poisson-Nernst-Planck(PNP)方程和Navier-Stokes方程的组合方法,通过控制氧化石墨烯膜的偏置角度,研究了不同层间距分布的氧化石墨烯膜中离子的输运现象。d′Entremont等[15]从第一性原理推导出控制能量方程,并与修正PNP模型相结合,从而得到由于离子扩散、空间效应和混合熵的变化而产生的不可逆焦耳热和可逆热产生速率。但是,目前连续介质模型在多孔电极中的大规模运用仍存在两个难点:准确描述多孔介质的复杂结构和快速求解含有复杂边界条件的偏微分方程组。因此,多种简化的多孔电极表示方法和经验模型被广泛运用。天然形成的和部分人工制造的多孔介质的微结构具有分形特征,可用分形维数表示。Sakaguchi等[16]利用PNP方程研究了分形多孔电极中的充电过程,并发现分形多孔介质充注过程的时间演化遵循幂律,指数与分形维数有关。目前大量研究都集中在单个孔隙中的充放电过程,因此可以通过等效介质近似(effective medium approximation,EMA)方法[17],用假设的、具有相同导电性的单个孔隙组成的均质网络来替代无序多孔介质的非均质网络中的孔隙,同时保持孔隙网络的连通性。Lian等[18]利用该方法研究了平均孔径、孔径分布和孔连通性对多孔炭电极离子输运特性(包括电导和电导率)的影响。更进一步地,孔隙网络模型(pore network modeling, PNM)采用不同大小的球体和圆柱代表多孔结构中的空腔和吼道[19]。因此,PNM可以考虑多孔电极中的孔径分布和孔道连通性等性质,且计算成本非常低,可以在合理的时间内通过PNP方程计算储能设备的电化学性能和寻找最佳电极结构[20-21]。此外,Lian等[8]报道了一种简单且基于物理的堆叠电极模型来表示多孔电极,成功用PNP方程和等效电路模型解释了超级电容器的缓慢充电动力学,并发现充电过程可以分为两个不同弛豫时间尺度的阶段。虽然上述简化的多孔电极模型被成功运用在解释储能过程中的各种现象,但这些方法只能在一定程度上接近真实的多孔电极的孔径分布,很难表示多样化的表面形态和分布复杂的催化活性位点,因此限制了这些简化模型在多孔电极中的应用。
为了对真实的多孔电极(尤其是非均质、各向异性材料)中的热-质传递过程进行深入的理解,需要对孔隙和骨架结构进行高分辨率三维表示。目前可以通过微尺度X射线计算机断层扫描[22-23](computed tomography, CT)或扫描电子显微镜[24](scanning electron microscope, SEM)以非破坏性的方式获取多孔介质的孔隙结构。但是,CT不能分辨微米以下的结构,SEM的缺点是它只提供二维信息。获得多孔电极的三维结构表示的一种流行的替代方法是随机重构。总地来说,随机重构包括处理可用的信息,并生成符合所导出的介质特性的随机结构两个步骤。基本上有两种重构方法。第一种依赖于基于流程的建模。这种方法试图模拟自然材料在其原始环境中的形成过程[25],或创造工程材料的过程[26]。然而,现有的基于过程的方法只考虑了某些方面,难以准确描述材料结构。一种试图解决这些问题的方法是相场方法[27]。第二种类型的重构方法采用了一种更加数据驱动的方法,并使用了统计数据。这些统计数据主要来自通过图像分割识别出孔隙相和骨架相的各类图片,使用两点统计信息,如自相关或概率函数[28]、线性路径函数[29]和聚类函数[26]。最常用的两点统计量重构方法是模拟退火(simulated annealing, SA)算法[30-32]。与可能非常复杂,并且可能需要大量超参数调优的基于多点统计[33]的方法相反,模拟退火算法的简单性和准确性在实际运用中很有吸引力。Wu等[34]采用SA算法重构商业锂离子电池阴极LiCoO2的三维微观结构,包括活性材料相、孔隙相和添加剂相。重构阴极的表征提供了重要的结构和输运性质,包括两点相关函数、体积比表面积、曲折度和单个相的几何连通性。Habte等[35-36]研究了正极材料的微观结构形态对锂离子电池性能的影响,首先通过模拟退火算法生成了球形电极的结构,然后计算出结构参数并代入阻抗谱经验公式中,最后得到的阻抗值与实验结果符合较好。目前研究大多都停留在多孔电极的重构、孔结构参数[34,37]和等效传递系数[38-39]的计算上,真实多孔结构的形貌和孔隙结构对离子传递和电极导热的影响尚未被研究过。
本文提出一套研究介观尺度下真实多孔电极中的热-质传递的研究框架:首先采用一种基于改进的状态更新的随机重建方法和动态退火系数相结合的模拟退火算法,将图像分割后的二维SEM图重构为真实介观尺度的三维多孔电极,重构生成的多孔电极的结构和真实多孔电极截面上的结构在统计学意义上是一致的,并在此基础上建立真实多孔电极中的离子传递和电极导热模型。
1 研究思路
本文的研究思路如图2所示。通过改进的模拟退火算法和有限元计算,研究了真实多孔电板中的离子传递和电极导热现象。
图2
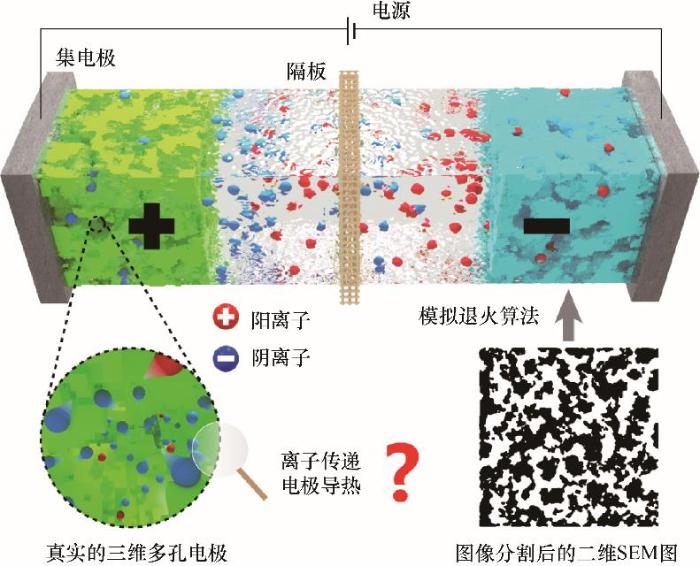
图2 基于模拟退火算法重构的真实多孔电极中的离子传递和电极导热
Fig.2 The ion transport and electrode heat conduction in real porous electrode based on simulated annealing algorithm
2 真实多孔电极的三维重构及其结构参数计算
如图3所示,多孔电极三维重构过程如下:首先利用SEM扫描多孔电极,得到参考图像;然后对其进行预处理,即通过图像分割识别孔隙相和骨架相,得到二值化图像序列,并将二值化图像序列作为参考模型;然后生成与参考模型的孔隙率相同的随机初始点云,利用改进的模拟退火算法进行随机重构,将两点相关函数作为优化目标,采用一种改进的体素交换方法更新状态,得到重构的多孔电极的点云;最后将点云实体化为立方体构成的空隙相和骨架相的结构,并计算了其结构参数。
图3
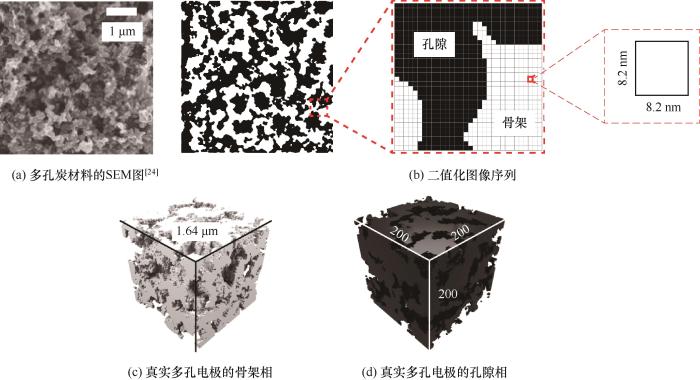
图3 多孔电极三维重构流程图
Fig.3 The flow chart of three-dimensional reconstruction of porous media
2.1 图像预处理
目前研究和应用较多的电极材料主要集中在多孔炭材料、过渡金属氧化物和导电高分子等方面。其中多孔炭材料具有比表面积大、导电性好、结构稳定、资源丰富、价格低廉等优势,既可直接作为电极,又可与其他材料复合,起到传输电子、舒缓体积膨胀以及优化界面反应等作用,被广泛用为电极材料[40]。多孔炭材料的SEM图来自于Kunanusont等[24]的工作,如图3(a)所示。他们采用超临界二氧化碳干燥法,在10.0~20.0 MPa和40℃条件下制备了乙炔炭黑和聚偏氟乙烯基多孔电极,并研究了压力对电极形态、孔隙率和电化学性能的影响。
通过SEM扫描得到的灰度图像序列中,孔隙相和骨架相的灰度值差异明显。因此,首先通过阈值分割算法将灰度图像序列转化为只有孔隙相(黑色区域,灰度值为0)和骨架相(白色区域,灰度值为255)的二值化图像序列。采用SEM图中所有像素的灰度值的平均值(本文为144)作为阈值。当某处的灰度值高于阈值时,则将此处的灰度值设为255;当灰度值小于等于平均值时,则设灰度值为0。处理后的图像中含有斑点噪声和大面积的孔洞,采用形态学运算填充大面积孔洞,同时去除图像中的杂质和亮斑等噪声干扰[41],从而得到预处理之后的二值化图像序列,如图3(b)所示。
2.2 图像结构描述符计算
多孔电极的结构与其结构描述符密切相关,在对多孔电极重构时,需要考虑其结构描述符等信息,使重构模型与参考模型更加符合[42]。采用特征函数
式中,
本文采用的第一个结构描述符是两点概率函数
在平衡态系统中,粒子之间由于相互作用而存在一定的相关性。两点概率函数作为一种常用的结构描述符,可以很好地描述系统的微观结构特征。第二个描述符是两点线性路径函数
2.3 模拟退火算法
模拟退火算法是一种通用的概率优化算法,起源于金属的退火过程,用于在一个很大的搜寻空间中寻找出最优解,可以求解复杂的非线性优化问题。模拟退火算法其实是一种贪心算法,每次都选择一个当前最优解,因此只能搜索到局部的最优值。但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出局部的最优解,达到全局的最优解。
2.3.1 模拟退火算法基本框架
图4是由Yeong等[31]首次提出的模拟退火算法运用在多孔介质重构中的基本框架。首先获得参考模型
图4
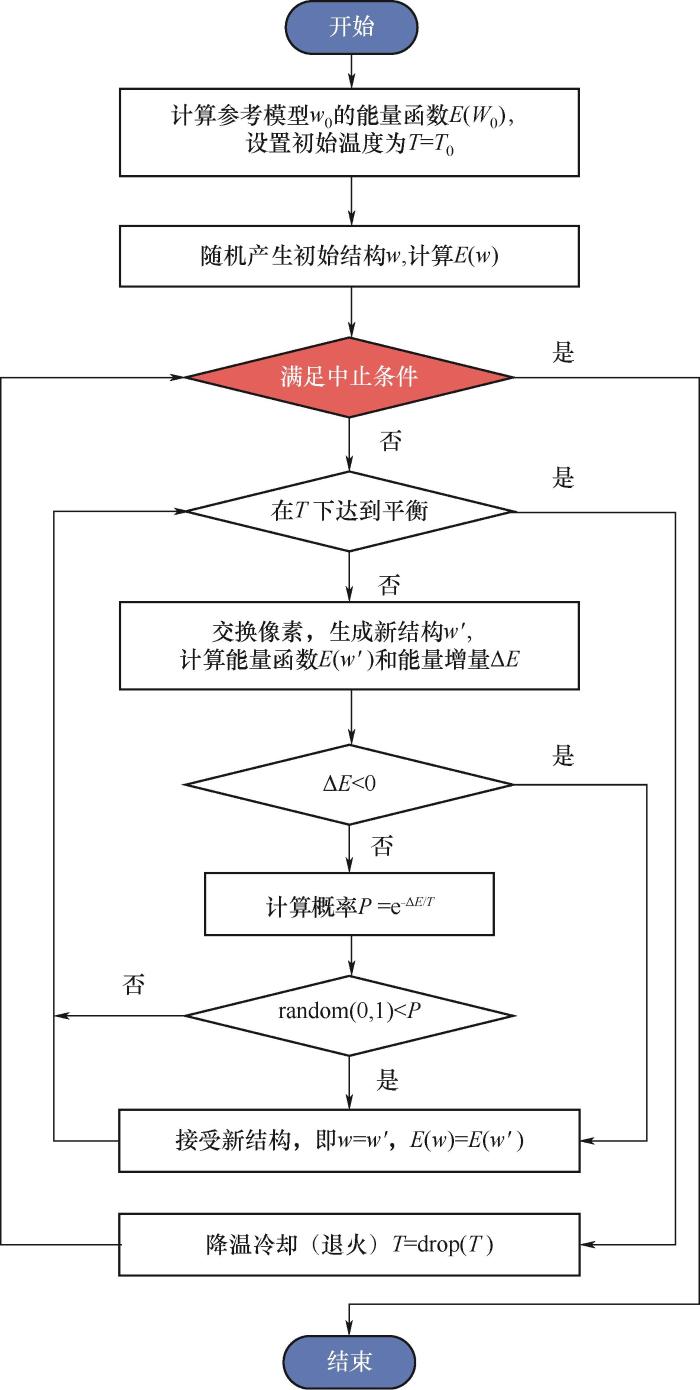
图4 模拟退火算法流程图
Fig.4 The flow chart of simulated annealing algorithm
退出模拟退火算法的条件如下:①系统的能量函数小于阈值
2.3.2 能量函数
原则上,任何结构描述符或描述符的组合都可以用来计算能量函数
式中,d指模型维度。对于二维图像,d包含4个维度,即沿
2.3.3 基于DPN值的像素交换
模拟退火算法的最重要的过程是在保持多孔电极孔隙率
利用传统的随机像素交换方法产生新结构时,图像中所有像素的交换概率相同,这种方法容易破坏已经重构好的局部结构,从而增加了寻找最优结构的时间。同时,图像中孤立的像素点可以被视为噪点,使用传统方法也难以去除。本文引入DPN(different phase neighbors)[43]的概念来改进传统的随机像素交换方法。像素的DPN值指在该像素的邻域内与该像素不同相的像素个数。像素的DPN值反映了该像素在图像中的孤立程度,
图5
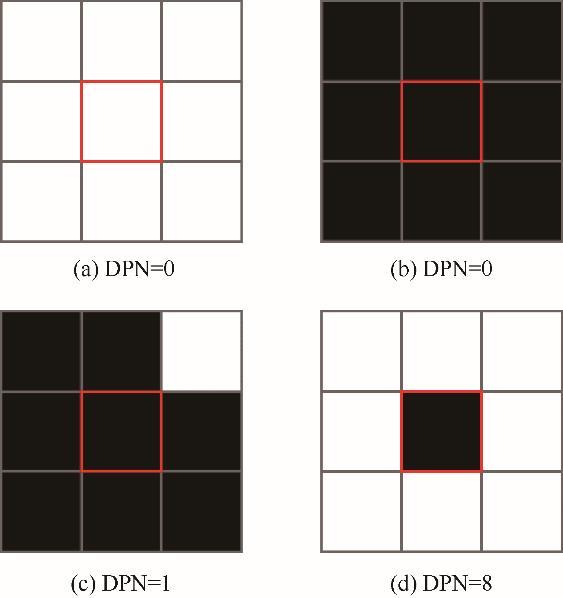
图5 中心像素在不同结构中的DPN值
Fig.5 DPN values of center pixel in different structures
2.3.4 动态退火系数
退火过程就是体系温度下降的过程。温度越低,体系跳出当前解的概率就越低。温度降低太快,容易陷入局部最优;温度降低太慢,算法运行效率太低。因此,为了平衡精度和速度,需要选取合适的退火方法。常用的退火方法为
式中,
2.3.5 参数设置、点云实体化和运行环境
根据前文模拟退火算法的退出条件,设置具体参数如表1所示。
表1 模拟退火算法退出迭代的参数设置
Table 1
| Eth | ΔEth | Ncon | Niter |
|---|---|---|---|
| 1×10-6 | 1×10-8 | 500 | 1×106 |
新窗口打开| 下载CSV
通过模拟退火算法产生的点云无法通过有限元方法模拟其内的离子传递和电极导热过程,需要被实体化为由面构成的三维结构。本文采用Blender自带的API(application program interface),将点云实体化为由小立方组成的多孔电极,最后提取表面结构。图3(c)、(d)分别展示了
本文的计算平台为4 x Intel(R) Xeon(R) Platinum 9242 CPU at 2.30 GHz和384G内存的服务器,模拟退火算法和实体化算法通过Python 3.8编程实现。
2.4 多孔电极的结构参数
孔隙率
多孔电极是分形物质,它的孔隙结构复杂度与其孔隙分形维数等特征参数密切相关。目前常用的计算多孔结构分形维数的方法有盒计数法[45]、豪斯道夫方法[46]和随机游走法[47]。盒计数法由于其精度更高、运算速度更快而被广泛用于计算分形维数。对于多孔电极的孔隙体积
在实际的多孔电极中,孔道的形态一般是弯曲的,离子的传输路径总长度为
所有的结构参数均采用Python 3.8编程计算。表2展示了尺寸分别为
表2 通过模拟退火算法重构的多孔电极的结构参数
Table 2
多孔电极尺寸/ (个立方体) | 边长/ | 结构参数 | |||
|---|---|---|---|---|---|
| 孔隙率 | 比表面积/ | 分形维数 | 曲折因子 | ||
| 0.41 | 0.545 | 1.493×107 | 3.28 | 2.36 | |
| 0.82 | 0.545 | 1.223×107 | 3.19 | 2.01 | |
| 1.64 | 0.545 | 1.306×107 | 3.11 | 2.13 | |
新窗口打开| 下载CSV
3 三维多孔电极中的传质与传热原理
为了研究多孔电极中的传质和传热现象,参考实际超级电容器的工作原理[8],构建了如图6所示的两个模型。受限于计算机的计算资源,离子传递模型采用两个
图6
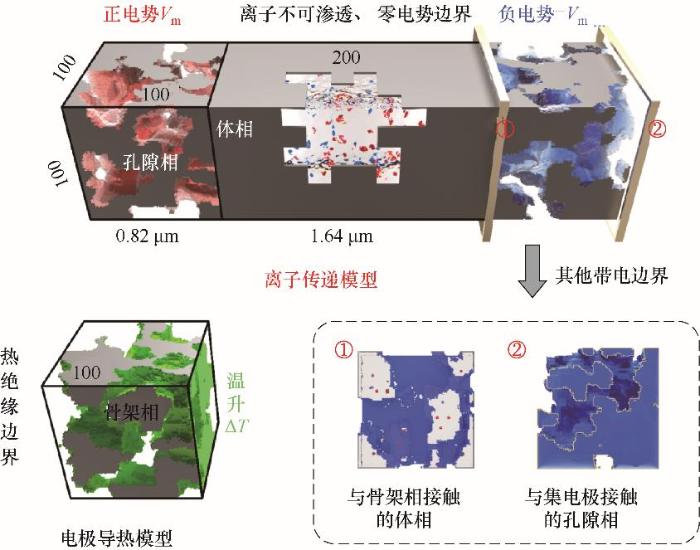
图6 真实多孔电极中的离子传递和电极导热模型
Fig.6 The model of ion transfer and electrode heat conduction in real porous electrodes
3.1 充电过程
刚开始时整个体系的离子密度分布是均匀的,电势为零。当左右两个多孔电极施加相反的电势后,体相和孔隙相中的阴阳离子受到电场力的作用,分别朝着相反的方向定向移动到多孔电极表面,从而形成电流并最终形成双电层(electrical double layer, EDL)储存能量。双电层的厚度通过德拜长度来表示。
式中,
本文考虑到生成的双电层不会发生重叠以及求解的复杂度两个因素,于是采用Poisson-Nernst-Planck(PNP)方程来描述上述复杂孔隙结构中的离子充电动力学。电势
式中,
设由两个多孔电极的孔隙相和体相组成的离子运动空间为
I.C.
式中,
因为多孔炭电极是良好的导体,所以可以假设整个多孔炭电极是一个等势体,即多孔电极和电解液的界面处的电势相等。图6中红色和蓝色区域代表电解液和多孔电极的界面以及电解液和集电极的界面,分别带正电势
B.C.
本文的研究重点是在
本文基于COMSOL Multiphysics 5.4软件,采用有限元法求解上述含有复杂边界条件的PNP方程,从而得到离子在多孔电极中的迁移行为。计算平台为4 x Intel(R) Xeon(R) Platinum 9242 CPU at 2.30 GHz和384G内存的服务器。
3.2 导热过程
在实际的充放电过程中,由于电流的生成和离子的重排等因素[15],整个体系会产生热量。体系温度主要受到热生成、电解液内部的热传导和热对流,以及多孔电极内的热传导影响。而温度又会影响离子的输运参数和电极的导电性能,从而影响整个充电过程。充电、产热和传热三种现象相互耦合,极大地增加了计算量。此外,本文研究体系的电极导热的弛豫时间远小于充电的弛豫时间(或产热的弛豫时间),且模拟时间较短,可以将充电现象和电极导热现象解耦,从而分开研究。因此,为了简化电极导热模型,只考虑电极中的热传导。本文采用傅里叶定律描述热传导过程。
式中,k是热导率,W·m-1·K-1;
设骨架相空间为
热量通过电解液和电极的界面从电解液传入电极中,设电解液和电极的界面为
式中,
Kunanusont等[24]只测量了多孔炭电极的电导率。因此,根据文献[51],设置多孔炭电极的
电极导热过程同样基于COMSOL Multiphysics 5.4软件,采用有限元法求解。计算平台为4 x Intel(R) Xeon(R) Platinum 9242 CPU at 2.30 GHz和384G内存的服务器。
4 三维多孔电极中的传质与传热原理
本节首先验证了改进后的模拟退火算法的高效性,然后模拟了如图6所示的多孔电极模型中的离子传递和电极导热现象。
4.1 改进的模拟退火算法结果
为了验证改进后的模拟退火算法重构的准确性,图7展示了重构结构w的能量函数E(w)随迭代次数的变化曲线。结果表明相较于随机的像素交换策略和静态的退火系数的经典模拟退火算法,采用DPN值的像素交换策略和采用动态的退火系数的改进模拟退火算法在相同的迭代次数下的重构精度更高(即E(w)更小)。但由于每次迭代需要计算每个像素点的DPN值,所以花费的总时间也更长。但是,由于改进的模拟退火算法在每次迭代时E(w)下降的值更大(即斜率更大),所以单位时间内E(w)的减小量可能也更大(即重构效率更高)。
图7
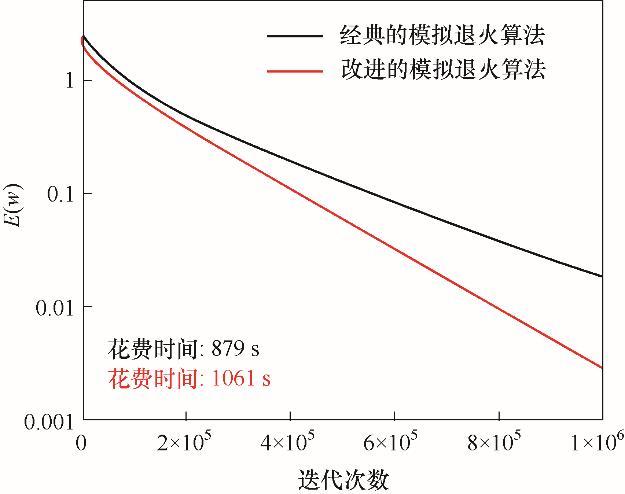
图7 重构结构的能量函数随迭代次数的变化
Fig.7 The energy function of the reconstructed structure varies with the number of iterations
4.2 离子传递
阴阳离子在电势的驱动下,分别朝着正极和负极移动。
图8
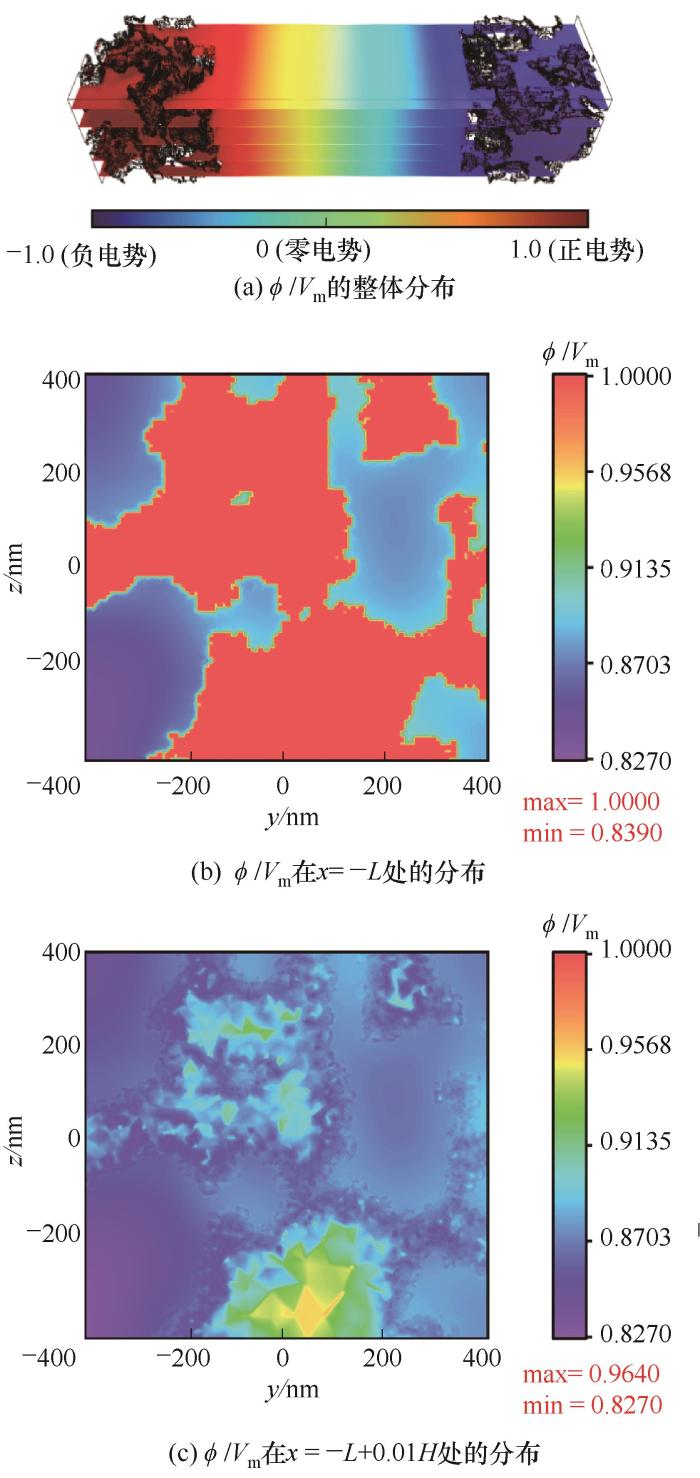
图8
Fig.8 The potential distribution
图9展示了阴阳离子浓度分布的归一化平均值
图9
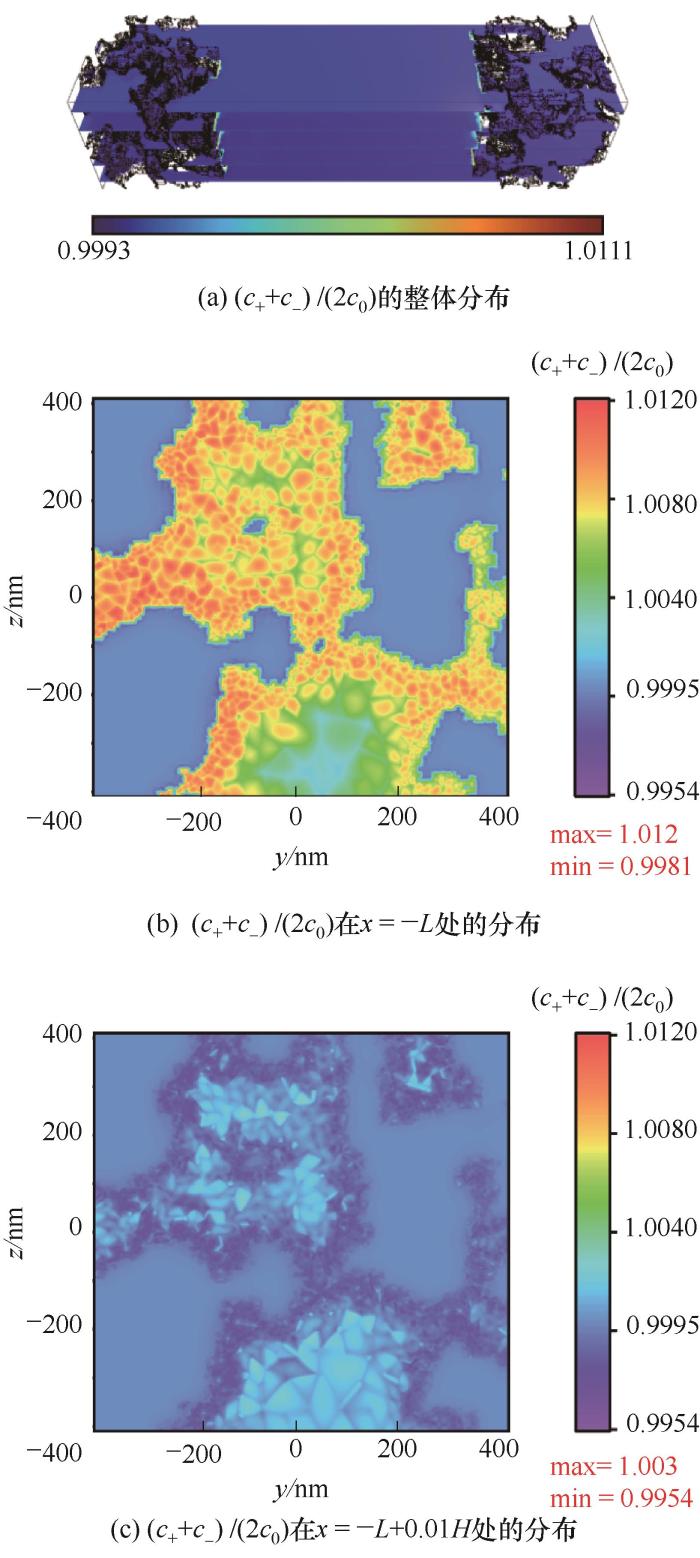
图9
Fig.9 The concentration distribution
4.3 电极导热
图10为多孔电极中的归一化温度分布
图10

图10 不同时刻下的温度分布
Fig.10 Theisosurface diagram of temperature distribution
5 结 论
(1) 一种改进的模拟退火算法重构出的多孔电极结构是稳定且有效的。
(2) 多孔电极内的电势分布不均匀,体相中的电势沿x方向整体线性变化。
(3) 当充电时间为
(4) 由于电解液深入多孔电极内部,导致实际的导热距离远小于多孔电极厚度,于是多孔电极中的热弛豫时间远小于平板的弛豫时间
采用更加真实的物理模型和求解方法用于真实多孔电极中的离子传递和电极导热现象是未来的重点研究方向。PNP方程并没有考虑离子的体积排阻效应,而是假定所有离子是点粒子。离子体积在多孔电极内,尤其是高浓度和高电压时,会极大地影响离子传递现象。为此,Kilic等[52]推导出包含体积排阻效应的MPNP方程。进一步地,为了更全面地弥补连续介质模型在介观尺度下对微观信息的缺失,还可以采用多尺度多物理场经典密度泛函理论代替MPNP方程[7]。目前通过有限元方法求解含有复杂边界条件的偏微分方程组需要消耗大量计算资源,难以深入研究多孔电极结构对热-质传递现象的影响。因此,亟需快速准确求解含有复杂边界条件的偏微分方程组的方法,比如格子Boltzmann方法[53](lattice Boltzmann method,LBM)和神经网络(neural network,NN)[54]。
符 号 说 明
| 热扩散系数,m2·s-1 | |
| 第j相的两点聚类函数 | |
| 骨架相的比定压热容,J·kg-1·K-1 | |
| 分别为阳离子、阴离子的浓度和初始浓度,mol·m-3 | |
| 离子扩散系数,m2·s-1 | |
| 分形维数 | |
| 分别为能量函数、退出迭代的能量阈值、迭代过程中能量函数的最小值和平均值 | |
| 分别为能量增量和退出迭代的能量增量阈值 | |
| 基本电荷, | |
| 电极厚度, | |
| 多孔介质第j相中 | |
| 离子通量,m3·s-1 | |
| 热导率,W·m-1·K-1 | |
| Boltzmann常数,J·K-1 | |
| 体相半长,m | |
| 第j相的两点概率函数 | |
| 孔隙相的传输路径总长度, | |
| 阿伏伽德罗常数 | |
| 分别为连续拒绝随机产生的新结构的次数的上限值和模拟退火算法可以迭代的最大次数 | |
| 孔隙相立方体的数量 | |
| 多孔电极所有立方体的数量 | |
| 法线方向的单位向量 | |
| 电荷数密度,m-3 | |
| 第j相的两点线性路径函数 | |
| 分别为带正电、带负电和不带电的边界 | |
| 分别为局部温度和体系初始温度, | |
| 分别为第k-1、k次迭代时的温度, | |
| 温升, | |
| 时间, | |
| 多孔介质某个相所占的区域 | |
| 热电势, | |
| 孔隙相体积, | |
| w0,w,w′ | 分别为参考模型的二维结构、模拟退火算法的初始三维结构和下一步生成的三维结构 |
| 离子的价态 | |
| 骨架相空间 | |
| 长度尺度, | |
| 相对介电常数,F·m-1 | |
| 真空介电常数,F·m-1 | |
| 分别为温升边界和绝热边界 | |
| 分别为退火系数、退火系数的最小值和最大值 | |
| 德拜长度, | |
| 体相离子数密度,m-3 | |
| 骨架质量密度,kg·m-3 | |
| 曲折因子 | |
| 单板电极中热传导的弛豫时间, | |
| 单板电极中离子传递的弛豫时间, | |
| 电势, | |
| 分别为多孔介质第j相的浓度和多孔介质的孔隙率 | |
| 离子运动空间 | |
| 上角标 | |
| 多孔介质某个相的序号 | |
| 下角标 | |
| av | 平均值 |
| con | 新结构连续被拒绝 |
| f | 骨架相 |
| iter | 迭代 |
| 迭代次数 | |
| min | 最小值 |
| r | 相对 |
| 图像中任意一点的位置 | |
| th | 阈值 |
| - | 带负电 |
| + | 带正电 |
| ± | 阴阳离子 |
- GB/T 7714-2025与GB/T 7714-2015相比,变更了哪些,对期刊参考文献格式有什么影响?
- 别被这个老掉牙的报纸理论版投稿邮箱误导了!最新核实91个报纸理论版投稿邮箱通道,一次集齐
- 喜报!《中国博物馆》入选CSSCI扩展版来源期刊(最新CSSCI南大核心期刊目录2025-2026版)!新入选!
- 2025年中科院分区表已公布!Scientific Reports降至三区
- 国内核心期刊分级情况概览及说明!本篇适用人群:需要发南核、北核、CSCD、科核、AMI、SCD、RCCSE期刊的学者
- CSSCI官方早就公布了最新南核目录,有心的人已经拿到并且投入使用!附南核目录新增期刊!
- 北大核心期刊目录换届,我们应该熟知的10个知识点。
- 注意,最新期刊论文格式标准已发布,论文写作规则发生重大变化!文字版GB/T 7713.2—2022 学术论文编写规则
- 盘点那些评职称超管用的资源,1,3和5已经“绝种”了
- 职称话题| 为什么党校更认可省市级党报?是否有什么说据?还有哪些机构认可党报?

 0373-5939925
0373-5939925 2851259250@qq.com
2851259250@qq.com



