基于平行多种群与冗余基因策略的置信规则库优化方法

作者：徐晓滨朱伟晓健侯平智常雷雷来源：《自动化学报》日期：2022-10-24人气：608

置信规则库(Belief rule base, BRB)是一种基于D-S (Dempster-Shafer)证据理论的复杂系统建模、分析与评价的专家系统方法. 该方法以置信规则(Belief rule)为基础, 能够较好地表示、建模和集成不确定条件下的多种类型信息[1-2]. 同时, 作为一种“白箱(White box)”方法, BRB还具有较强的可解释性, 专家可以更好地参与BRB的建模、训练以及学习过程. 自提出以来, BRB已成功应用于各个领域, 如智慧医疗[3]、多属性决策分析[4]以及军事能力评估[5]等.

然而, BRB的规模不宜过大, 否则将会给建模造成巨大的困难. 同时, 由于人的认知不完备或者数据缺失, 专家给定的初始化BRB可能面临所筛选关键指标及其取值不准确的情况, 因此采用初始BRB进行建模、评估和预测时, 其结果精度可能不高. 为了解决这些问题, 需要对初始BRB进行学习优化以明确其规模和提高建模精度. 众多研究者在多个领域开展了相关研究, 主要可以分为3类: BRB结构学习、BRB参数学习以及BRB结构与参数联合优化.

BRB结构学习的目的是识别与筛选关键前提属性及其参考值. Chang等[5]首先提出了基于主成分分析等维度约减技术的BRB结构学习方法, 对装备体系综合能力评估问题开展了相关研究; Wang等[6]提出动态调整BRB规则的结构学习方法; Li等[7]提出了基于极小方差的前提属性参考值确定方法, 并基于此提出了安全性评估方法.

BRB参数学习的目的是通过优化BRB相关参数的取值以提高建模精度. Yang等[8]提出BRB优化模型优化BRB的参数. Zhou等[9]基于期望极大估计算法提出了在线参数学习方法, 对于时效性有较高要求的复杂决策问题提供了在线建模方法. Chen等[10]对前提属性参考值存在的约束进行分析, 改进了BRB系统的优化模型, 将前提属性参考值作为被训练的参数进行参数学习, 并将原优化模型称为局部训练模型, 改进后的优化模型称为全局训练模型. Savan等[11]、Chang等[12]和马炫等[13]提出了基于演化算法(Evolutionary algorithms, EA)的BRB参数学习方法. Chang等[12]对比了多种演化算法的求解效率, 包括遗传算法(Genetic algorithm, GA)、差分进化(Differential evolutionary, DE)算法以及粒子群(Particle swarm optimization, PSO)算法等. 这些优化算法在解决解空间较大的理论与实践问题方面具有较强的优势.

在结构学习和参数学习的基础上, Chang等[14-16]进一步提出了对BRB参数和结构进行优化的BRB联合优化方法, 通过构建双层优化模型, 在外层模型中优化BRB结构, 在内层模型中优化BRB参数, 实现对BRB参数与结构的联合优化. Yang等[16]提出BRB结构和参数的联合优化方法, 采用启发式策略(Heuristic strategy)优化BRB结构, 采用差分进化算法优化BRB参数.

以上有关BRB结构学习、参数学习的相关工作仅关注单一层面, 而文献[14-16]虽然实现了对BRB结构与参数的优化, 但是其对BRB结构和参数的优化仍然是分别开展, 更具体而言, 在外层模型中仅优化BRB结构, 在内层模型中仅优化BRB参数. 在本质上仍然属于迭代(Iterative)的过程, 并未实现对BRB结构与参数的同时优化.

基于此, 本文提出一种基于平行多种群策略和冗余基因策略的BRB优化方法. 该方法中, 采用具有不同基因数量的多个种群来编码具有不同数量规则的BRB, 多个不同种群共同参与优化过程来实现对BRB结构与参数进行优化的目的; 在优化过程中, 为具有较少基因的个体(具有较少规则的BRB)补充部分冗余基因, 以确保不同长度个体能够同时参与优化过程. 采用该方法, 可以一次产生具有不同数量规则BRB的最优解, 并自动生成帕累托前沿, 决策者可以根据自身偏好或实际问题需求在帕累托前沿上筛选最优解. 最终以某输油管道泄漏检测问题为例对本文提出的方法进行验证.

1. BRB理论基础及推理过程

1.1 BRB基础

在传统D-S证据理论的基础上, Yang等[8]进一步提出采用具有置信结构的IF-THEN规则来表达、建模与推理不确定条件下的多种类型信息, 包括定性定量信息、语义数值信息、完备与不完备信息等. 由具有同一置信结构的IF-THEN规则组合而成的规则库即称为置信规则库(BRB), 其中第 $k$ 条规则如式(1)所示:

\begin{aligned} R_{k} : & i f (x_{1} i s A_{1}^{k}) \land (x_{2} i s A_{2}^{k}) \land \dots \land (x_{M} i s A_{M}^{k}), \\ t h e n {(D_{1}, β_{1, k}), \dots, (D_{N}, β_{N, k}) \\ w i t h r u l e w e i g h t θ_{k} a n d a t t r i b u t e w e i g h t δ_{m} \end{aligned}

(1)

其中, $x_{m} (m = 1, \dots, M)$ 表示第 $m$ 个前提属性, $A_{m}^{k} (m =$ $1, \dots, M; k = 1, \dots, K)$ 表示第 $k$ 条规则中第 $m$ 个前提属性的参考值; $β_{n, k} (n = 1, \dots, N)$ 表示第 $k$ 条规则中第 $n$ 个评估结果 $D_{n}$ 的置信度; “ $\land$ ”表示规则满足交集假设; $θ_{k}$ 和 $δ_{m}$ 分别表示第 $k$ 条规则和第 $m$ 个前提属性的权重.

相应的, 当置信规则建立在并集假设下时, 其表述形式如式(2)所示:

\begin{aligned} R_{k} : & i f (x_{1} i s A_{1}^{k}) \lor (x_{2} i s A_{2}^{k}) \lor \dots \lor (x_{M} i s A_{M}^{k}), \\ t h e n {(D_{1}, β_{1, k}), \dots, (D_{N}, β_{N, k}) \\ w i t h r u l e w e i g h t θ_{k}, a t t r i b u t e w e i g h t δ_{m} \end{aligned}

(2)

其中, “ $\lor$ ”代表规则满足并集假设.

作为一种具有白箱特征的专家系统方法, BRB已经广泛应用于解决多复杂系统问题[17-18].

1.2 BRB的推理

BRB系统的规则推理过程主要有4个步骤.

步骤 1. 计算前提属性与参考值之间的匹配度.

对于给定前提属性 $x_{m}$ 的值为 $x_{m}^{*}$ , 第 $j$ 条规则中第 $m$ 个属性的匹配度如式(3)所示:

φ (x_{m}^{*}, A_{m}^{j}) = {\begin{array}{l} \frac{A_{m}^{k + 1} - x_{m}^{*}}{A_{m}^{k + 1} - A_{m}^{k}}, & j = k (x_{m}^{k} \leq x_{m}^{*} \leq x_{m}^{k + 1}) \\ \frac{x_{m}^{*} - A_{m}^{k}}{A_{m}^{k + 1} - A_{m}^{k}}, & j = k + 1 \\ 0, & j = 1, 2, \dots, | x_{i} |, j \neq k, k + 1 \end{array}

(3)

其中, $x_{m}^{*}$ 代表第 $m$ 个属性的输入值, $A_{m}^{k + 1}$ 和 $A_{m}^{k}$ 表示相邻激活规则中的第 $m$ 个属性的值. 第 $j$ 条规则中的第 $m$ 个属性的综合匹配度如式(4)所示:

α_{m}^{j} = \frac{φ (x_{m}^{*}, A_{m}^{j}) c_{m}}{\sum φ (x_{m}^{*}, A_{m}^{j})}

(4)

其中, $c_{m}$ 表示第 $m$ 个属性的置信度. 如果没有不完整的信息并且第 $m$ 个属性的置信度为1, 则式(4)可以简化为式(5):

α_{m}^{j} = φ (x_{m}^{*}, A_{m}^{j})

(5)

步骤 2. 计算激活规则权重.

第 $k$ 条规则的激活规则权重计算如式(6)所示:

w_{k} = \frac{θ_{k} \prod_{m = 1}^{M} α_{m}^{k}}{\sum_{k = 1}^{K} θ_{k} \prod_{m = 1}^{M} α_{m}^{k}}

(6)

其中, $θ_{k}$ 表示第 $k$ 条规则的相对权重; $α_{m}^{k}$ 表示第 $k$ 条规则中第 $m$ 个前提属性与参考值集合 $x_{m}$ 之间的匹配度. 如果 $w_{k} > 0$ , 表示第 $k$ 条规则被激活, 否则第 $k$ 条规则未被激活.

步骤 3. 通过证据推理(Evidential reasoning, ER)算法融合被激活的规则, 如式(7) (见本页下方)和式(8) (见下页上方)所示. 式(7)和式(8)中, $β_{n}$ 表示第 $n$ 个评估结果的置信度.

步骤 4. 输出结果.

融合相应的规则后得到评估结果的置信分布形式, 如式(9)所示:

\begin{matrix} (9) & U = {(D_{n}, β_{n}) | n = 1, 2, \dots, N} \end{matrix}

(9)

当评估结果输出为单一值时, 需要对步骤3中的结果进行集成. 假设评估等级 $D_{n}$ 对应的效用值为 $U (D_{n})$ , 则评估结果的综合效用 $U$ 可根据式(10)进行计算.

\begin{matrix} (10) & α_{m}^{j} = \frac{φ (x_{m}^{*}, A_{m}^{j}) c_{m}}{\sum φ (x_{m}^{*}, A_{m}^{j})} \end{matrix}

(10)

1.3 BRB学习以及面临的问题

当前BRB的学习方法可大致分为3类:

1) BRB结构学习

BRB结构学习主要思想是缩减BRB规模或者是确定BRB的最佳结构. BRB规模与前提属性的个数以及前提属性的参考值有关[5-7]. 因此, BRB结构学习主要从这两方面考虑. BRB结构学习所解决的是由前提属性的个数或者前提属性的参考值个数过多而导致的组合爆炸的问题.

2) BRB参数学习

BRB参数学习主要思想是优化BRB的参数提高建模精度[8-10]. 由于人的认知不完备或者数据缺失, 专家给定的初始化BRB可能面临所筛选关键指标及其取值不准确的情况, 因此采用初始BRB进行建模、评估和预测时, 其结果精度可能不高. 因此提出BRB参数学习以提高对复杂非线性系统的建模能力. BRB的参数优化模型取均方误差或者绝对误差作为优化目标函数, 前提属性的参考值, 规则权重以及评估结果的置信度作为决策变量. 目前BRB的优化方法主要有主成分分析法(Principal component analysis, PCA)、牛顿法以及演化算法(Evolutionary algorithm, EA).

3) BRB联合优化

BRB联合优化的主要思想是对BRB结构和参数同时优化以减小建模复杂度和提高建模精度[14-16]. 当前针对BRB参数和结构优化的BRB联合优化方法[14-15]中, 首先推导出集成模型精度(由均方差表示)与复杂度(与规则数量相关)的综合优化目标, 然后构建双层优化模型, 并提出基于演化算法的优化模型求解算法, 最终实现对BRB结构与参数的联合优化. 但是该方法对BRB结构与参数的联合优化是迭代进行, 并未实现对BRB结构与参数的同时优化.

β_{n} = \frac{μ [\prod_{k = 1}^{K} (w_{k} β_{n, k} + 1 - w_{k} \sum_{s = 1}^{N} β_{n, k}) - \prod_{k = 1}^{K} (1 - w_{k} \sum_{s = 1}^{N} β_{n, k})]}{1 - μ [\prod_{k = 1}^{K} (1 - w_{k})]}

(7)

μ = {[\sum_{n = 1}^{N} \prod_{k = 1}^{K} (w_{k} β_{n, k} + 1 - w_{k} \sum_{n = 1}^{N} β_{n, k}) - (N - 1) \prod_{k = 1}^{K} (1 - w_{k} \sum_{n = 1}^{N} β_{n, k})]}^{- 1}

(8)

综上所述, 当前BRB学习相关研究中一般仅局限于结构学习或参数学习, 而开展的BRB结构与参数联合优化的过程本质上也是迭代和分别进行, 并未实现对BRB结构与参数同时进行优化的目的. 基于此, 本文提出采用平行多种群策略和冗余基因策略的BRB优化方法, 实现对BRB结构与参数进行同时优化的目的.

2. 基于平行多种群策略的BRB优化模型

2.1 平行多种群策略

当前, 一般采用多种群策略来集成不同算子的优势以解决大规模优化问题[19-22]. 具体而言, 在不同种群中分别采用不同算子进行优化, 在优化过程中进行对比并将其作为下一代分配优化资源的依据, 综合集成多种不同算子的共同优势. 这是由于传统优化问题中并不涉及结构优化. 因此, 在将多种群策略应用于优化算法时, 不同种群中的优化算子不同, 但个体长度(编码格式)仍是相同的. 但这与本文要解决的核心问题有本质区别: 本文研究的出发点是实现对BRB结构和参数的同时优化, 因此在本文采用的多种群策略中, 不同种群中的个体长度(编码格式)不同.

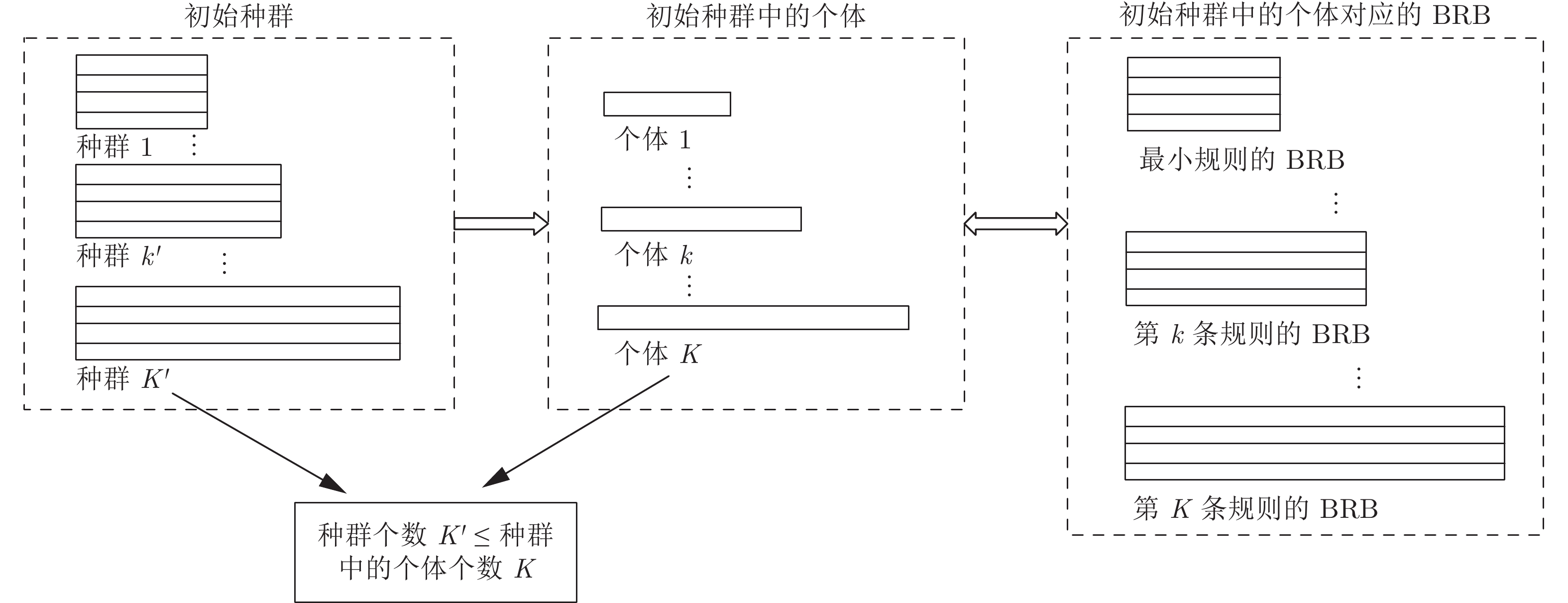
但是, 同时优化BRB结构与参数所面临的最大挑战在于, 具有不同数量规则的BRB规模不同, 而采用演化算法进行求解时, 要求种群中所有个体的长度相同. 本文提出采用平行多种群策略解决这一问题. 将具有不同数量规则的BRB按照其规则数量划分为多个种群, 在单一种群中BRB具有相同数量规则(个体长度相同), 不同种群之间BRB规则数量不同(个体长度不同). 换言之, 将BRB中规则数量 $K$ , 也作为待优化参数之一引入第2.2节中的优化模型中, 以实现对BRB结构与参数同时优化的目的.

图1表示平行多种群策略将初始种群划分为具有不同规则数量的种群(种群规则数量相同), 但仍不能用于交叉变异, 需要添加冗余基因至所有个体长度相等(见第3节).

图 1 平行多种群策略

Fig. 1 Parallel multiple population strategy

下载: 全尺寸图片幻灯片

2.2 BRB优化模型

基于第2.1节提出的平行多种群策略, 建立同时包含BRB结构与参数的优化模型为

\begin{matrix} (11a) & min E (K, A_{m}^{k}, θ_{k}, β_{n, k}) \end{matrix}

\begin{matrix} (11b) & s . t . K_{min} \leq K \leq K_{max} \end{matrix}

\begin{matrix} (11c) & l b_{m} \leq A_{m}^{k} \leq u b_{m} \end{matrix}

\begin{matrix} (11d) & A_{m}^{p} = l b_{m} \end{matrix}

\begin{matrix} (11e) & A_{m}^{q} = u b_{m} \end{matrix}

\begin{matrix} (11f) & 0 < θ_{k} \leq 1 \end{matrix}

\begin{matrix} (11g) & 0 \leq β_{n, k} \leq 1 \end{matrix}

\begin{matrix} (11h) & \sum_{n = 1}^{N} β_{n, k} \leq 1 \end{matrix}

其中, $k = 1, \dots, K; n = 1, \dots, N; m = 1, \dots, M; p \neq$ $q \in [1, \dots, M] .$ 式(11b)表示规则数量在预定的最小规则数 $K_{min}$ 和最大规则数 $K_{max}$ 之间. 式(11c)表示第 $m$ 个前件属性的参考值在下界 $l b_{m}$ 和上界 $u b_{m}$ 之间. 式(11d)和式(11e)表示第 $m$ 个前件属性的参考值的上下界必须包含在规则中. 式(11f)表示初始规则权重应该在 $(0, 1]$ 内. 式(11g)表示评估结果的置信度应该在 $[0, 1]$ 内. 式(11h)表示评估结果的置信度之和小于或者等于1 (当信息不完整时) $\sum_{n = 1}^{N} β_{n, k} < 1$ .

3. 基于冗余基因策略的BRB优化算法

为了求解第2.2节中建立的优化模型, 本节提出基于冗余基因策略的BRB优化算法. 基于冗余基因策略, 对基因数量较少的个体(规则数量较少的BRB)补全部分冗余基因, 至所有个体的长度相等. 这样所有个体的长度即一致, 也就可以参与优化操作, 而并不参与适应度计算.

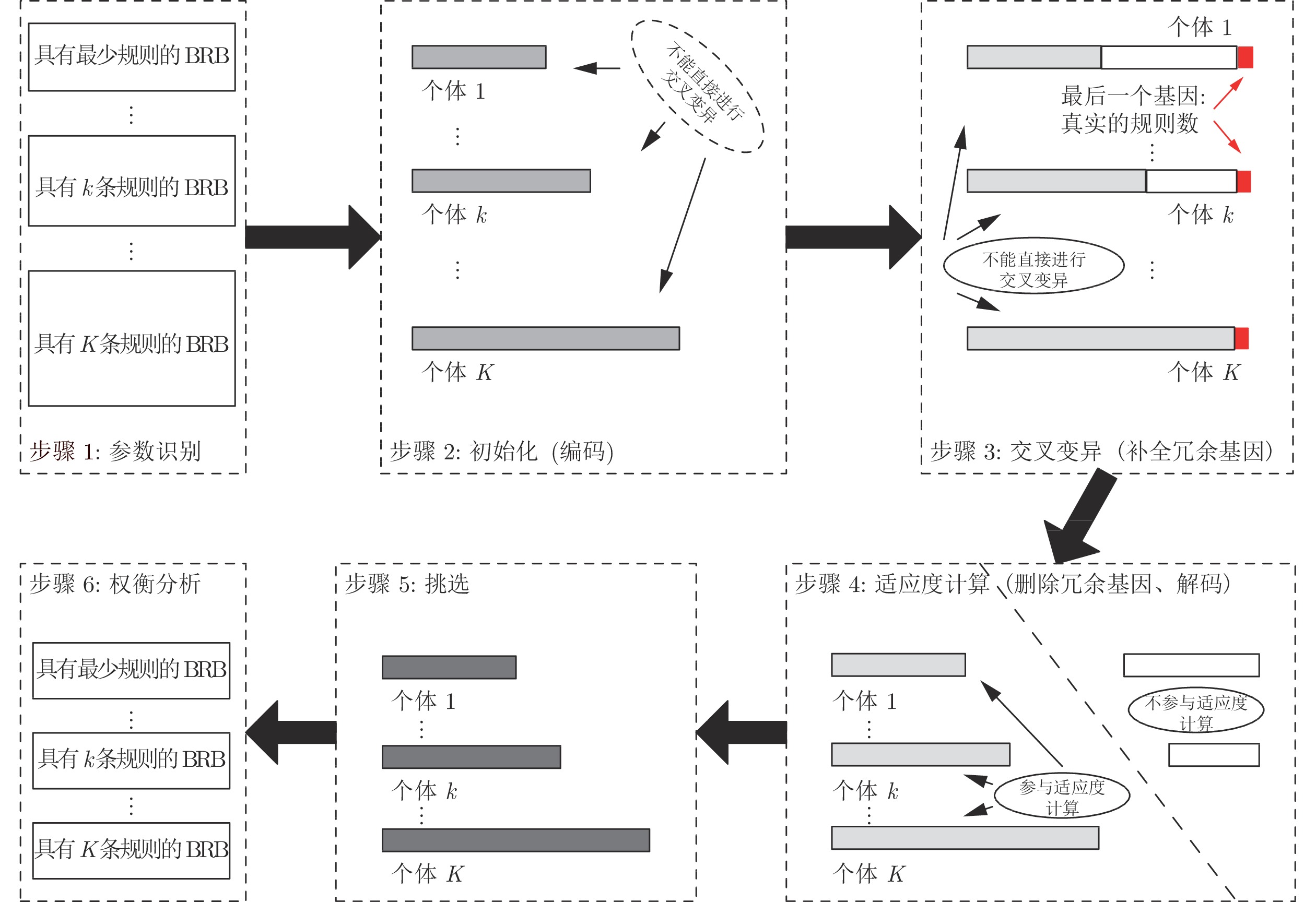
基于冗余基因策略的BRB优化求解算法共包括6个步骤, 如图2所示.

图 2 优化算法的6个步骤

Fig. 2 Optimization algorithm with six steps

下载: 全尺寸图片幻灯片

步骤 1. 参数识别

参数识别主要包括演化算法的参数设值和BRB的参数设值. 演化算法的参数包括种群个数、迭代次数等. BRB的参数包括BRB的规则个数、前提属性(参考值)的个数、评估结果的置信度个数.

步骤 2. 初始化(编码)

每一个个体代表一个具体的BRB. 个体基因由BRB的参数组成. BRB的参数包括前提属性的参考值、规则权重、评估结果的置信度以及表示BRB中规则数量 $K$ . $K$ 的取值为离散整数, 介于最小规则数 $K_{min}$ 和最大规则数 $K_{max}$ 之间.

不同的BRB具有不同的规则数量, 不同个体之间的基因个数也不相等, 这就导致不同种群中的个体长度不同, 因此不能进入下一步的交叉变异操作.

步骤 3. 交叉变异(补全冗余基因)

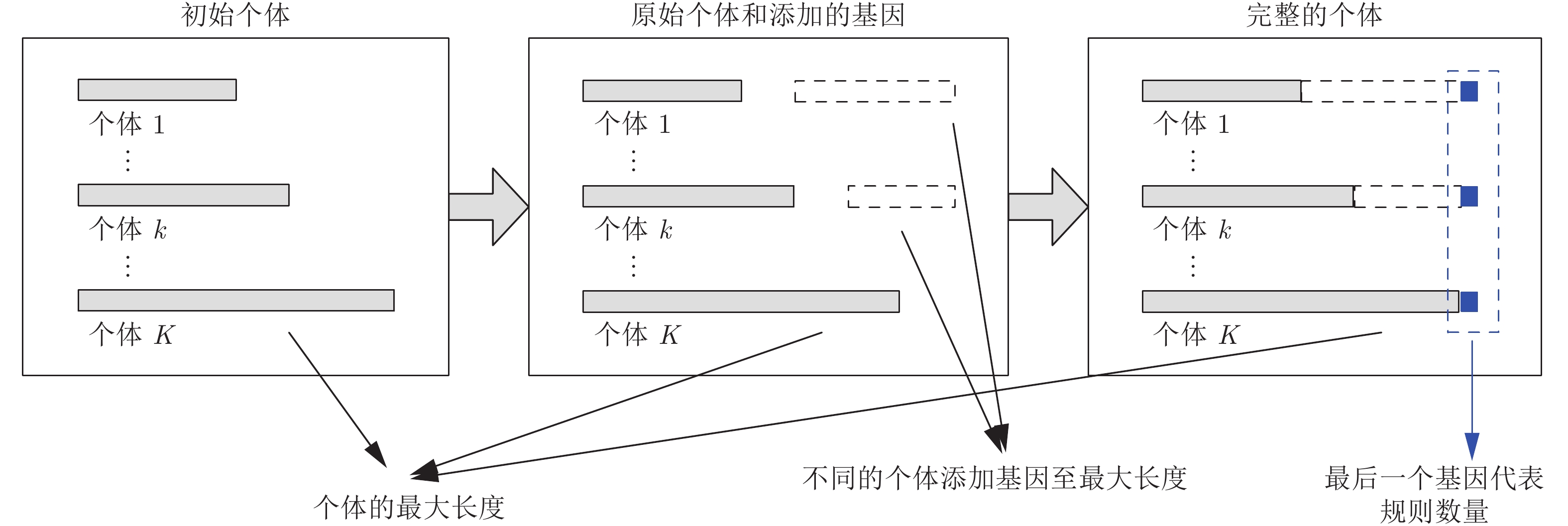
在进行交叉变异操作之前, 首先需要对不同种群中的所有个体补全冗余基因, 以确保所有个体的长度相同(所有个体包含基因数量相同), 如图3所示.

图 3 添加冗余基因

Fig. 3 Add redundant genes

下载: 全尺寸图片幻灯片

向各个个体中补全基因的操作步骤如下: 首先识别具有最多基因数量的个体(即具有最多规则数量的BRB), 以该个体的长度为标准长度; 然后依次对每个个体补全冗余基因, 需要注意补全基因应当满足所在位置的上下限要求, 且最后一位标志初始规则数量的基因 $K$ 位置和取值不变.

补全基因后, 所有个体长度将会相等, 均为初始具有最多基因数量个体的长度. 补全基因后个体将进入优化操作. 本文采用的是差分进化[19-21]算法作为优化引擎, 其优化操作包括交叉和变异.

交叉策略指出引入交叉算子可以增强种群的多样性. $v_{i, j}^{'}$ 为第 $j$ 个基因的临时个体即交叉后的个体, 其交叉算子为 $C R$ , $z_{i, j}^{'}$ 是当前个体, 其交叉算子为 $1 - C R$ . 每一个个体按照一定的概率选择交叉个体 $v_{i, j}^{'}$ , 否则生成原来的个体 $z_{i, j}^{'}$ .

\begin{matrix} (12) & u_{i, j}^{'} = {\begin{cases} v_{i, j}^{'}, 若 r a n d \leq C R 或 j = s n \\ z_{i, j}^{'}, 否 则 \end{cases} \end{matrix}

其中, 交叉算子 $C R = 0.9$ , $s n \in [1, 2, \dots, n]$ 是由每一个个体产生的随机整数.

变异操作指出随机选取种群中两个不同个体, 将其与待变异的个体进行合成, 得到新的个体. 第 $i$ 个新个体 $v_{i}^{'}$ 可以由式(13)得到

\begin{matrix} (13) & v_{i}^{'} = z_{r 1} + F \times (z_{r 2} - z_{r 3}) \end{matrix}

(13)

其中, $z_{r 1}$ , $z_{r 2}$ 和 $z_{r 3}$ 是3个随机产生的个体, 并且 $r 1 \neq r 2 \neq r 3$ , 变异算子 $F = 0.5$ .

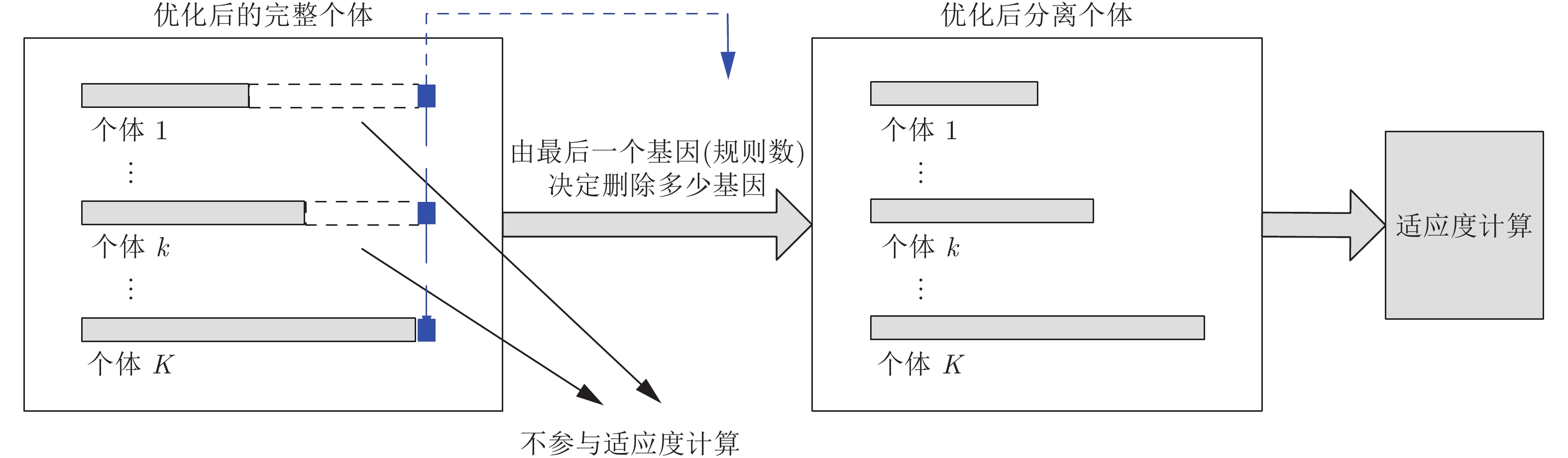
步骤 4. 适应度计算(删除冗余基因、解码)

经过交叉, 变异操作后的个体中的基因已经得到优化, 在进行适应度计算之前需要首先根据每个个体最后一位标志初始长度的基因 $K$ 删除在步骤3中添加的冗余基因, 换言之, 只有与初始BRB相关的基因才会进入适应度计算当中, 步骤3中添加的冗余基因不参与适应度计算, 如图4所示.

图 4 删除冗余基因

Fig. 4 Remove redundant genes

下载: 全尺寸图片幻灯片

删除冗余基因之后, 根据基因编码方案对剩余个体的基因进行解码操作, 然后进入适应度计算, 包括输入信息与前提属性的匹配度计算, 规则激活权重计算以及激活规则集成(见第1.2节).

步骤 5. 选择

通过比较个体的适应度值, 选择适应度值最小的个体作为最优个体作. 在选择适应度值的过程中, 个体适应度值的比较仅局限于具有相同长度的个体或者具有相同规则数量的BRB. 最终的最优个体是由不同规则数量的BRB组成, 而不是由特定数量规则的BRB组成.

对于第 $i$ 个个体 $u_{i}^{t}$ , 选择个体的适应度函数获得更低的额定值作为下一代.

\begin{matrix} (14) & z_{i}^{t + 1} {\begin{array}{l} u_{i}^{t}, 若 f (u_{i}^{t}) \leq f (z_{i}^{t}) \\ z_{i}^{t}, 否 则 \end{array} \end{matrix}

(14)

其中, $f (\cdot)$ 是适应度函数, 本文中是指均方差(Mean square error, MSE).

步骤 6. 权衡分析

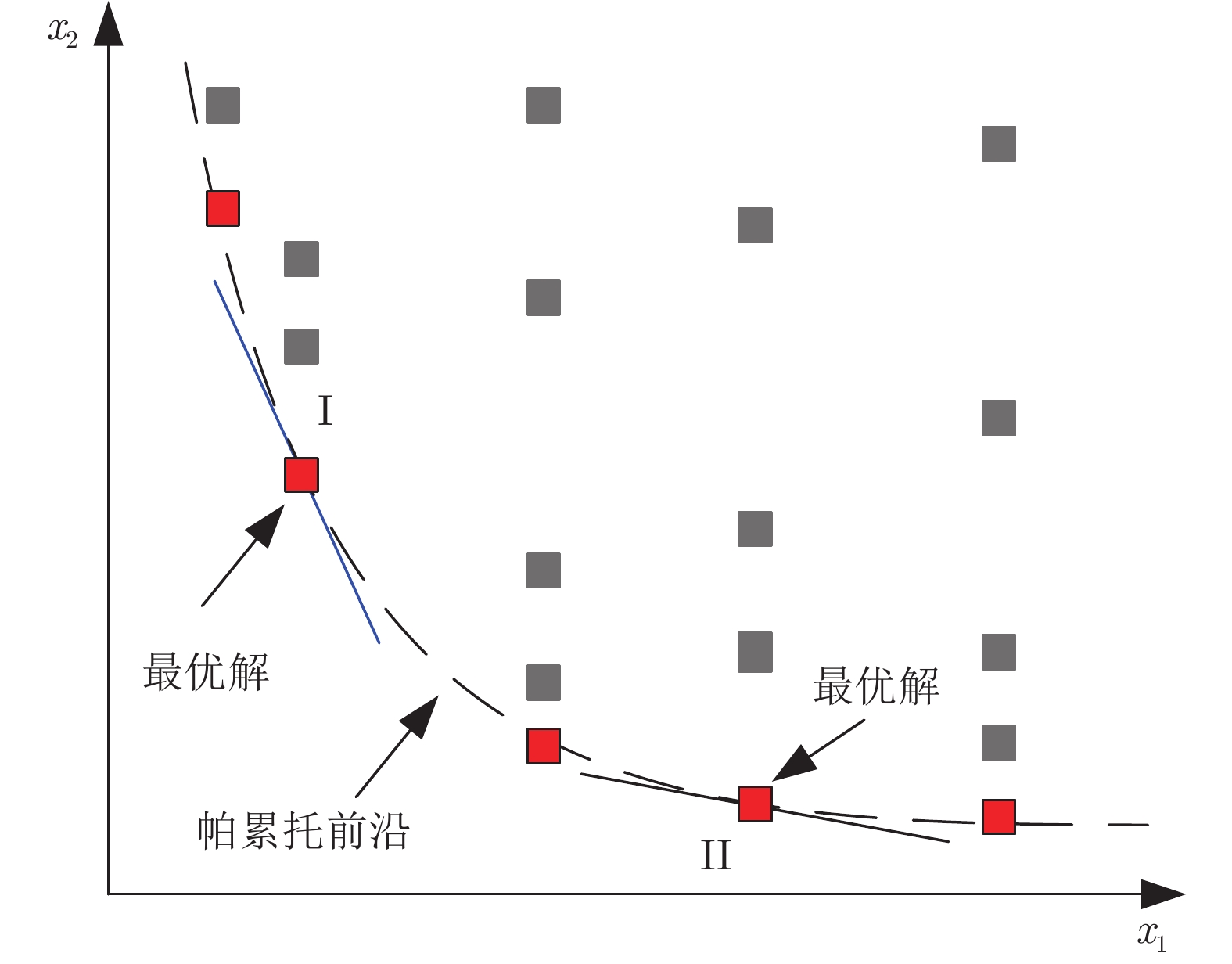
在选择最优的个体之后, 利用具有不同规则数量的最优BRB导出帕累托前沿, 通过考虑决策者的偏好和具体要求, 进行权衡分析以产生最优解.

图5说明了具有两个属性 $(x_{1}, x_{2})$ 问题的权衡分析概念[23]. 图5表示包含两个属性 $(x_{1}, x_{2})$ 的帕累托前沿; Ⅰ点表示偏好 $x_{2}$ 的情况下决策者选择的解决方案; Ⅱ点表示偏好 $x_{1}$ 的情况下决策者选择的解决方案.

图 5 权衡分析

Fig. 5 Tradeoff analysis

下载: 全尺寸图片幻灯片

4. 案例分析

本节以输油管道泄漏检测为例, 验证本文中所提出方法的有效性. 已知可以根据输油管道进出口的流量差(FlowDiff)和压力差(PressureDiff)推断出输油管道的泄漏尺寸值(Leaksize). 流量差和压力差是检测管道中是否存在泄露并且与泄漏尺寸相关的两个重要属性. 因此选择流量差和压力差作为BRB的前提属性, 泄露尺寸作为输出结果. 为了便于对比分析, 本文采用现有BRB相关文献中多次使用的实验数据[9-10, 24], 该数据共包括从英国北部某地采集得到的2008组输油管道泄露数据.

为了与当前方法的进行公平比较, BRB的参数设置与当前方法保持一致. 首先构建BRB的模型, BRB采用5个评估等级评估管道泄漏情况, 其效用值分别为

\begin{matrix} (15) & D_{1}, D_{2}, D_{3}, D_{4}, D_{5} = {0, 2, 4, 6, 8} \end{matrix}

(15)

前提属性流量差 $F l o w D i f f \in [- 10, 2]$ , 压力差 $P r e s s u r e D i f f \in [- 0.02, 0.04]$ .

本文研究的主要目的是实现BRB结构和参数的同时优化, 平行多种群与冗余基因策略适用于演化算法, 如差分进化算法(DE), 遗传算法(GA), 粒子群算法(PSO)等. 在众多优化算法中, DE算法取得了较好的优势, 即其具有优化效率高, 求解速度快且不易陷入局部最优解等优点. 因此本文采用DE作为BRB结构与参数优化模型的求解算法, 为了与当前方法进行比较, DE优化算法的参数值和当前方法使用的参数值一致, 其设置如下:

1) BRB中规则数量取值范围为3 ~ 8条;

2) 优化算法中个体数量设定为100; 迭代次数为1000代;

3) 交叉率和突变率设值为0.8和0.8;

4) 算法共运行30次以验证平行多种群与冗余基因策略方法的稳定性.

表1给出了算法运行30次之后具有不同数量规则的BRB统计结果. 通过表1可以发现, 当规则数量为3 ~ 8条时, 不同BRB的最小值/平均值都远小于其方差(小一个数量级), 这说明本文提出的方法具有较好的稳定性.

表 1 运行30次的数据结果

Table 1 Statistics of 30 runs

	第 3 条	第 4 条	第 5 条	第 6 条	第 7 条	第 8 条
min	$4.0389 \times 10^{1}$	$3.2065 \times 10^{1}$	$2.9210 \times 10^{1}$	$2.9208 \times 10^{1}$	$2.9200 \times 10^{1}$	$2.9189 \times 10^{1}$
avg	$5.3796 \times 10^{1}$	$3.9717 \times 10^{1}$	$3.7355 \times 10^{1}$	$3.7332 \times 10^{1}$	$3.6770 \times 10^{1}$	$4.4892 \times 10^{1}$
vara	$9.5350 \times 10^{2}$	$5.2327 \times 10^{2}$	$3.4741 \times 10^{2}$	$3.2595 \times 10^{2}$	$4.3643 \times 10^{2}$	$2.4779 \times 10^{2}$

下载: 导出CSV

| 显示表格

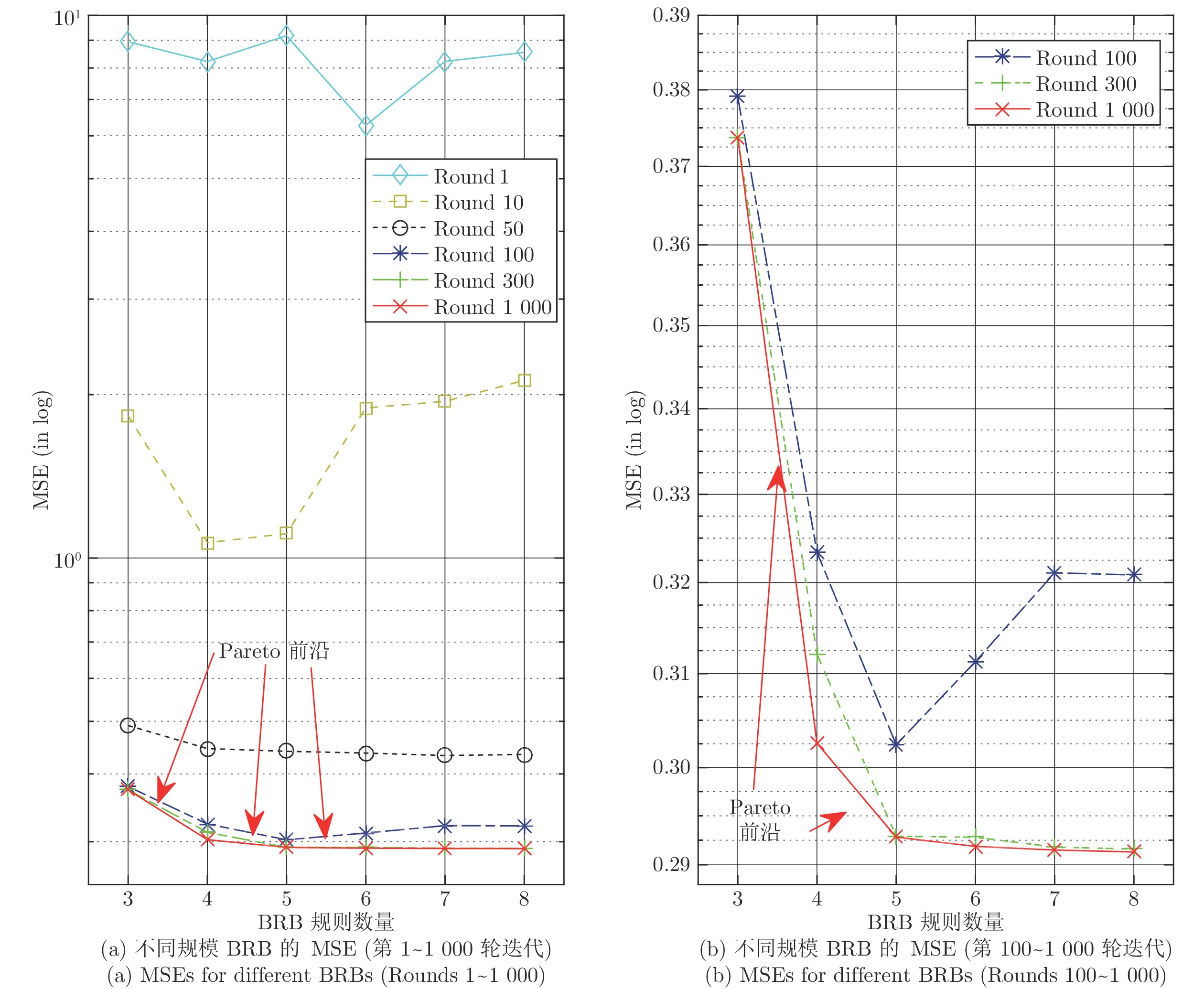
图6进一步给出了本文提出方法在1000代优化过程中帕累托前沿的优化过程.

图 7 输油管道泄漏检测结果与误差对比

Fig. 7 Pipeline leak detection test results and error comparison

下载: 全尺寸图片幻灯片

通过表1以及图6, 可以得出以下结论:

图 6 帕累托前沿的优化过程

Fig. 6 Optimal process of the Pareto frontier

下载: 全尺寸图片幻灯片

1) 在1000代的优化过程中, 帕累托前沿不断向前推进;

2) 当优化至100代时(见图6(b)), 具有不同数量规则的BRB实际上已经达到了比较稳定的可行解;

3) 规则数量(即参数数量)对优化结果具有一定影响. 当优化到100代时, 由于规则数量较多的BRB的参数数量较多, 此时具有6/7/8条规则的BRB并未取得较优解, 也未在帕累托前沿上;

4) 决策者可以根据自身偏好在帕累托前沿上选择最优BRB. 当不考虑偏好时, 具有5条规则BRB具有明显优势, 其MSE明显小于前者, 而后续随着规则数量增加, MSE也并未明显大幅下降, 即具有5条规则的BRB处于拐点(Elbow point)[25].

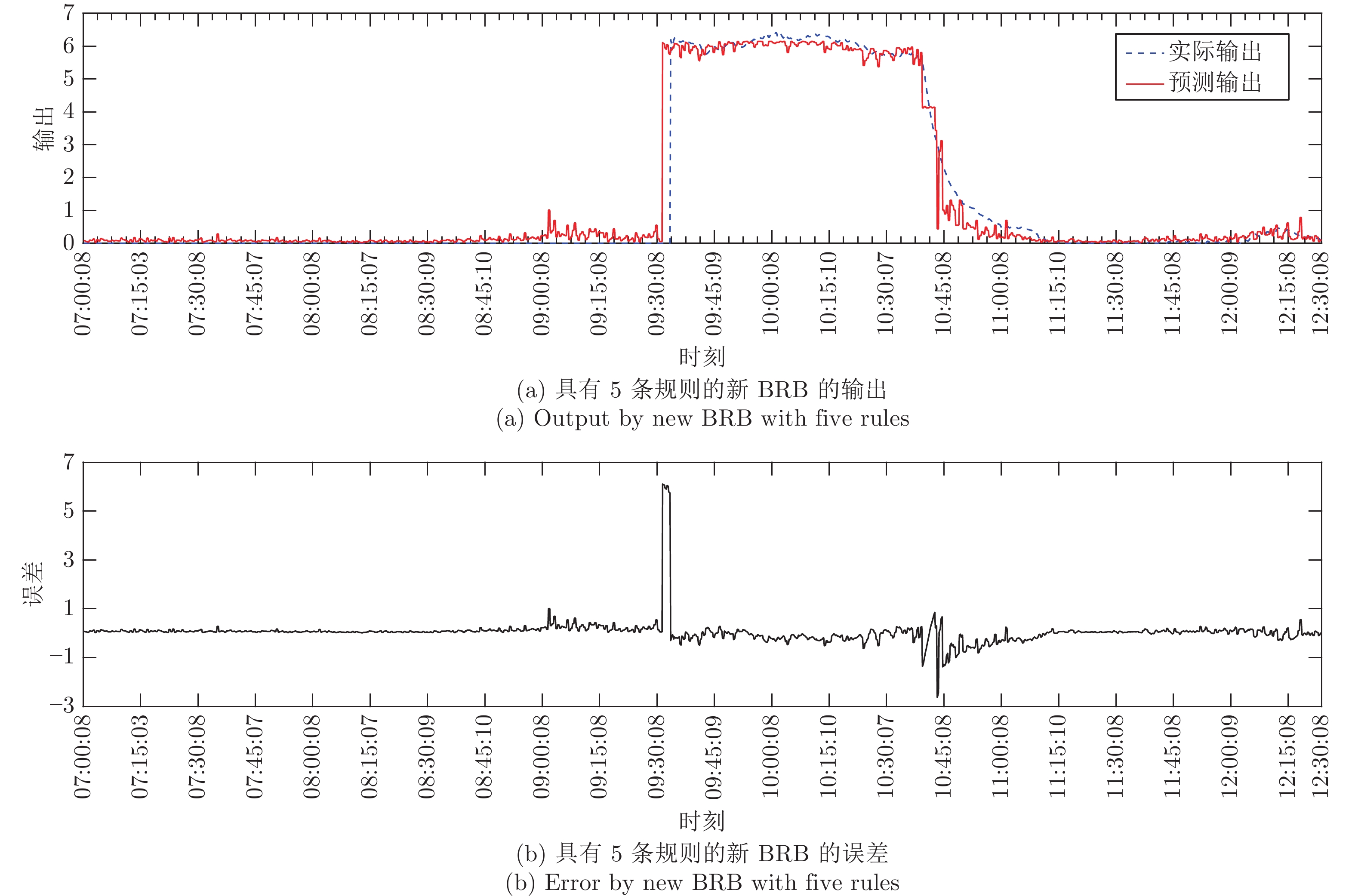
表2给出了具有5条规则的BRB, 图7给出了模型预测结果与真实值之间的对比以及误差.

表 2 具有5条规则的最优BRB参数

Table 2 Optimal BRB parameters with five rules

序号	权重	前提属性		泄露大小
序号	权重	流量差	压力差	0	2	4	6	8
1	0.8642	$- 10.0000$	$- 0.002$	0.3950	0.0692	0.0194	0.0122	0.5042
2	1.0000	$- 7.5000$	$- 0.0176$	0.7878	0.2109	0.0001	0.0000	0.0012
3	0.0911	$- 1.7830$	0.0065	0.0101	0.1245	0.0525	0.5794	0.2335
4	0.2838	0.384 5	0.0073	0.2013	0.2072	0.1513	0.2164	0.2238
5	0.2499	2.000 0	0.0400	0.6588	0.0498	0.0929	0.0243	0.1742

下载: 导出CSV

| 显示表格

表3进一步对比了本文所得结果与已有文献中针对该示例的计算结果. 通过对比, 可以发现:

表 3 基于不同BRB优化方法的实验结果对比分析

Table 3 Comparative analysis of experimental results based on different BRB optimization methods

序号	方法	描述	MSE (MAE)	尺寸(训练/测试)	NOR	NOP
1	其他方法	ANFS	0.5073		9	/
2	其他方法	SVM	0.4219			C = 10, $δ^{2} = 1$
3	以前 BRB 学习方法	局部训练[24]	0.4049	500/200 8	56	336
4		在线更新[9]	0.7880	800/200 8	56	336
5		适应性学习[10]	0.3990	500/200 8	56	349
6		动态规则调整[6]	0.5040	900/200 8	14	108
6		动态规则调整[6]	0.4450	900/200 8	6	39
7		双层优化[15]	0.2917	500/200 8	5	36
8		一般并集 BRB 优化[26]	0.3741	500/200 8	3	20
			0.2848		5	36
			0.2679		12	92
9	本文方法	平行多种群与冗余基因	0.4038	500/200 8	3	240
9	本文方法	平行多种群与冗余基因	0.2921	500/200 8	5	240
注: “NOR”表示规则数量 (Number of rules), “NOP”表示参数数量 (Number of parameters)

下载: 导出CSV

| 显示表格

1) 与已有仅开展参数学习的研究[9-10, 24]相比, 根据不同的优化模型, BRB参数学习的优化参数数量为336 ~ 349. 其模型误差MSE均处于较高水平. 文献[6]提出动态优化方法, 该方法涉及到的优化参数个数从349降到39. 其在降低建模复杂度方面与上述3种方法相比取得了较好的结果. 而本文采用的并行多种群与冗余基因策略的方法取得的模型误差MSE更小, 即本文提出方法相对参数学习具有优势.

2) 本文所得结果稍劣于BRB联合优化方法[14]所得到的结果. 原因在于: BRB联合优化方法属于迭代方法, 即在对BRB参数进行优化时, 并不优化其结构, 而本文提出的方法在一次优化过程中同时实现对BRB结构和参数的优化. 换言之, 在给定资源条件下, BRB联合优化仍然仅优化其参数(这是由其迭代优化的本质决定的), 而本文所提出方法可以同时实现对BRB结构与参数. 在这种情况下, 本文提出方法仍能取得与当前最优解(0.2679)十分接近的结果(0.2921)验证了本文提出方法的有效性.

3) 相比BRB联合优化方法, 本文的另一优势在于最终产生的结果以帕累托前沿的形式表示出来, 决策者既可以根据自身需求或问题特点在帕累托前沿上选择恰当的最优解, 又可以在不考虑偏好的情况下, 根据拐点原则通过权衡分析选择无偏最优解.

5. 结束语

为了实现对置信规则库结构和参数同时优化的目的, 本文提出一种基于并行多种群与冗余基因策略的置信规则库优化方法. 通过输油管道泄漏检测的例子验证本文所提出方法的有效性. 主要结论如下:

首先, 通过并行多种群策略, 具有不同规则数量的BRB可以同时进入优化操作, 因此可以同时优化BRB的结构和参数. 然后, 通过提出冗余基因策略, 具有不同长度的个体(BRB具有不同的规则数量)可以进行交叉变异操作. 只有与初始BRB相关的基因才会进入适应度计算当中. 最后, 输油管道泄漏检测的例子结果表明, 基于并行多种群与冗余基因策略的置信规则库优化方法可以同时优化具有不同规则数量的多个BRB, 随着BRB的优化, 帕累托前沿不断向前推进. 最后可以通过拐点原则识别最佳BRB, 也可以根据决策者的偏好来决定最佳BRB. 下一步工作, 需要对优化算法引擎展开进一步的研究. 优化算法引擎需要大量的参数, 这将导致优化效率下降. 所以迫切需要找到更好的优化技术去解决这些问题. 此外, 还应当在更多理论和实际问题中对本文提出方法进行验证.

关键字：优秀论文

上一篇：基于改进自适应k均值聚类的三维点云骨架提取的研究
下一篇：聚酰亚胺基气凝胶材料的制备与应用

栏目分类

热门排行

推荐信息

期刊知识