精细搜索策略应用于质量交换网络综合

作者：杨岭崔国民周志强肖媛来源：《化工学报》日期：2022-11-03人气：690

随着能源与环保问题日益严峻，我国提出了“碳达峰·碳中和”的战略目标[1]，这对企业降低排放的能力提出新的要求，使得发展新的节能减排和清洁生产技术成为当下的研究热点。质量交换网络(mass exchange network, MEN)[2]作为一项广泛应用于化工原料的提纯、萃取、吸附和污染物去除技术，可显著降低废水、废气的产生和质量分离剂(mass separating agent, MSA)的消耗，近年来受到越来越多的关注。

质量交换网络的概念由El-Halwagi等[3]于1989年提出，是在换热网络研究的基础上发展而来的，因此许多学者[4-6]将换热网络的夹点法与数学规划法运用到质量交换网络上。El-Halwagi等[3]率先使用热力学夹点法设计质量交换网络，在浓度区间表中确定夹点，以此确定具有最大质量交换量的初始网络，并根据初始网络改进为成本最低的网络。Hallale等[7-8]提出了一种新的y-y*复合曲线图，用于处理涉及夹点同一侧存在多个MSA的问题，并指出质量交换单元数量最小并不一定使成本最低，网络设计时应充分考虑传质驱动力。Gadalla[9]将夹点分析原理与质量交换网络联系起来，绘制富流股浓度与等效贫液流浓度的对比图，所得图用于分析当前网络的性能，并设计新的网络结构。Yanwarizal等[10]通过构建浓度与质量负荷图同步确定最小MSA用量和贫富流股间的传质负荷。

此外，数学规划法在质量交换网络综合上也有着广泛的应用。El-Halwagi等[11]使用两阶段合成方法，第一阶段使用线性规划确定外部MSA的最低成本和夹点，第二阶段使用混合整数线性规划减少质量交换器的数量，从而获得综合费用最低的网络结构。Isafiade等[12]提出了一种基于区间的混合整数非线性规划(mixed integer and non-linear programming, MINLP)超结构模型，可同时利用超结构与夹点技术的优点，此外，还规定了分流必须以等浓度混合，虽然简化了模型的复杂度，但一定程度上限制了模型的求解域。李绍军等[13]建立了基于分级超结构的无分流质量交换网络MINLP模型，并采用Alopex算法与遗传算法结合的混合算法进行求解，可同时权衡操作费用和投资费用。谢会等[14]建立了一种基于区间的无分流超结构模型，其中过程贫流股与外部贫流股具有同等匹配机会，且允许重复匹配产生，并将列队竞争算法应用于该模型。都健等[15]以传质浓度差作为优化变量，并考虑了多组分系统，利用改进的遗传算法进行求解，取得了较好的优化结果。侯创等[16]在数学模型中引入了取整函数，并通过LINGO求解器求解，解决了理论塔板数和实际塔板数存在差异的问题，提高了塔板的利用效率的同时降低了年综合费用。

启发式算法与MINLP问题的适应性和强大的搜索能力在许多研究中得以验证，但其难以兼顾全局搜索和局部搜索，一定程度上限制了启发式算法的求解能力。鉴于此，提出一种新的应用于质量交换网络的精细搜索策略，分别利用了启发式方法简单有效、求解域大的特点和确定性方法精度高、收敛快的特点，建立两种精细搜索方式，分别为带有个体回代与分化的高精度强制进化随机游走算法(random walk algorithm with compulsive evolution, RWCE)，以及坐标轮换法与黄金分割法结合的方法。最后通过两个算例验证了两种精细搜索方法的有效性。

1 数学模型

1.1 问题描述

根据目标组分的浓度不同，将过程流股分为贫流股和富流股。为了使富流股中的组分浓度满足出口浓度要求，通过质量分离器将富流股中所含目标组分通过吸收、解吸、吸附、萃取、离子交换等方式转移到贫流股中。质量交换网络优化的目的是在满足出口浓度要求以及传质可行性的前提下，获得最具经济性的网络结构。

如图1所示，贫富流股之间的连接线表示传质单元，并假设为逆流布置。第ir股富流股和第il股贫流股进行传质操作，富流股从进口浓度y $i r i n$ 降低至出口浓度y $i r o u t$ ，贫流股从进口浓度x $i l i n$ 升高至出口浓度x $i l o u t$ 。M表示质量交换量，可由富流股的进出口浓度差与流量Gir 的乘积求得，亦可用贫流股浓度差与流量Lil 求得。

图1

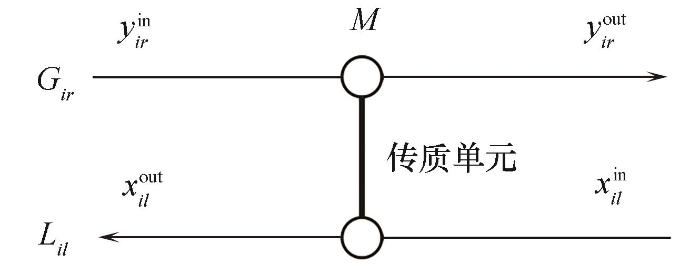
图1 质量交换网络示意图

Fig.1 Sketch map of mass exchange network

贫富流股之间的传质存在相平衡关系，如式(1)所示，对于稀溶液，在所涉及浓度范围内，可假设相平衡关系是线性的，且与富流股中其他可溶性物质无关。

$y_{i r}^{*} = m_{i r, i l} x_{i l} + b_{i r, i l}$ (1)

式中，xil 为贫流股的浓度，此时能与贫流股传质的富流股的最小浓度为Δy $i r *$ ；m和b为与贫富流股的性质有关的常数。图2表示传质过程中富流股的浓度变化以及贫流股的平衡浓度变化。其中Δy表示富流股浓度差；Δy*表示贫流股的平衡浓度差；Δyleft和Δyright分别为传质单元两端的传质驱动力。

图2

图2 贫富流股的相平衡关系

Fig.2 Phase equilibrium of rich and lean stream

1.2 目标函数

目标函数是获得质量交换网络的最低年度综合费用(total annual cost, TAC)，包括质量交换器的投资费用C1和外部贫流股的操作费用C2，如式(2)所示。操作费用取决于外部贫流股的流量，而对于不同工况的分离方式，投资费用计算方式不尽相同。当使用板式塔时，通过增加塔板数来增加质量交换器的传质能力，此时的投资费用由塔板数决定，而使用填料塔时，投资费用由质量交换器的质量决定。操作费用如式(3)所示，投资费用具体计算方式在算例验证部分详细介绍。

$m i n T A C = C_{1} + C_{2}$ (2) $C_{2} = \sum_{i l = 1}^{N L} C_{0} L_{i l}, i l \in N L$ (3)

1.3 有分流节点非结构模型

以往的研究中常采用分级超结构(stage-wise superstructure, SWS)模型[17]合成HEN、MEN，而本文基于换热网络优化的思想，将有分流节点非结构模型(nodes-based non-structural model, NNM)[18]应用于质量交换网络的优化，该模型以节点表示传质单元潜在的位置，具有更强的灵活性和更宽广的求解域。模型如图3所示，结构中有NR股富流股和NL股贫流股，箭头表示流股流动方向，所有质量交换单元均为逆流布置。富/贫流股上分别设置NRG和NLG个分流组，富/贫流股经过每个分流组时，分裂为NRS和NLS个分流，该组所有的分流在末端进行非等浓度混合后流入下一分流组。每个分流分别包含NRD和NLD个节点，因此所有的富流股节点数为NR×NRG×NRS×NRD，贫流股总节点数则为NL×NLG×NLS×NLD。初始状态下，整个结构为空结构，优化开始后随机在富流股和贫流股上抽取两个节点，连接形成质量交换单元。

图3

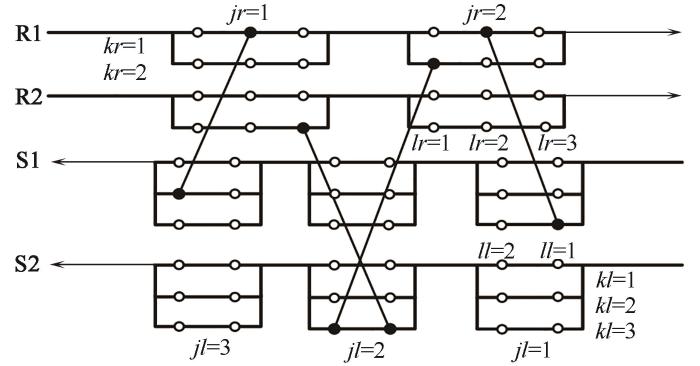
图3 有分流节点非结构模型

Fig.3 Schematic of the nodes-based non-structural model with streams split

1.4 约束条件

(1) 传质可行性约束

$\begin{array}{l} y_{i r, j r, k r, l r}^{i n} > m_{i r, i l} x_{i l, j l, k l, l l}^{o u t} + b_{i r, i l} \\ i r \in N R, j r \in N R G, k r \in N R S, l r \in N R D \\ i l \in N L, j l \in N L G, k l \in N L S, l l \in N L D \end{array}$ (4) $y_{i r, j r, k r, l r}^{o u t} > m_{i r, i l} x_{i l, j l, k l, l l}^{i n} + b_{i r, i l}$ (5)

(2) 传质单元质量守恒

$G_{i r, j r, k r} (y_{i r, j r, k r, l r}^{i n} - y_{i r, j r, k r, l r}^{o u t}) = L_{i l, j l, k l} (x_{i l, j l, k l, l l}^{o u t} - x_{i l, j l, k l, l l}^{i n})$ (6)

(3) 流股质量守恒

$G_{i r} (y_{i r}^{i n} - y_{i r}^{o u t}) = \sum_{i r = 1}^{N R} \sum_{j r = 1}^{N R G} \sum_{k r = 1}^{N R S} \sum_{l r = 1}^{N R D} [G_{i r, j r, k r} (y_{i r, j r, k r, l r}^{i n} - y_{i r, j r, k r, l r}^{o u t}) Z_{i r, j r, k r, l r}]$ (7) $L_{i l} (x_{i l}^{o u t} - x_{i l}^{i n}) = \sum_{i l = 1}^{N L} \sum_{j l = 1}^{N L G} \sum_{k l = 1}^{N L S} \sum_{l l = 1}^{N L D} [L_{i l, j l, k l} (x_{i l, j l, k l, l l}^{o u t} - x_{i l, j l, k l, l l}^{i n}) Z_{i l, j l, k l, l l}]$ (8)

(4) 节点出口浓度约束

$y_{i r, j r, k r, l r}^{i n} \geq y_{i r, j r, k r, l r}^{o u t}$ (9) $x_{i l, j l, k l, l l}^{o u t} \geq x_{i l, j l, k l, l l}^{i n}$ (10)

(5) 流股出口浓度约束

$y_{i r}^{o u t} \leq y_{i r}^{t a r g e t}$ (11) $x_{i l}^{o u t} \leq x_{i l}^{t a r g e t}$ (12)

(6) 流量约束

$\sum_{k r = 1}^{N R S} S P R_{i r, j r, k r} G_{i r, j r, k r} = G_{i r} \leq G_{i r, m a x}$ (13) $\sum_{k l = 1}^{N L S} S P L_{i l, j l, k l} L_{i l, j l, k l} = L_{i l} \leq L_{i l, m a x}$ (14)

2 强制进化随机游走算法

本文基于节点非结构模型，采用RWCE算法[19]同步优化质量交换网络，该算法已在换热网络问题上取得了许多优秀的成果[20-21]，验证了该算法强大的全局搜索能力。RWCE算法的基本原理为：种群中的个体独立进化，每个个体从空结构开始，以目标函数减小为进化方向，通过随机生成传质单元和随机增减传质量、分流比及流量实现整型变量和连续变量的同步进化，同时，有一定的概率接受目标函数较高的结构，具备跳出局部最优解的能力。与以塔板数为优化变量的算法不同，本算法以传质量作为优化变量，并根据质量衡算反求节点的进出口浓度，可避免迭代计算造成的优化效率低下的问题，显著提高优化效率。

2.1 初始化

读取算例的输入参数，设定网络的结构参数，包括富/贫流股的分流组数、分流数、节点数。设置种群规模Np，初始状态下的所有个体均为空结构，并且结构中所有节点对应的变量信息全部归零。

2.2 连续变量游走

需要进行游走操作的变量包括传质量、分流比和贫流股流量。依次对所有节点做循环，若节点上存在传质单元，则该传质单元的连续变量有γ的概率参与游走。当判定要参与游走时，则分流比游走概率为β，传质量游走概率为1-β，流量游走概率为δ。分流比、传质量、贫流股流量分别按照式(15)~式(18)游走。游走公式中1-2r确定随机的游走正负方向，rΔL确定随机的游走步长，此公式保证步长是以0为中心的正态分布，即大概率以小步长搜索，小概率以大步长搜索。

$S P R_{i r, j r, k r}^{'} = S P R_{i r, j r, k r} + (1 - 2 r_{1}) r_{2} Δ L_{S P}$ (15) $S P L_{i l, j l, k l}^{'} = S P L_{i l, j l, k l} + (1 - 2 r_{3}) r_{4} Δ L_{S P}$ (16) $M_{i l, j l, k l, l l}^{'} = M_{i l, j l, k l, l l} + (1 - 2 r_{5}) r_{6} Δ L_{M}$ (17) $L_{i l}^{'} = L_{i l} + (1 - 2 r_{7}) r_{8} Δ L_{L}$ (18)

经过游走后，若一些传质单元的传质量、分流比或流量小于预设的下限Mmin、SPRmin、SPLmin、Lmin，认为这些传质单元已无存在的必要，因此将这种传质单元清除，传质量、分流比、流量以及连接关系全部清零。

2.3 新单元生成

每次迭代有一定概率ε选中任意两个贫富流股的节点，连接形成一个新的传质单元，并赋予此传质单元一个初始的传质量。若该传质单元所在的分流上没有其他传质单元则需要赋予其初始分流比，若该传质单元所在的贫流股上没有其他传质单元，则还需赋予其初始流量，如式(19)~式(22)所示。

$M_{i r, j r, k r, l r}^{_{n e w}} = M_{m a x} r_{9}$ (19) $S P R_{i r, j r, k r}^{n e w} = \{\begin{array}{l} S P R_{m a x} r_{10}, i f S P R_{i r, j r, k r} = 0 \\ S P R_{i r, j r, k r}, e l s e \end{array}$ (20) $S P L_{i l, j l, k l}^{n e w} = \{\begin{array}{l} S P L_{m a x} r_{11}, i f S P L_{i l, j l, k l} = 0 \\ S P L_{i l, j l, k l}, e l s e \end{array}$ (21) $L_{i l}^{n e w} = \{\begin{array}{l} L_{m a x} r_{12}, i f L_{i l} = 0 \\ L_{i l}, e l s e \end{array}$ (22)

2.4 选择与变异

如式(23)所示，当生成阶段结束后，计算费用F1，并与游走前的费用F0进行比较，选择费用较低的结构保留至下一次迭代中。然而，为了防止优化陷入局部最优，即便F1<F0，也仍有一定概率ζ接受费用较差的结构，避免算法早熟。

$S_{i t + 1} = \{\begin{array}{l} S_{i t} i f F_{1} \leq F_{0} \\ S_{i t} e l s e i f r_{13} < ζ \\ S_{i t - 1} e l s e \end{array}$ (23)

式中，向量 Sit 表示第it次迭代的网络结构，包含所有节点的全部变量信息。

3 精细搜索策略的提出

3.1 全局搜索与局部搜索的矛盾

启发式方法是一类具有贪婪性的随机搜索方法，这决定了启发式方法难以兼顾全局搜索和局部搜索。以RWCE算法优化废水脱酚算例为例进行说明，设定两组不同精度的优化参数，对比观察二者所得结果的特点和差异，流股数据和投资费用计算公式见文献[12]。保持模型结构参数相同，设定不同的优化参数，参数A设定较大的步长、进化概率、生成概率以及接受差解概率，而参数B则将以上参数设定为较小值，经过相同次数的迭代后对比两套参数所得的结果。当以参数A进行优化时，在第4.205×108次迭代得到费用为338816 USD·a-1的结果并收敛于此，该结果的结构如图4所示。从图中可知，内部贫流股S1和S2的流量分别为4.9262 kg·s-1和2.2539 kg·s-1，而二者的流量限制分别为5.0000 kg·s-1和3.0000 kg·s-1，由于使用内部贫流股不会带来费用的增加，因此应尽可能多地使用内部贫流股。由此可知，该结构的连续变量仍有优化的空间，但受限于基础算法的固定优化参数，难以得到精度更高的结果，算法往往收敛于非局部最优解。因此，出于保持全局搜索能力的目的而设定的固定参数不利于求解更精确的网络结构，即局部搜索能力不足。

图4

图4 参数A得到的结构

Fig.4 The structure obtained with parameter A

当以参数B进行优化时，如图5所示，得到了一个包含4个传质单元的结构。图6为两套参数优化过程的TAC曲线，可以看出使用参数B时TAC下降频次较少，且下降幅度较小，很快便收敛于368794 USD·a-1，此费用较前者更高。实验结果说明，全程的高精度的优化对全局优化来说是不利的，不仅优化效率降低，而且一旦陷入局部最优解便难以跳出，导致算法的持续优化能力不足。

图5

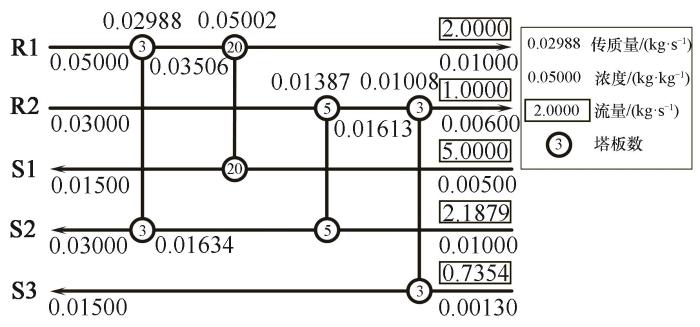
图5 参数B得到的结构

Fig.5 The structure obtained with parameter B

图6

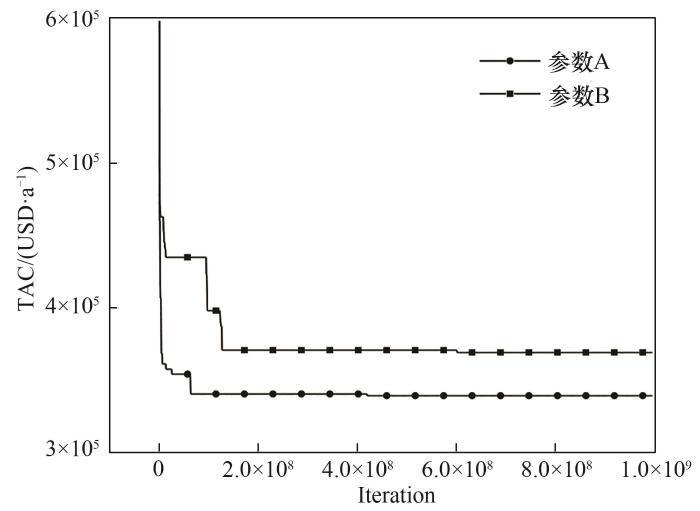
图6 不同优化参数的TAC迭代曲线

Fig.6 TAC iteration curves with different optimization parameters

分析可知，产生以上两个实验现象的原因如下：首先，MINLP问题的局部最优解众多，全局搜索和局部搜索难以兼顾，无论倾向于哪种搜索都会错过一些更好的解；其次，整个优化过程对精度的要求是不同的，优化初期可以搜索到的可行解数量巨大，对算法全局搜索能力的需求更大，而优化后期很难在全局范围内搜索到更好的解，但在局部范围内仍可以搜索到更好的解，因此对算法局部搜索能力的需求更大。鉴于此，可采用前期以较大的步长、进化概率、生成概率，以及接受差解概率进行全局搜索的方式，获得一个初始解，再通过精度更高的方法对该解做进一步的优化，以弥补初始解由于精度不足而未被充分优化的问题。

3.2 精细搜索策略

提出两种应用于质量交换网络优化的精细搜索方法。方法1的核心思想是：将基础RWCE得到的解复制生成大量的新个体，每个新个体均具有相同的初始结构。以该初始结构为中心，在邻域内以更精细化的随机游走进行高精度搜索，并将所得到的更优解作为初始解，再次复制给全部个体进行邻域内的高精度搜索，以此实现更强的局部搜索能力。方法2的核心思想是：借助确定性方法的高精度和快速收敛的特性，对连续变量进行优化。使用坐标轮换法[22]对基础RWCE算法得到的结构进行搜索，该方法将多维的MEN问题转化为一维优化问题，并通过黄金分割法求解极小值点，可降低求解难度，同时也拥有较快的求解速度。

精细搜索是以基础算法获得的结构为起点的局部搜索，而局部搜索能获得更好解的前提是基础算法得到的结构处于较优的解空间内。为了保证基础RWCE算法能获得具有优化潜力的结构，本文通过算法参数的设置来强化初次优化时的全局搜索能力，包括较大的游走步长、传质单元进化概率、生成概率和接受差解概率，保证算法在全局范围内获得一个具有优化潜力的结构，而非收敛于局部最优解，在此基础之上，再进行精细搜索便可得到更优解。两种精细搜索方法步骤如下。

方法1

（1) 初始化阶段：与初始结构设置相同的模型参数，将结构中所有节点的传质量、浓度、分流比和流量全部置零。

(2) 个体分化阶段：读取基础RWCE算法所得最优解的结构数据，并赋值给种群中的所有个体，将该结构的TAC记录为F0。

(3) 迭代阶段：种群中每个个体使用高精度的RWCE算法依次优化，当迭代次数达到ITf,max时，对比种群最优费用Fp与初始费用F0，如果Fp小于F0，则将种群最优个体的结构 Sp记为历史最优结构 SB，否则将初始结构 S0记为历史最优结构，最后将迭代次数归零。

(4) 回代阶段：将历史最优解回代到步骤(2)中，结构数据赋值给种群中的全部个体，作为下一轮迭代的初始结构。

值得注意的是，此方法是基于基础RWCE实现的，保留了RWCE算法的游走、生成、选择与变异等机制，在以局部搜索为主的同时也并未丧失全局搜索能力，因此不仅可以对连续变量做进一步优化，也具有一定的结构变异能力。此外，方法1是基于随机搜索的，收敛速度比较慢，虽然精度较基础算法有所提高，但得到的解仍不是数学意义上的局部最优，因此在对求解速度和精度有较高要求时，该方法存在一定的不足。操作流程如图7所示。

图7

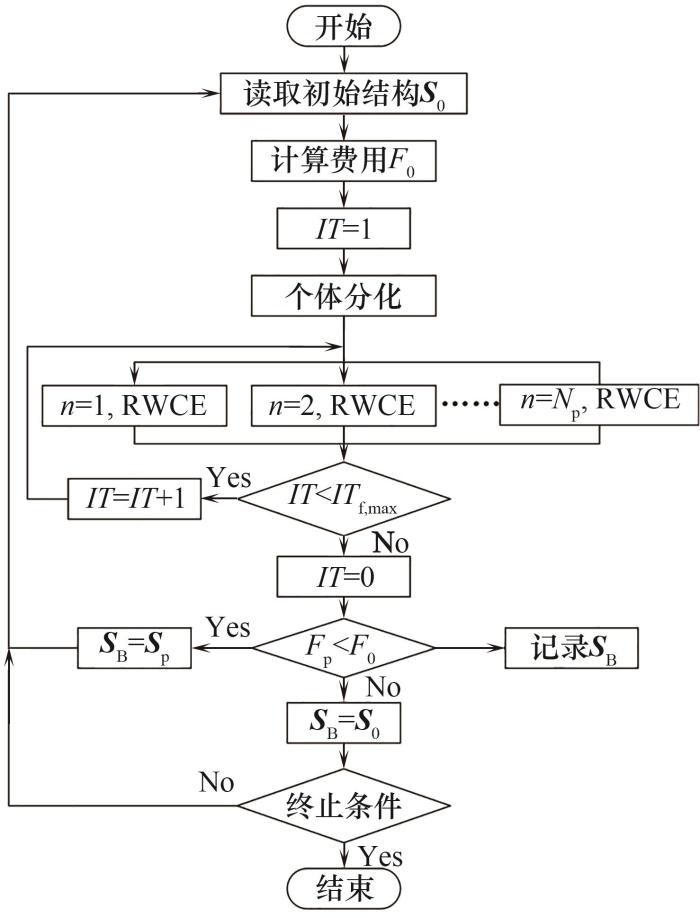
图7 基于启发式算法的精细搜索策略流程

Fig.7 Flow chart of fine search strategy based on heuristic algorithm

方法2

MEN问题包含传质量、分流比、流量三种连续变量，它们共同组成n维向量 x。本方法对优化问题进行降维处理，依次沿着 x 的各个分量方向进行一维搜索，同时保持剩余n-1个分量不变。式(24)~式(26)表示以 xk-1为起点，沿着 ek 分量方向进行一维搜索，求取该方向上的极小值点和最佳步长λB，并将该极小值点作为下一分量的优化起点，对剩下的分量采取相同的操作。当所有分量都优化过一轮之后，再次从第一个分量开始优化，直至某一轮优化前后的目标函数值之差小于η时终止迭代。

$f (x_{k}) = m i n f (x_{k - 1} + λ e_{k})$ (24) $x_{k} = x_{k - 1} + λ_{B} e_{k}$ (25) $e_{k} = (0_{(1)}, 0_{(2)}, \dots, 1_{(k)}, \dots, 0_{(n)})^{T}$ (26)

其中极小值点求取关键在于λ的取值，本文采用的是黄金分割法求取每个分量的最佳步长。在初始搜索区间[a,b]内取两个点α1和α2，其值如式(27)、式(28)所示，计算f (α1)和f (α2)。

$α_{1} = b - 0.618 (b - a)$ (27) $α_{2} = a + 0.618 (b - a)$ (28)

若f (α1)<f (α2)，则舍弃区间(α2,b]，并将区间[a,α2]作为新搜索区间[a1,b1]。若f (α1)>f (α2)，则舍弃区间[a,α1)，并将区间[α1,b]作为新搜索区间[a1,b1]。重复上述步骤，当搜索区间长度缩短至预先设定长度θ时，取区间中点α*作为极小值点，终止迭代，α*与起始点之差即为最佳步长。

基于启发式算法的方法1是一种通用的精细搜索方法，可有效处理不同工况的算例，同时保持了一定的结构变异能力。而处理以填料塔为传质单元的算例时，由于传质单元投资费用是关于传质量的连续函数，因此基于确定性方法的方法2具有较高的精度和较快的收敛速度。但方法2只能对连续变量进行优化，并且只适用于在一个较优解的基础上做小范围的调整，不适用于全局优化。

本文求解环境为Intel(R) Xeon(R) Gold 6226R CPU，主频2.9 GHz，64 GB RAM，采用Fortran90编程。

4 算例验证

4.1 算例1 焦炉气脱硫

本算例取自于文献[3]，流股数据如表1所示，主要目的是去除焦炉气中的硫化氢，以减少燃烧产生的SO2。过程贫流股S1采用稀氨水作为吸收剂，外部贫流股S2采用冷冻甲醇作为吸收剂。传质单元采用筛板塔，投资费用如式(29)~式(34)所示。当相平衡方程为线性时，塔板数的近似计算通常使用Kremser方程求得，但由于方程形式和对数项的存在，计算过程中可能会产生分母为0的情况，这导致了公式的非连续性。因此本文采用Fraser等[23]提出的塔板数公式(30)，通过Underwood近似将Kremser方程转化为连续函数，以此降低计算难度，其中n取1/3，每块塔板的单价为4552 USD·a-1。贫流股总操作费用由单位操作费用乘以流量求得。RWCE算法参数为γ=0.3，β=0.2，δ=0.01，ε=0.002，ζ=0.01，ΔLSP=0.01，ΔLM=3×10-5，ΔLL=0.01，Mmax=0.002，Lmax=0.002，Mmin=10-5，SPRmin=0.01，SPLmin=0.01，Lmin=0.02。

表1 算例1的流股数据

Table 1 Stream data of case 1

流股	最大流量/(kg·s-1)	入口浓度/(kg H2S·kg-1)	目标浓度/(kg H2S·kg-1)	m	b	C0
R1	0.9000	0.07000	0.00030
R2	0.1000	0.05100	0.00010
S1	2.3000	0.00060	0.03100	1.45	0	117360
S2	∞	0.00020	0.00350	0.26	0	176040

新窗口打开| 下载CSV

$C_{1} = \sum_{i r = 1}^{N R} \sum_{j r = 1}^{N R G} \sum_{k r = 1}^{N R S} 4552 N_{i r, j r, k r}$ (29) $N_{i r, j r, k r} = {(\frac{Δ y_{i r, j r, k r}^{n} + Δ y_{i r, j r, k r}^{* n}}{Δ y_{r i g h t, i r, j r, k r}^{n} + Δ y_{l e f t, i r, j r, k r}^{n}})}^{1 / n}$ (30) $Δ y_{i r, j r, k r} = y_{i r, j r, k r}^{i n} - y_{i r, j r, k r}^{o u t}$ (31) $Δ y_{i r, j r, k r}^{*} = (m_{i r, i l} x_{i l, j l, k l}^{o u t} + b_{i r, i l}) - (m_{i r, i l} x_{i l, j l, k l}^{i n} + b_{i r, i l})$ (32) $Δ y_{l e f t, i r, j r, k r} = y_{i r, j r, k r}^{i n} - (m_{i r, i l} x_{i l, j l, k l}^{o u t} + b_{i r, i l})$ (33) $Δ y_{r i g h t, i r, j r, k r} = y_{i r, j r, k r}^{o u t} - (m_{i r, i l} x_{i l, j l, k l}^{i n} + b_{i r, i l})$ (34)

使用基础RWCE优化此算例，花费时长13278 s得到TAC=408996 USD·a-1的结果，包含4个传质单元，总计22块塔板，并且S1流股分为了两股。此结果已低于现有文献中的结果，但仍有继续优化的空间，因此使用精细搜索策略对该结果做进一步优化。采用方法1经过25441 s获得了TAC=407308 USD·a-1的结果，而采用方法2经过24 s获得TAC=407801 USD·a-1的结果，方法1获得了费用更低的结果。方法1的整个优化过程的TAC曲线如图8所示。基础RWCE算法前期使TAC不断下降，随后TAC长期停滞，因此在5.000×108次迭代后使用方法1进行精细搜索，引入精细搜索策略后TAC快速下降，并在接下来的优化过程中多次下降。方法1所得结果相比基础RWCE算法所得结果TAC下降了1688 USD·a-1，相比文献中的最优结果TAC下降了3257 USD·a-1。精细搜索前后的MEN结构如图9所示，相比基础RWCE所得结果，S1的流量下降0.0027 kg·s-1，S2的流量增加了0.0181 kg·s-1，贫流股操作费用上升了2862 USD·a-1，但传质单元R1-S1的塔板数减少了1块，节省了4552 USD·a-1的投资费用，因此使TAC进一步下降。表2将本文结果与文献中的结果进行了对比，得到了目前最优的结果，由此可见，精细搜索策略可以实现对已有结构的深度优化，提升了算法的局部搜索能力。

图8

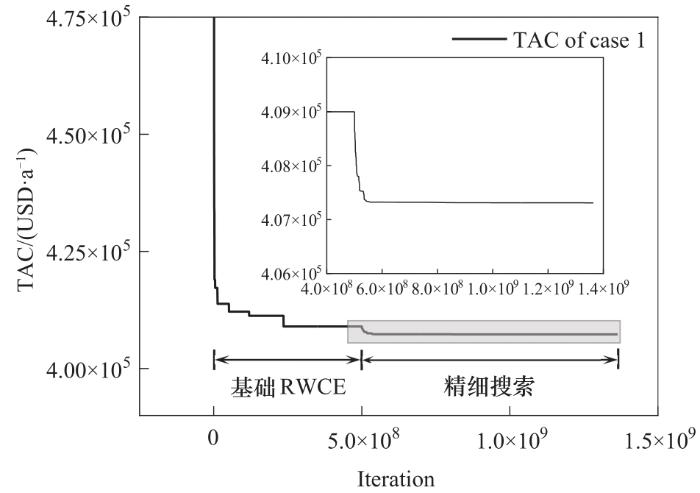
图8 算例1优化全过程的TAC迭代曲线

Fig.8 TAC iterative curve of the whole optimization process of case 1

图9

图9 算例1精细搜索前后的网络结构

Fig.9 Network structure of case 1 before and after fine search

表2 算例1的结果对比

Table 2 Result comparison of case 1

文献	单元数	总塔板数	TAC/(USD·a-1)
[24]	4	—	530471
[25]	5	—	469968
[7]	5	—	431613
[26]	4	25	429700
[27]	4	21	422293
[28]	4	24	420545
[15]	4	20	412500
[16]	4	22	411166
[13]	6	19	410971
[14]	6	19	410565
本文	4	21	407308

新窗口打开| 下载CSV

4.2 算例2 空气除氨

本算例取自于文献[29]，富流股由5股空气组成，主要目的是从空气中去除氨气。S1、S2为过程贫流股，S3为外部贫流股，传质单元采用填料塔，费用计算方法如式(35)~式(37)所示，流股数据如表3所示。

$C_{1} = \sum_{i r = 1}^{N R} \sum_{j r = 1}^{N R G} \sum_{k r = 1}^{N R S} (618 M A S S_{i r, j r, k r}^{0.66} \times 0.225)$ (35) $M A S S_{i r, j r, k r} = \frac{M_{i r, j r, k r}}{0.02 L M C D_{i r, j r, k r}}$ (36) $L M C D_{i r, j r, k r} = \frac{Δ y_{l e f t} - Δ y_{r i g h t}}{l n (Δ y_{l e f t} / Δ y_{r i g h t})}$ (37)

式中，618为单位高度投资费用；MASSir,jr,kr 表示设备质量；0.225为年度化系数，年操作时长为8150 h；0.02为总传质系数；LMCDir,jr,kr 表示对数平均浓度差；Δyleft和Δyright分别表示传质单元左右两端的传质驱动力。RWCE算法参数为γ=0.3，β=0.2，δ=0.1，ε=0.005，ζ=0.001，ΔLSP=0.03，ΔLM=3×10-4，ΔLL=0.1，Mmax=0.002，Lmax=1，Mmin=5×10-5，SPRmin=0.01，SPLmin=0.01，Lmin=0.02。

表3 算例2的流股数据

Table 3 Stream data of case 2

流股	最大流量/(kg·s-1)	入口浓度/(kg NH3·kg-1)	目标浓度/(kg NH3·kg-1)	m	b	C0
R1	2.0000	0.00500	0.00100
R2	4.0000	0.00500	0.00250
R3	3.5000	0.01100	0.00250
R4	1.5000	0.01000	0.00500
R5	0.5000	0.00800	0.00250
S1	1.8000	0.00170	0.00710	1.2	0	0
S2	1.0000	0.00250	0.00850	1	0	0
S3	∞	0.00000	0.01700	0.5	0	0.001

新窗口打开| 下载CSV

高志辉[28]采用自适应模拟退火遗传算法，得到一个包含2次分流、9个传质单元的结构，年综合费用为120717 USD·a-1，但从给出的单元流股信息表中发现，5号单元的富端浓度不符合传质可行性约束，因此结果存在误差。本文采用基础RWCE算法在1.845×108次迭代时得到TAC=129067 USD·a-1的解，用时21977 s，并且直到5.000×108次迭代也未能实现费用下降，因此使用精细搜索策略对该结构进一步优化。采用方法1进行精细搜索时，经过1.751×108次迭代，用时19263 s，获得了128065 USD·a-1的结果。采用方法2进行精细搜索用时51 s，经过1255次迭代，TAC下降至127807 USD·a-1，如图10所示。在本算例中，方法2的速度明显快于方法1，并且费用也有小幅下降，表现出更好的适用性。本文最优结果相比基础程序得到的结果下降了1260 USD·a-1，相比文献[25]中的结果下降了2093 USD·a-1。精细搜索前后的网络结构如图11所示，由于本算例中使用填料塔作为传质单元，因此图中圆圈中的数字表示传质单元的序号而非塔板数。

图10

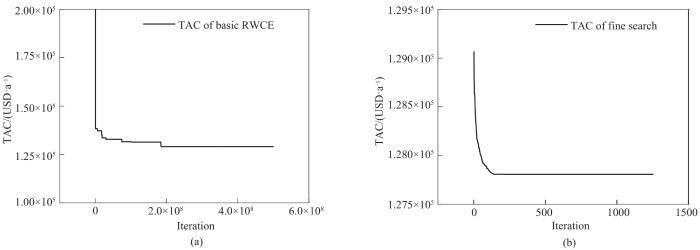
图10 算例2基础RWCE与精细搜索优化过程的TAC曲线

Fig.10 TAC curves of basic RWCE and fine search optimization process of case 2

图11

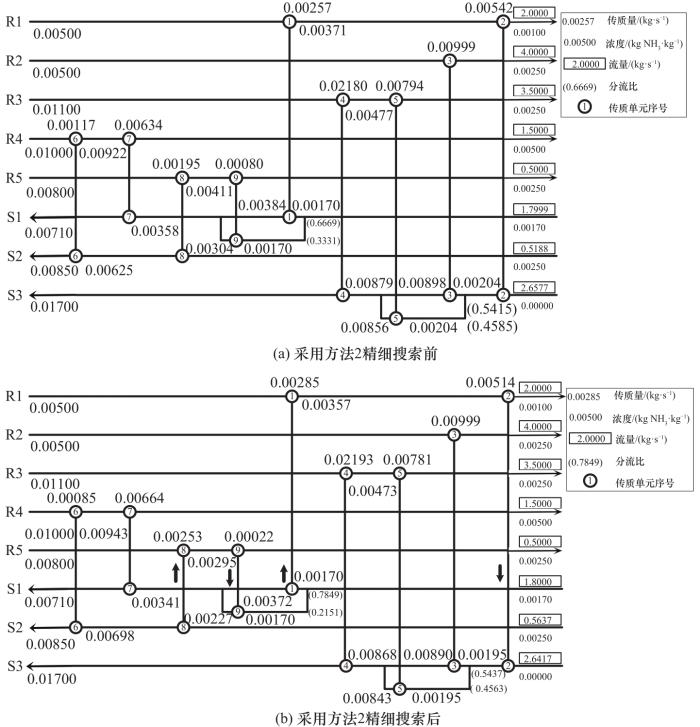
图11 算例2精细搜索前后的结构

Fig.11 Network structure of case 2 before and after fine search

图11两个结构间的差异主要在贫流股S2和S3的流量，以及与之连接的传质单元的传质量。经过精细搜索后，S2的流量增加了0.0449 kg·s-1，与之相连的8号单元传质量增加了0.00058 kg·s-1，与8号单元耦合的9号单元传质量减少了0.00058 kg·s-1，与9号单元在同一组分流的1号单元传质量增加了0.00028 kg·s-1，与1号单元耦合的2号单元减少了0.00028 kg·s-1，这导致了外部贫流股S3承担的传质负荷降低，因此所需流量也降低，使得操作费用降低了469 USD·a-1。此外，精细搜索后传质量有了更好的分配方式，使得结构中设备总投资降低790 USD·a-1。与文献结果的对比列于表4中，验证了基于确定性方法的精细搜索策略对提升算法局部搜索能力的有效性。

表4 算例2的结果对比

Table 4 Result comparison of case 2

文献	单元数	操作费用/(USD·a-1)	投资费用/(USD·a-1)	TAC/(USD·a-1)
[30]	8	85203	48797	134000
[12]	7	82410	50913	133323
[25]	9	81301	48599	129900
[28]	8	73350	47367	120717
本文	9	77508	50299	127807

新窗口打开| 下载CSV

5 结论

（1）低精度的优化参数虽然全局搜索能力较强，但会导致连续变量难以得到充分优化，无法收敛至局部最优解。而高精度的优化参数全局搜索能力较弱，陷入局部最优解陷阱后便难以跳出，导致算法收敛于较差的结果。

（2）提出两种用于对初始解深度优化的精细搜索策略。方法1将最优结构进行不断回代和分化，并以高精度的RWCE算法进行局部搜索，具有适用范围广、优化效果好的优点，且保留了一定的全局搜索能力。方法2采用的坐标轮换法对每个变量的最优解逐个求解，而最优解通过黄金分割法求得，具有速度快、精度高的优点，适合使用填料塔的实例。

（3）将精细搜索策略应用于焦炉气脱硫和空气除氨算例中，分别得到了407308 USD·a-1和127807 USD·a-1的优化结果，与现有文献结果相比经济性提升，验证了该策略的有效性，为费用最小质量交换网络问题提供了一种新的行之有效的优化方法。

符号说明

C0，C1，C2	分别为操作费用系数、投资费用、操作费用，USD·a-1
e	单位向量
F0，F1	分别为游走前后的年综合费用，USD·a-1
IT	迭代次数
L，G	分别为贫、富流股流量，kg·s-1
LMCD	对数平均浓度差，kg·kg-1
ΔL	游走步长
M	传质量，kg
MASS	传质设备质量，kg
m，b	相平衡常数
N	塔板数
NL，NR	分别为贫、富流股的流股数
NLD，NRD	分别为贫、富流股的节点数
NLG，NRG	分别为贫、富流股的分流组数
NLS，NRS	分别为贫、富流股的分流数
Np	种群规模
r	区间(0,1)内的随机数
S	质量交换网络结构
SPL，SPR	分别为贫、富流股的分流比
x	连续变量组成的n维向量
x，y	分别为贫、富流股浓度，kg·kg-1
Z	0/1变量
α	区间边界点
β	分流比进化概率
γ	进化概率
δ	流量进化概率
ε	新单元生成概率
ζ	接受差解概率
η	收敛误差
θ	收敛区间长度
λ	一维搜索步长
上角标
in	流股进口
new	新传质单元
out	流股出口
target	目标浓度
*	平衡浓度
下角标
B	历史最优
il，ir	分别为贫、富流股编号
it	迭代次数
jl，jr	分别为贫、富流股分流组编号
kl，kr	分别为贫、富流股分流编号
L	流量
ll，lr	分别为贫、富流股节点编号
M	传质量
max	上限
min	下限
p	种群最优
SP	分流比

关键字：优秀论文

上一篇：基于知识数据化表达的制冷空调系统故障诊断方法
下一篇：深度融合特征提取网络及其在化工过程软测量中的应用

栏目分类

热门排行

推荐信息

期刊知识