蒸汽在含有不可溶核和可溶无机盐的细颗粒物表面的核化特性

作者：赵庆杰胡晓红张超凡凤仙来源：《化工学报》日期：2022-11-08人气：699

发展生物质发电技术是减少温室气体排放的重要手段之一，对我国推动实现“碳达峰·碳中和”目标具有重要意义。然而，生物质直接燃烧和生物质与煤混合燃烧发电过程排放出大量细颗粒物。这些细颗粒物表面通常含有一定量的可溶无机盐，其中氯化钠（NaCl）、氯化钙（CaCl2）和氯化钾（KCl）占比较多[1]。由于细颗粒物粒径微小，目前工业中应用的常规除尘设备，如静电除尘器、袋式除尘器等对其捕集效果仍较差。鉴于排放到大气中的细颗粒物对人群健康和大气环境带来严重危害，在“双碳”背景下，针对含有可溶无机盐的细颗粒物排放控制技术开展研究非常重要且迫切。对细颗粒物进行预处理，使其粒径增大，以利于常规除尘设备效率的提高，是细颗粒物排放控制的重要技术途径。目前，已发展出声凝并[2]、电凝并[3]和蒸汽凝结[4-6]等颗粒预处理技术。其中，蒸汽凝结预处理技术与烟气湿法、半干法脱酸工艺相结合富有工业应用的潜力，引起了研究者的持续关注[7-9]。

异质核化是蒸汽在颗粒表面凝结的必经过程，由于大气气溶胶颗粒的异质核化对于成云、降水以及雾霾的形成都有着重要影响，异质核化也是大气环境领域关注的重点[10]。现有描述过饱和蒸汽在细颗粒物表面异质核化的理论主要有经典异质核化理论[11]、分子动力学理论[12]、密度函数理论[13]等。其中，经典异质核化理论利用经典热力学方法，基于晶核形成自由能表达式，求解异质核化特性参数，应用该理论研究异质核化具有计算简单、计算量小的特点，在晶核尺度较大或蒸汽饱和度较低时能够获得可靠的预测结果[5,14-15]。鉴于蒸汽凝结颗粒预处理技术中蒸汽饱和度通常在1.1~1.5，经典异质核化理论适用于描述该情况下的异质核化。经典异质核化理论[16]首次提出以来，不断得到发展，主要体现在：将理论推广到含有可溶成分[17-18]、表面粗糙[5]、表面不均匀[19]的颗粒，引入了线张力的影响[20]，考虑了晶核增长机制[21]等。然而，纵观已有理论分析和数值模拟研究，对象集中在不可溶球形颗粒，针对生物质直燃与混燃电站排放的包含可溶无机盐的细颗粒物的研究存在明显不足。尽管Gorbunov等[17]对蒸汽在含有球形不可溶核和NaCl的气溶胶颗粒表面异质核化的晶核形成自由能与平衡蒸汽饱和度进行了数值预测，但由于研究对象为大气环境，研究中采用的蒸汽饱和度接近于1，无法为蒸汽凝结预处理技术脱除细颗粒物的工程应用提供参考。凡凤仙等[22]在接触角为80°条件下对表面含有微量NaCl的细颗粒物的异质核化特性进行了数值预测，采用的蒸汽饱和度为1.8，显得过高；Fan等[18]结合生活垃圾焚烧颗粒的特性，利用数值模拟方法研究了饱和度为1.45条件下，蒸汽在同时含有不可溶球形核和NaCl、CaCl2两种可溶无机盐（二者含量接近）的颗粒表面的异质核化特性，但缺乏对有、无可溶无机盐时成核特性的对比研究，也未对不同成分可溶无机盐的影响进行探究。此外，这些研究在计算成核速率时引入了经验参数成核动能常数，使得计算结果具有不确定性。

针对已有研究存在的问题，本文综合考虑晶核生长的直接沉积机制和表面扩散机制，建立了改进的蒸汽在含有球形不可溶核和可溶无机盐的细颗粒物表面的异质核化模型，基于该模型对蒸汽在不同种类细颗粒物（包括球形不可溶颗粒、表面含有不同可溶无机盐的颗粒）表面异质核化的晶核形成自由能、成核机制和临界饱和度进行对比分析。研究结果对于认识和掌握蒸汽在复杂成分细颗粒物表面的异质核化特性具有重要价值，对于利用蒸汽凝结颗粒预处理技术实现生物质电站细颗粒物的超低排放具有重要意义。

1 模型与算法

1.1 异质核化模型

1.1.1 几何参数的计算

经典异质核化理论认为，蒸汽分子在固体颗粒表面聚集形成球冠形液体晶核，当晶核生长到某一临界尺寸成为临界晶核后，蒸汽依托临界晶核持续凝结，固体颗粒长大为含尘液滴[11, 16]。图1给出了本文所涉及的球形不可溶颗粒、表面含有可溶无机盐的颗粒，以及蒸汽在颗粒表面异质核化形成的球冠形晶核的示意图。图中，点O为球形不可溶颗粒或球形不可溶核的中心，Rp为其半径，O′为气-液界面所在球面的中心，re为晶核半径，s为点O到O′的距离，θ为晶核与颗粒之间的接触角，φ为液-固界面的中心半角，ψ为气-液界面的中心半角。

图1

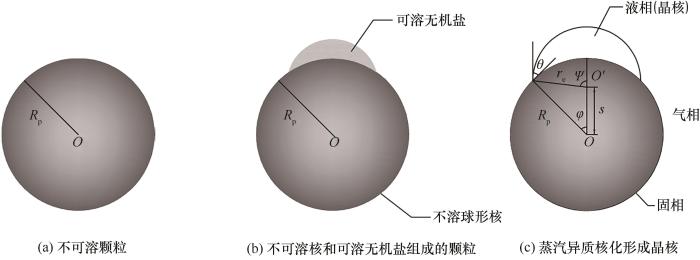
图1 颗粒及蒸汽在颗粒表面异质核化形成晶核示意图

Fig.1 Schematic diagram of particles and embryo formed by heterogeneous nucleation of water vapor on the particle surface

根据图1的几何关系，可得[16]

$L_{g l s} = 2 π r_{e} s i n ψ$ (1) $S_{g l} = 2 π r_{e}^{2} (1 - c o s ψ)$ (2) $S_{l s} = 2 π R_{p}^{2} (1 - c o s φ)$ (3) $V = \frac{1}{3} π r_{e}^{3} (2 - 3 c o s ψ + c o s^{3} ψ) - \frac{1}{3} π R_{p}^{3} (2 - 3 c o s φ + c o s^{3} φ)$ (4)

式中，Lgls为气-液-固三相接触线的周长，m；Sgl 、Sls分别为气-液、液-固界面面积，m2；V为晶核体积，m3；ψ与φ的计算式分别为

$ψ = a r c c o s \frac{R_{p} c o s θ - r_{e}}{s}$ (5) $φ = a r c c o s \frac{R_{p} - r_{e} c o s θ}{s}$ (6)

其中

$s = \sqrt[]{R_{p}^{2} + r_{e}^{2} - 2 R_{p} r_{e} c o s θ}$ (7)

由式(2)~ 式(4)可得[15]

$\frac{d S_{g l}}{d r} = 2 π R_{p} [\frac{2}{X} (1 + \frac{1}{g}) - \frac{c o s θ}{g} + \frac{X - c o s θ}{g^{3}} (1 - X c o s θ)]$ (8) $\frac{d S_{l s}}{d r} = \frac{2 π R_{p} X^{2}}{g} [1 - {(\frac{X - c o s θ}{g})}^{2}]$ (9) $\frac{d V}{d r} = π R_{p}^{2} \{\frac{2}{X^{2}} - \frac{(1 - c o s^{2} θ) X^{2}}{g^{5}} + 2 \frac{1 - X c o s θ}{g X^{2}} +$ $\frac{1 - c o s^{2} θ}{g^{3}} [1 - \frac{(c o s θ - X) (1 - X c o s θ) X}{g^{2}}]\}$ (10)

其中

$X = \frac{R_{p}}{r_{e}}$ (11) $g = \sqrt[]{1 + X^{2} - 2 X c o s θ}$ (12)

1.1.2 晶核形成自由能

蒸汽在不可溶颗粒表面异质核化的晶核形成自由能ΔG可写为[16]

$Δ G = - k T l n S + σ_{g l} S_{g l} + (σ_{l s} - σ_{g s}) S_{l s}$ (13)

式中，k为Boltzmann常数，k = 1.38×10-23 J/K；T为温度，K；S为蒸汽饱和度，S = pv/ps；pv为气相蒸汽压，Pa；ps为温度为T时的饱和蒸气压，Pa；σgl 、σls、σgs分别为气-液、液-固、气-固界面自由能，N/m。

根据Young方程，可得

$σ_{g s} - σ_{l s} = σ_{g l} c o s θ$ (14)

对于包含球形不可溶核和可溶无机盐的颗粒，晶核生长过程伴随着无机盐的溶解。随着晶核中可溶无机盐的摩尔分数的变化，晶核中水的化学势和气-液界面自由能也将发生变化，因而需要采用积分的方法计算晶核形成自由能。恒温、恒压下，晶核形成自由能ΔG与晶核半径re的函数关系可写为[17]

$Δ G (r_{e}) = \int_{0}^{r_{e}} R_{g} T l n (\frac{a_{w}}{S}) \frac{d n_{w}}{d r} d r + \int_{0}^{r_{e}} σ_{g l} \frac{d S_{g l}}{d r} d r + \int_{0}^{r_{e}} (σ_{l s} - σ_{g s}) \frac{d S_{l s}}{d r} d r$ (15)

式中，Rg为通用气体常数，J/(mol·K)；aw为晶核中水的活度；nw为晶核中水的物质的量；r为积分变量，m。

dnw/dr可写为

$\frac{d n_{w}}{d r} = \frac{d V / d r}{d V / d n_{w}}$ (16)

根据晶核质量和密度，其体积V又可写为

$V = \frac{n_{w} M_{w} + n_{s} M_{s}}{ρ_{s}}$ (17)

式中，Mw为水的摩尔质量，kg/mol；ns为晶核中可溶无机盐的物质的量，mol；Ms为可溶无机盐的摩尔质量，kg/mol；ρs为晶核密度，kg/m3。

在晶核生长的起始阶段，晶核为饱和溶液，其密度不随晶核中水的摩尔分数发生变化；随着晶核的生长，晶核转变为不饱和溶液，晶核密度随晶核中水摩尔分数的变化而变化。基于式(17)，当可溶无机盐未完全溶解时

$\frac{d V}{d n_{w}} = \frac{M_{w} (S_{s} + 100)}{100 ρ_{s 0}}$ (18)

式中，Ss为可溶无机盐的溶解度，g/100 g；ρs0为饱和无机盐溶液的密度，kg/m3。

当可溶无机盐完全溶解后

$\frac{d V}{d n_{w}} = [M_{w} ρ_{s} (n_{w}) - (n_{w} M_{w} - n_{w 0} M_{w} + m_{s 0}) \frac{d ρ_{s} (n_{w})}{d n_{w}}] \frac{1}{ρ_{s} (n_{w})}$ (19)

式中，nw0为可溶无机盐刚好完全溶解时晶核中水的物质的量，mol；ms0为可溶无机盐刚好完全溶解时晶核的质量，kg；ρs (nw)表示ρs是nw的函数，即

$ρ_{s} (n_{w}) = \frac{(n_{w} - n_{w 0}) M_{w} + m_{s 0}}{V_{s 0} + (n_{w} - n_{w 0}) M_{w} / ρ_{w}}$ (20)

式中，ρw为水的密度，kg/m3；Vs0为可溶无机盐刚好完全溶解时晶核的体积，m3。

1.1.3 成核速率和临界饱和度

Fletcher经典异质核化理论模型[16]中给出的成核速率的表达式为

$J = 4 π R_{p}^{2} K e x p (- \frac{Δ G^{*}}{k T})$ (21)

式中，J为成核速率，s-1；ΔG*为临界晶核形成自由能，即ΔG的极大值，J；K为成核动力学系数，m-2·s-1。K的值取决于成核条件，具有一定的不确定度，数量级为1028~1031 m-2·s-1，一般取K=1029 m-2·s-1。

为避免采用不确定的成核动力学系数K，依据晶核生长的两种基本机制，即蒸汽分子在晶核表面的沉积机制与水分子在气-液-固三相边界处的表面扩散机制，对K进行计算，从而改进的成核动力学系数K可写为[21]

$K = Z (β_{d e p} + β_{d i f f}) n$ (22)

式中，Z为Zeldovich因子；βdep和βdiff分别为由于直接沉积机制和表面扩散机制引起的水分子添加速率，s-1；n为颗粒表面吸附的水分子的数密度， m-2。

其中

$\begin{matrix} Z = \frac{V_{w}}{π {r_{e}^{*}}^{2}} \sqrt[]{\frac{σ_{g l}}{k T}} \times \\ \sqrt[]{\frac{1}{2 + \frac{(1 - X c o s θ) [2 - 4 X c o s θ - (c o s^{2} θ - 3) X^{2}]}{{(\sqrt[]{1 - 2 X c o s θ + X^{2}})}^{3}}}} \end{matrix}$ (23) $β_{d e p} = \frac{p_{v}}{\sqrt[]{2 π m_{w} k T}} S_{g l}$ (24) $β_{d i f f} = δ υ n e x p (- \frac{Δ G_{d i f f}}{k T}) L_{g l s}$ (25) $n = \frac{p_{v}}{υ \sqrt[]{2 π m_{w} k T}} e x p (\frac{Δ G_{d e s}}{k T})$ (26)

式中，Vw为单个水分子的体积，m3；mw为单个水分子的质量，kg；δ为水分子的平均跳跃距离，m；υ为水分子的振动频率，Hz；ΔGdiff为单个水分子的表面扩散能，J；ΔGdes为单个水分子的沉积能，J。

临界饱和度是指成核速率J = 1 s-1时的蒸汽饱和度，是表征异质核化性能的重要参数之一。经典异质核化理论认为，当蒸汽饱和度达到临界饱和度时，蒸汽将能够以颗粒表面为依托发生显著的核化凝结现象。

1.1.4 活度和气-液界面自由能

对于含有不可溶核和可溶无机盐的颗粒，晶核形成自由能的计算需要建立在无机盐溶液物化性质参数——溶液中水的活度、气-液界面自由能已知的基础之上。晶核中可溶无机盐组分和含量会对气-液、液-固界面自由能带来影响，但不影响气-固界面自由能和接触角。在气-液界面自由能和接触角已知的情况下，基于Young方程可获得气-固、液-固界面自由能之差，使得晶核形成自由能的计算成为可能。

单一组分无机盐溶液中水的活度可写为[23]

$a_{w} = 1 + \sum_{i = 1}^{4} a_{i} (100 x_{i})^{i}$ (27)

式中，xi 为溶液中溶质的质量分数；ai 为常数，由溶质确定。

单一组分无机盐溶液的气-液界面自由能可写为[23]

$σ_{g l} = σ_{w} + B b_{i}$ (28)

式中，σw为水的表面自由能，N/m；bi 为溶液的浓度，mol/kg；B为常数，N·kg/(m·mol)。

气溶胶无机-有机混合物官能团活度系数（aerosol inorganic-organic mixtures functional groups activity coefficient，AIOMFAC）模型[24]和扩展的气溶胶无机物模型（extended aerosol inorganics model，E-AIM）是计算气溶胶系统中溶液物化性质的重要模型[25]，前者给出了活度系数与温度和溶液组分的函数关系，可以计算无机盐溶液中水的活度；后者是气溶胶系统中气体/液体/固体分配的群体模型，可以计算无机盐溶液的气-液界面自由能和有机酸溶液中水的活度。本文利用AIOMFAC模型计算水的活度，利用E-AIM模型计算气-液界面自由能。在此基础上，通过对计算数据分别按照式(27)、式(28)进行曲线拟合，获得可溶无机盐溶液中水的活度和溶液的气-液界面自由能计算式中的系数值。图2给出了常温常压下(T = 298.15 K、p = 101325 Pa)可溶无机盐溶液中水的活度和溶液的气-液界面自由能。图中，离散的点表示模型计算结果，连续的线表示拟合曲线，所得的系数值见表1。

图2

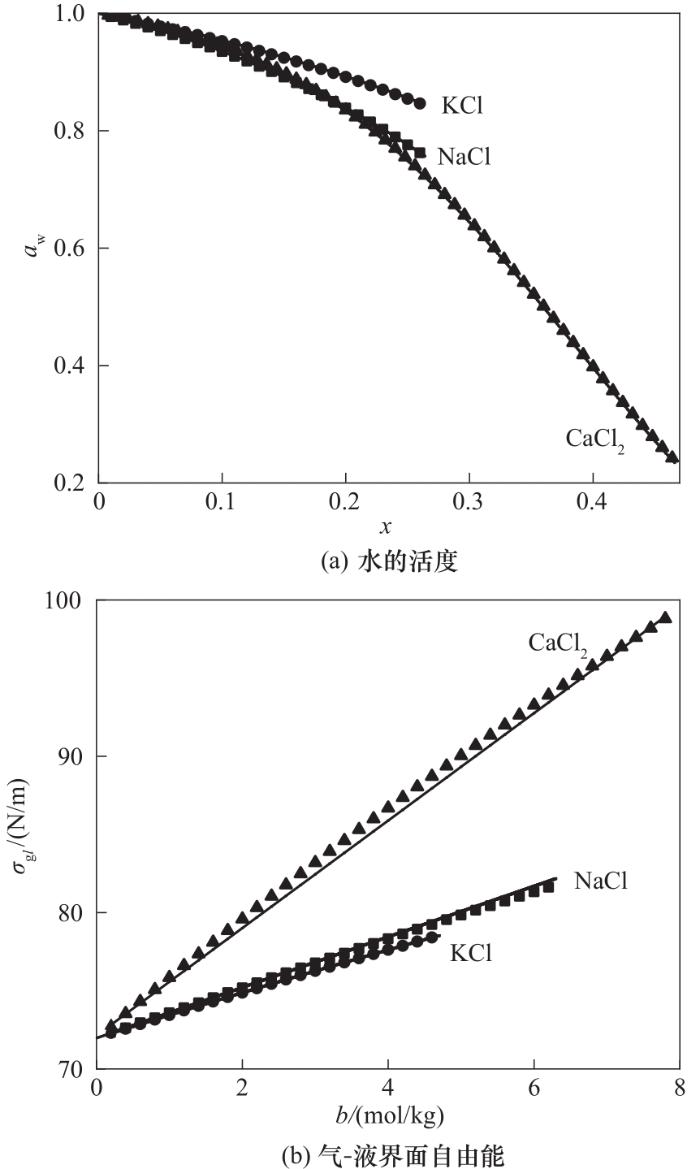
图2 常温常压下无机盐溶液中水的活度和溶液的气-液界面自由能

Fig.2 Water activity and free energy of gas-liquid interface of inorganic salt solution at room temperature and pressure

表1 常温常压下无机盐溶液中水的活度和溶液的气-液界面自由能计算系数

Table 1 Coefficients for calculating water activity and surface tension of inorganic salt solution at room temperature and pressure

参数	符号	NaCl	KCl	CaCl2
活度	a1	-0.5286	-0.3818	-0.5507
	a2	-1.0298	-0.7788	1.3166
	a3	-1.7330	0	-17.9406
	a4	0	0	21.6473
气-液界面自由能	B/(N·kg/(m·mol))	1.6200×10-3	1.4923×10-3	3.4372×10-3

新窗口打开| 下载CSV

1.2 计算方法和计算条件

根据上述理论模型，建立蒸汽在颗粒表面异质核化特性数值模拟平台。在已知颗粒特性和气相温度、压力、蒸汽饱和度条件下，对于不可溶颗粒，可根据式(13)计算任意晶核半径下的晶核形成自由能；对于包含球形不可溶核和可溶无机盐的颗粒，将晶核半径由0以0.01 nm的均匀间隔进行离散，通过数值积分，即可获得晶核形成自由能随晶核半径的变化关系。基于此得到的晶核形成自由能的极大值，即为临界晶核形成自由能，其对应的晶核半径即为临界晶核半径，进而可计算成核速率。成核临界饱和度的计算，采用逐次逼近的方法，具体过程为：(1)将蒸汽饱和度S在1~3以均匀间隔0.01进行离散，生成一系列饱和度值，记为Si = 1+0.01i（i = 0, 1, 2,…, 100）；(2)计算每个Si 条件下的Ji，若|Ji -1|<0.01，则临界成核饱和度Scr=Si；否则，搜寻使得Ji <1、Ji+1>1的饱和度Si 和Si+1，并在两个饱和度之间以均匀间隔(Si+1-Si )/100进行离散，生成一系列饱和度值；(3)重复步骤(2)直至获得成核临界饱和度。数值模拟采用的计算参数见表2，其中水分子特性参数来自文献[26]。此外，受燃料特性和燃烧条件等的影响，生物质燃烧过程排放细颗粒物中可溶无机盐含量存在显著差异；就单个细颗粒物而言，其可溶无机盐质量分数fs可在0~100%之间取值。本文取fs = 20%，事实上，由于对异质核化特性起决定作用的临界晶核尺寸仅为数纳米，颗粒表面上可溶无机盐含量fs ≥ 0.01%时，晶核为饱和溶液，此条件下异质核化特性不受可溶无机盐含量的影响，使得本文结果适用于fs ≥ 0.01%的情况。

表2 数值模拟采用的计算参数

Table 2 Computational parameters used in numerical simulation

参数	符号	单位	数值
温度	T	K	298.15
压力	p	Pa	101325
颗粒中不可溶核的密度	ρp	kg/m3	2400
可溶无机盐质量分数	fs	%	20
单个水分子的质量	mw	kg	2.99×10-26
单个水分子的体积	Vw	m3	2.99×10-29
水分子的平均跳跃距离	δ	m	3.2×10-10
水分子的振动频率	υ	Hz	1×1013
单个水分子的表面扩散能	ΔGdiff	J	2.9×10-21
单个水分子的吸附能	ΔGdes	J	2.9×10-20

新窗口打开| 下载CSV

2 结果与讨论

课题组前期的研究中，将基于经典异质核化理论的蒸汽在不可溶球形颗粒表面的成核临界饱和度数值模拟结果与文献中的实验数据相结合，验证了模型和算法的可靠性[5]。本文将在前期研究的基础上，考察包含不可溶球形核和可溶无机盐的颗粒的核化特性，分析其与球形不可溶颗粒核化特性的差异，以及不同可溶组分对核化特性的影响规律。然而，由于目前尚缺少蒸汽在包含球形不可溶核和可溶无机盐的颗粒表面异质核化特性的实验报道，给相应颗粒异质核化数值模拟结果的实验验证带来困难。尽管最近东南大学张军教授团队[27]借助环境扫描电子显微镜实现了细颗粒物异质核化过程的可视化，但研究对象均为不可溶颗粒。今后的研究中可制备包含球形不可溶核和可溶无机盐的颗粒，并对其核化特性开展实验，为复杂颗粒异质核化理论模型的验证提供数据支持，而本文模拟结果可以为实验研究中参数选择提供先期指导。

2.1 晶核形成自由能

图3给出了S = 1.2、Rp = 0.1 μm条件下得到的无量纲晶核形成自由能ΔG/(kT)随晶核半径re的变化关系。其中，图3(a)~(c)分别为接触角θ = 30°、40°和50°下的结果。由图可见，晶核形成自由能均呈现出随着晶核半径的增加而先增大后减小的趋势，晶核形成自由能的极大值为临界晶核形成自由能，其对应的晶核半径为临界晶核半径。在过饱和蒸汽与细颗粒物组成的系统中，水分子在颗粒表面聚集形成晶核，只有越过临界晶核形成自由能、超过临界晶核半径的晶核才能持续长大，成为液滴。在Rp不变的情况下，随着接触角的增加，临界晶核形成自由能增大，这是因为接触角越大，颗粒的润湿性能越差，越不利于颗粒充当蒸汽相变的凝结核。由图还可见，在接触角一定的情况下，临界晶核形成自由能的大小与颗粒表面是否含有可溶无机盐以及可溶无机盐的种类密切相关。其中，不可溶颗粒的临界晶核形成自由能最大，含CaCl2颗粒的临界晶核形成自由能最小。从物理化学机制上看，晶核形成自由能包括两部分：一是体积项，即水分子由蒸汽态转变为液态，汽液两相化学势的差异，造成系统自由能降低；二是表面项，即液体晶核在颗粒表面生成，气-液和液-固界面取代了原来的气-固界面，使得系统自由能增加。与不可溶颗粒相比，含有可溶无机盐的颗粒表面形成的晶核过程中由于可溶组分的溶解，气液两相化学势之差与气-液界面自由能均增大，从而体积项降低，表面项增加。考虑到体积项与re的立方成正比，表面项与re的平方成正比，随着re的增加，体积项的降低更为显著，使得临界晶核半径与临界晶核形成自由能均更小。此外，由于水的活度通过影响化学势而影响体积项，其对晶核形成自由能的影响更为显著。在模拟条件下，晶核均为饱和溶液，结合图2可知，对于三种可溶无机盐，饱和溶液中水的活度由小到大依次为CaCl2 < NaCl < KCl。综上所述，晶核形成自由能按由小到大的顺序排列为CaCl2 < NaCl < KCl。

图3

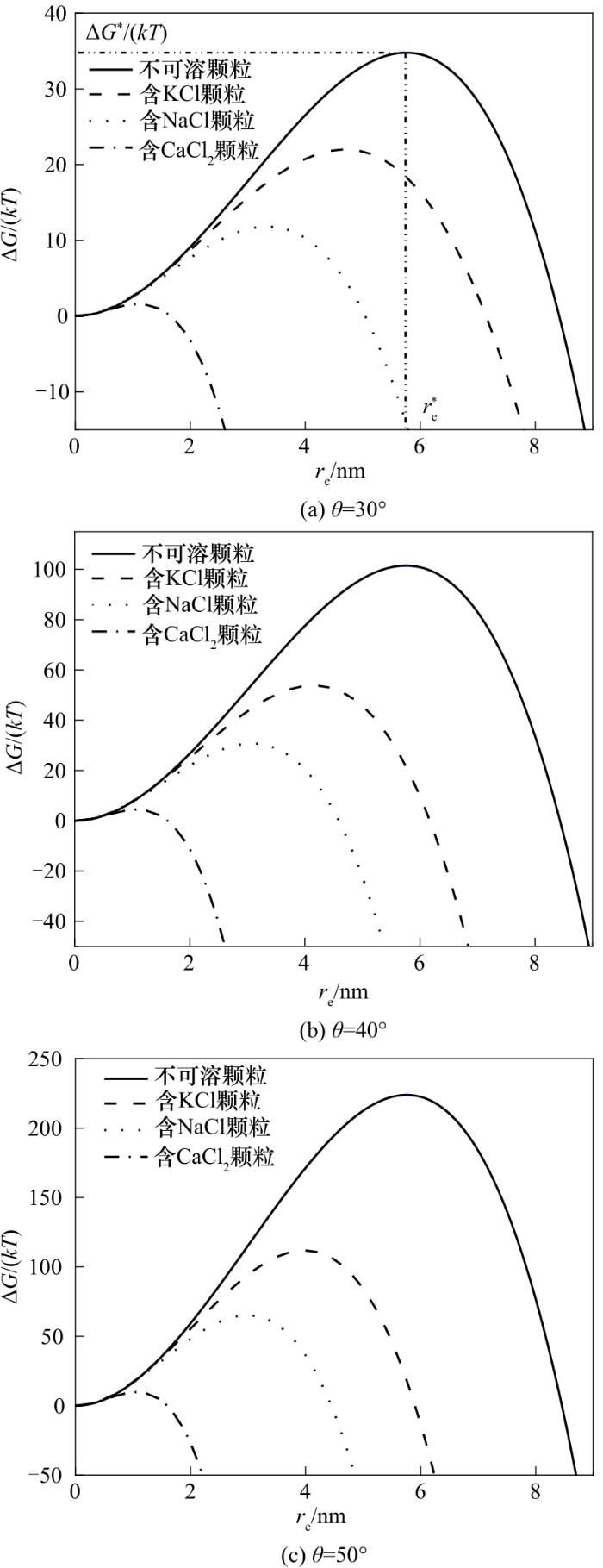
图3 无量纲晶核形成自由能随晶核半径的变化关系

Fig.3 Dimensionless free energy of embryo formation versus embryo radius

晶核生长过程中，可溶无机盐的溶解不仅改变了晶核中水的活度和晶核的气-液界面自由能，还由于溶解度和密度的不同而导致晶核体积随晶核半径的变化规律不同，使得含不同可溶无机盐的颗粒表面上的晶核形成自由能随晶核半径的演变规律不同，从而引起临界晶核形成自由能和临界晶核半径差异显著。图3(a)示出了不可溶颗粒的无量纲临界晶核形成自由能ΔG*/(kT)和临界晶核半径r $e *$ 。当re < r $e *$ 时，由于系统具有自发地由非平衡态向平衡态转变的特性，随着ΔG→0，re→0，晶核将消失；而一旦晶核半径达到r $e *$ ，只要再捕集一个蒸汽分子，即可越过临界晶核形成自由能，之后随着ΔG→0，re单调增大，这表明，颗粒能够充当凝结核，随后颗粒由于持续的凝结增长演变为大粒径的含尘液滴。临界晶核形成自由能和临界晶核半径的存在也表明蒸汽凝结过程中必须经过异质核化过程。一般说来，临界晶核形成自由能和临界晶核半径越小，颗粒的核化性能越好，蒸汽越容易在颗粒表面发生异质核化凝结。因此，四种颗粒相比，不可溶颗粒最难以发生异质核化凝结，含KCl颗粒次之，含NaCl颗粒再次之，含CaCl2颗粒最容易发生异质核化凝结。

2.2 晶核生长机制

欲深入理解晶核生长过程，有必要探讨两种晶核生长机制对晶核生长的贡献。由式(24)、式(25)可知，晶核生长的直接沉积机制和表面扩散机制与晶核的几何参数——气-液界面面积及气-液-固三相接触线的周长密切相关，而晶核的几何参数取决于不可溶颗粒或不可溶核的半径Rp与接触角θ。在S= 1.2条件下开展数值模拟，图4给出了直接沉积和表面扩散机制引起的水分子添加速率之比(βdiff/βdep)的模拟结果。其中，图4(a)为θ = 40°时βdiff/βdep随Rp及晶核半径re的变化情况，图4(b)为θ = 40°时临界晶核半径下βdiff/βdep随Rp的变化情况，图4(c)为Rp = 0.1 μm时临界晶核半径下βdiff/βdep随θ的变化情况。

图4

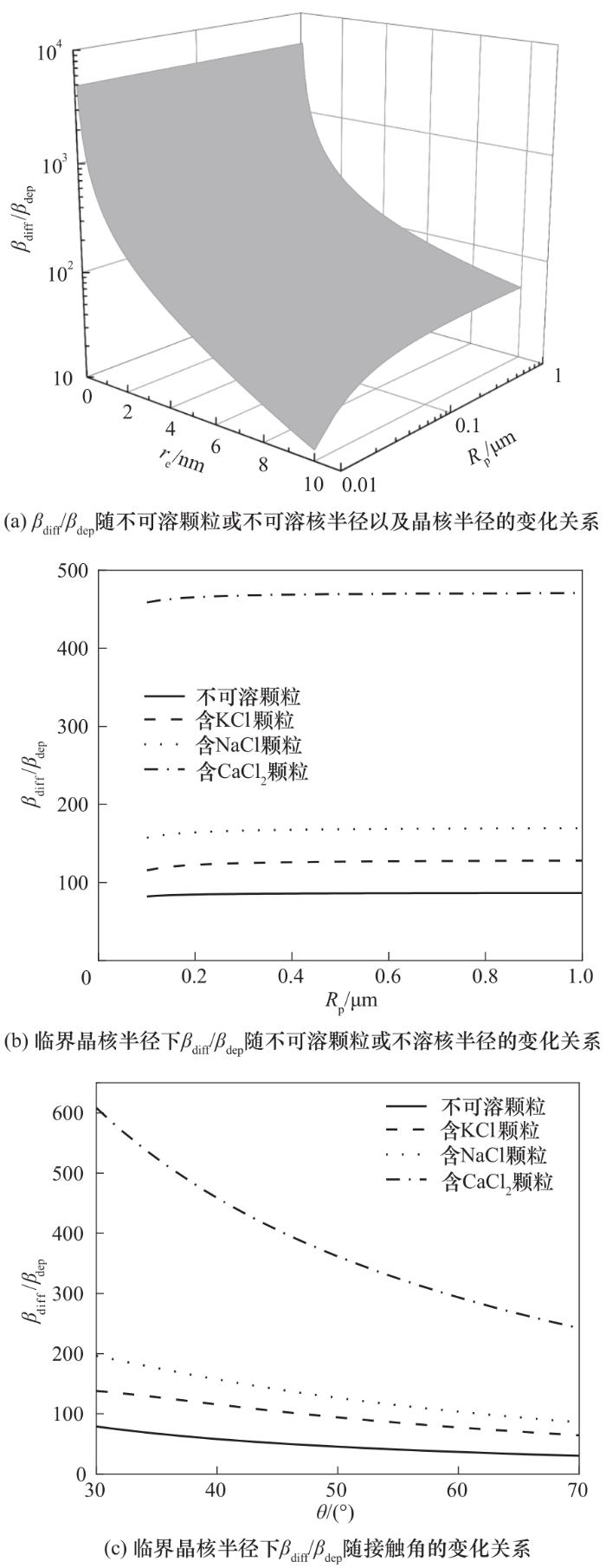
图4 直接沉积和表面扩散机制引起的分子添加速率之比

Fig.4 Ratio of molecule addition rates due to direct deposition and surface diffusion

由图4(a)可以看出，在模拟条件下，表面扩散机制在晶核生长过程中起着决定性作用，对于给定的Rp，随着晶核的增长，蒸汽分子在颗粒表面的直接沉积机制的贡献趋于增大，然而对于re<10 nm的晶核，水分子的表面扩散对晶核生长的贡献仍显著超过蒸汽分子的直接沉积的贡献。此外，由式(24)、式(25)分析可得，两种生长机制引起的分子添加速率均不受颗粒中可溶无机盐的影响，这表明图4(a)中的结果可以表征本文涉及的不可溶球形颗粒和3种包含可溶无机盐和球形不可溶核的颗粒。

然而，颗粒组分的不同会导致临界晶核半径r $e *$ 不同，进而影响到表面扩散和直接沉积两种成核机制对临界晶核增长的贡献。由图4(b)、(c)可以看出，颗粒含有可溶无机盐时，临界晶核半径下βdiff/βdep显著增加，即表面扩散机制对临界晶核生长的贡献更大，特别是含有CaCl2时，βdiff/βdep与不可溶颗粒相比提高了5倍以上。这是因为，当晶核中含有可溶无机盐时，临界晶核半径大幅减小（图3），表面扩散机制引起的分子添加速率βdiff取决于三相接触线的周长，其与晶核半径成正比，表面沉积机制引起的分子添加速率βdep取决于气-液界面面积，其与晶核半径的平方成正比，因此βdiff/βdep与晶核半径成反比，从而临界晶核半径越小，临界晶核半径下βdiff/βdep就越大。临界晶核条件下，对于不同组分颗粒，βdiff/βdep均随Rp呈现出先略有增加，而后保持不变的变化规律，同时βdiff/βdep随θ的增大而单调下降，这同样可以通过临界晶核尺寸的变化加以解释。郭阳等[15]对氨法脱硫系统排放细颗粒物异质核化特性的研究中发现，含有可溶组分(NH4)2SO4与(NH4)HSO4时，临界晶核半径随着不可溶核半径的增大而减小，但减小量迅速下降；而已有异质核化数值模拟研究表明，接触角越大，临界晶核半径越大[5,19]。因此，临界晶核条件下，βdiff/βdep呈现出如图4的变化规律。

2.3 成核临界饱和度

图5给出了成核临界饱和度随不可溶颗粒半径或不可溶核半径以及接触角的变化关系。成核临界饱和度与成核速率密切相关，在成核临界饱和度下，单位时间（1 s）内颗粒表面形成一个临界晶核，即成核速率为1 s-1；并且在气相参数以及Rp相同时，成核速率越高，意味着颗粒异质核化性能更好，颗粒的成核临界饱和度往往更低。图5(a)的数值模拟中保持θ= 40°不变，图5(b)的数值模拟中采用Rp= 0.1 μm。由图5(a)可知，不可溶颗粒与3种含有可溶无机盐的颗粒，成核临界饱和度均随Rp的增大而减小，但成核临界饱和度在数值上差异较大。由图5(a)还可知，在Rp = 0.1 μm条件下，对于不可溶颗粒，Scr = 1.388；对于含有KCl和NaCl的颗粒，Scr分别为1.339、1.209；对于含CaCl2颗粒，Scr = 1.004。这表明不可溶颗粒表面附着有可溶无机盐时，成核临界饱和度下降，特别是附着有CaCl2时，蒸汽只要稍微超过饱和状态，就能够在颗粒表面发生异质核化。由图5(b)可知，接触角对成核临界饱和度有重要影响，接触角越大，成核临界饱和度越大，这是由于接触角大，意味着颗粒润湿性差，水分子更难在颗粒表面聚集，造成颗粒难以充当凝结核，表现为成核速率降低，成核临界饱和度增高，即在更高的饱和度条件，蒸汽才能够在颗粒表面发生异质核化凝结。由图还可以看出，当接触角较小（30°~50°）时，不可溶颗粒的临界饱和度最大；当接触角较大（≥ 50°）时，含KCl和NaCl颗粒的成核临界饱和度逐渐超过不可溶颗粒的成核临界饱和度。例如，当θ = 30°时，不可溶颗粒与含KCl、NaCl、CaCl2颗粒的成核临界饱和度分别为1.218、1.156、1.039、1.002，然而当θ = 70°，4种组分颗粒的成核临界饱和度依次为2.257、2.519、2.315、1.165。含有可溶无机盐的颗粒的成核临界饱和度高于不可溶颗粒的临界饱和度的原因可解释为：接触角增大，引起临界晶核形成自由能和临界晶核半径增大，受可溶无机盐溶解、晶核中水的活度、晶核气-液界面自由能的影响，含可溶无机盐的颗粒与不可溶颗粒之间、含不同可溶无机盐的颗粒之间的临界晶核形成自由能和临界晶核半径的增大程度不同，导致不同种类颗粒的成核速率有不同程度的减小，从而颗粒的成核临界饱和度有不同程度的增加，产生了图5(b)所示的结果。图5中结果还表明，当接触角较大时，除含CaCl2颗粒外，其余3种颗粒的成核临界饱和度均较高，在实际工程应用中，可通过添加润湿剂以降低接触角，改善颗粒的润湿性，从而在较低饱和度条件下实现颗粒的异质核化凝结增长，以降低能耗和水耗。此外，生物质燃烧过程排放细颗粒物有相当一部分是分形团聚体颗粒，已有数值模拟和实验研究均表明，分形结构降低了颗粒接触角，从而有利于颗粒的异质核化，与球形颗粒相比，分形颗粒成核临界饱和度有所下降[18-19]。

图5

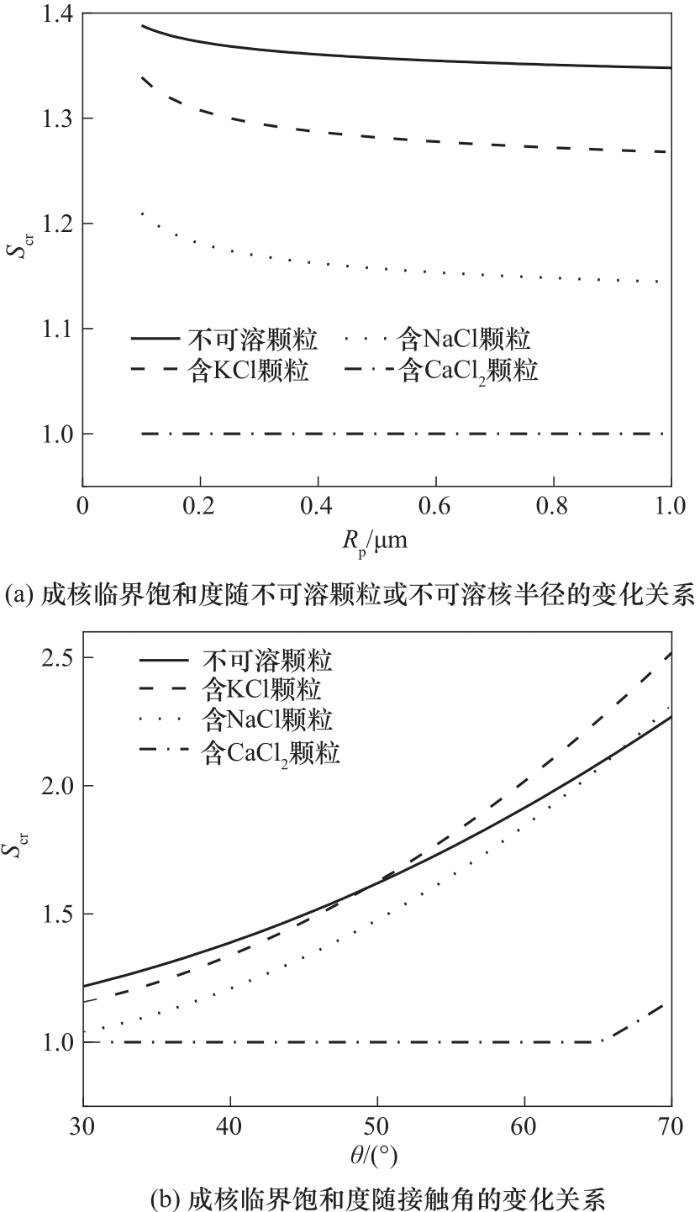
图5 成核临界饱和度

Fig.5 Critical saturation for nucleation

3 结　论

建立了改进的蒸汽在不可溶球形颗粒与包含球形不可溶核和可溶无机盐颗粒表面异质核化模型，利用数值模拟方法，考察了蒸汽在4种细颗粒物（包括不可溶球形颗粒、3种含可溶无机盐的颗粒）表面异质核化的晶核形成自由能、成核机制和临界成核饱和度，得到如下结论。

（1）临界晶核形成自由能和临界晶核半径与颗粒表面是否含有可溶无机盐以及可溶无机盐的种类密切相关，在中等接触角（30°~50°）下，不可溶颗粒的临界晶核形成自由能和临界晶核半径最大，含KCl颗粒次之，含NaCl颗粒再次之，含CaCl2颗粒最小。

（2）表面扩散机制在晶核生长过程中起着决定性作用，随着晶核的增长，蒸汽分子在颗粒表面的直接沉积机制的贡献趋于增大；表面扩散机制与直接沉积机制引起的临界晶核表面上水分子的添加速率之比随颗粒半径的增大先略有增加而后保持不变，随接触角的增大而单调下降；与不可溶颗粒相比，含可溶无机盐的颗粒，表面扩散机制对临界晶核生长的贡献更大。

（3）当接触角较小（30°~50°）时，不可溶颗粒的临界饱和度最大；当接触角较大（≥ 50°）时，含KCl和NaCl颗粒的成核临界饱和度依次超过不可溶颗粒的成核临界饱和度；接触角在30°~70°范围变化时，含CaCl2颗粒的临界成核饱和度始终最小，特别是接触角小于65°时，蒸汽只要稍微超过饱和状态，就能够在颗粒发生异质核化。

符号说明

aw	晶核中水的活度
bi	溶液的浓度，mol/kg
ΔG*	临界晶核形成自由能，J
ΔGdes	单个水分子的吸附能，J
ΔGdiff	单个水分子的表面扩散能，J
J	成核速率，s-1
K	成核动力学系数， m-2·s-1
k	Boltzmann常数，J/K
Lgls	气-液-固三相接触线周长，m
Ms	可溶无机盐的摩尔质量，kg/mol
Mw	水的摩尔质量，kg/mol
ms0	可溶无机盐刚好完全溶解时晶核的质量，kg
mw	单个水分子质量，kg
n	颗粒表面吸附的水分子的数密度，m-2
ns	晶核中可溶无机盐的物质的量，mol
nw	晶核中水的物质的量，mol
nw0	可溶无机盐刚好完全溶解时晶核中水的物质的量，mol
ps	温度为T时的饱和蒸气压，Pa
pv	气相蒸汽压，Pa
Rg	通用气体常数，J/(mol·K)
Rp	不可溶颗粒/不溶核半径，m
re	晶核半径，m
r $e*$	临界晶核半径，m
S	蒸汽饱和度
Sgl	气-液界面面积，m2
Sls	液-固界面面积，m2
Ss	可溶无机盐的溶解度, g/100 g
T	气相温度，K
V	晶核体积，m3
Vs0	可溶无机盐刚好完全溶解时晶核的体积，m3
Vw	单个水分子的体积，m3
xi	溶液中溶质的质量分数
Z	Zeldovich因子
δ	水分子的平均跳跃距离，m
θ	接触角，(°)
υ	水分子振动频率，Hz
ρs	晶核密度，kg/m3
ρs0	饱和无机盐溶液的密度，kg/m3
ρw	水的密度，kg/m3
σgl	气-液界面自由能，N/m
σgs	气-固界面自由能，N/m
σls	液-固界面自由能，N/m
σw	水的表面自由能，N/m
φ	液-固界面的中心半角，（°）
ψ	气-液界面的中心半角，（°）

关键字：优秀论文

上一篇：原位构建富氟SEI的凝胶电解质用于金属锂二次电池
下一篇：界面聚合法制备用于脱氮提纯CH4的N2优先渗透ZIF-90/聚酰胺混合基质膜

栏目分类

热门排行

推荐信息

期刊知识