参考点自适应调整下评价指标驱动的高维多目标进化算法

作者：何江红李军华周日贵来源：《自动化学报》日期：2022-07-23人气：1006

在现实生活中存在大量由多个相互冲突的目标组成的优化问题, 这类问题称为多目标优化问题(Multi-objective optimization problems, MOPs[1]); 超过三个目标的MOPs称为高维多目标优化问题(Many-objective optimization problems, MaOPs[2]), 这类问题广泛存在于实际应用中, 如自动发动机标定问题[3]、水资源分配系统设计[4]、航空发动机健康管理系统[5]、软件重模块化、软件模块聚类问题[6]等.

研究证明传统的多目标进化算法(Multi-objective evolutionary algorithms, MOEAs)在处理MOPs时能获得较好的性能, 然而在处理MaOPs时却会出现一系列的问题[7], 如: 随着目标数目的增加, 种群中非支配解比例呈指数形式增加, 算法的选择压力缺失; 在高维空间中, 部分性能评价指标(如超体积指标)的计算代价过大等. 为了应对目标数目增加带来的挑战, 提高MOEAs在处理MaOPs时的能力, 研究学者们提出一系列算法, 大致可以分为3类, 分别为: 基于松弛支配的算法、基于分解的算法、基于指标的算法.

1)基于松弛支配的算法: 通过修改支配关系扩大解的支配区域, 能在一定程度上缓解支配受阻现象; 常见的松弛支配关系有: 角度支配[8]、网格支配[9]、模糊支配[10]、基于参考点的支配[11]等.

2)基于分解的算法: 利用一组参考向量将一个MOPs分解为多个单目标优化问题(Single-objective optimization problems, SOPs)或更为简单的MOPs, 随后对这些子问题进行协同进化, 这在一定程度上增加了种群的多样性; 此类经典算法有: MOEA/D[12]、MOEA/D-ANA[13]、RVEA[14]、MOEA/D-ROD[15]、NGSA-III[16]、MOEA-PPF[17].

3)基于指标的算法: 通过构建适应度函数将候选解的目标值映射到一个确定的数值上, 并将该值作为环境选择中的选择标准, 该方法能够区分具有相同目标和的解; 此类经典算法有: SMS-EMOA[18]、MOMBI-II[19]、MaOEA-IPB[20]、R2-OSP[21]、MaOEA/IGD[22]等.

尽管上述算法能在一定程度上缓解传统算法在处理高维优化问题时存在的不足, 但面对具有不规则Pareto前沿(Pareto front, PF)的优化问题时, 常规方法可能无法获得很好的性能, 因此需要设计更先进的算法. 目前处理不规则优化问题的算法可以分为四类, 分别是采用固定参考向量与辅助选择方法协同合作, 在搜索过程中根据种群分布调整参考向量, 用参考点同时衡量多样性和保持收敛性, 以及对群体进行聚类或划分目标空间为子区域[23].其中参考向量的调整是非常重要的, Ma等在文献[24]中对单纯性上的各种参考向量调整策略进行综述, 将其分为随机调整、基于拟合的调整、局部种群指导的调整、局部档案的调整、基于邻域参考向量的调整和基于偏好的调整, 并且详细讨论了每种方法的优缺点以及有待解决的问题. 除此之外, 近年来研究学者还结合不同的策略提出一些新型算法, 如 Yuan等在文献[25]中提出PREA, 该算法基于平行距离进行个体选择, 与传统的角度距离、径向交叉距离相比, 基于平行距离导出的点无论是在凹型、凸型, 还是在不规则PF上都是均匀分布的, 这有利于提高算法在处理各种优化问题时的多样性; Liu提出FDEA[26], 该算法利用模糊预测评估不同形状PF上解的相似性, 并以此为依据对种群进行分割, 有效地提高了算法的多样性, 同时提供一个共享权重向量加快收敛速度, 两者共同作用提高算法的性能.

为了能够更好地处理不规则MaOPs, 提高算法的通用性, 本文提出参考点自适应调整下评价指标驱动的高维多目标进化算法, 该算法的具体步骤如下: 1)为了有效地生成一组参考点, 提出一个PF形状监测基础上的自适应参考点策略, 该方法首先利用一条特定的轮廓曲线近似PF, 其次在该曲线上找到所有非支配解对应的点, 然后以对应点之间的距离作为多样性选择标准, 最后利用该准则选择一组多样性好的解作为参考点, 此外基于曲线参数对参考点的位置进行调整, 以减少偏离种群的参考点所产生的影响; 2)为了进一步提高算法性能, 在匹配选择中结合Pareto支配和改进的Pareto支配以及邻域关系, 选择一组有希望的解作为父代种群; 3)为了最终生成一组接近PF且分布广泛的种群, 在环境选择中利用参考点计算基于指标的适应度函数, 将其作为选择标准进行精英选择.

1. 基础知识和相关工作

1.1 基础知识

一个具有n个决策变量和m个目标变量的最小化MOPs可以表示为:

(1)

其中x = (x1, ···, xn)T ∈ X 是n维决策向量, X表示n维决策空间; y = (y1, ···, ym)T ∈ Y 是m维目标向量, Y是m维目标空间; f : X→Y构成m个相互冲突的目标函数, 是一个从n维决策空间X到m维目标空间Y的映射. 在决策空间中, 若解x Pareto支配解y ( $x ≺ y$ ), 则需满足:

(2)

其中fi(x)为解x在第i个目标上的真实目标值.

若在决策空间中不存在x使得 $x ≺ x^{*}$ , 则x*为Pareto最优解, F(x*)为Pareto最优向量; 由于MOPs目标之间相互冲突的性质, 一个目标性能的提升通常会导致其他目标性能的下降, 因此需要一组Pareto最优解作为不同目标之间的权衡, 这样的一组解被称为Pareto解集(Pareto set, PS), 对应的在目标空间中的Pareto最优向量集被称为PF.

1.2 自适应参考点策略

在一些进化算法中通常需要一组在PF上均匀采样的参考点用于指标值的计算, 或一组均匀分布的参考向量用于划分子种群, 本文统一采用参考点代替参考向量以及权重向量. 由于在大部分的优化问题中, 真实PF是不可知的, 因此需要不断地对参考点进行调整使其尽可能地近似PF; 为了达到这个目的, 研究学者们提出了一系列自适应参考点策略.

在RVEA中, 根据当前种群中目标值的范围调整参考向量, 实现目标函数在没有被标准化到相同范围的情况下, 依然能得到一组均匀分布的参考点; NSGA-III中提出基于候选解的分布位置增加和删除参考点; MOEA/D引入档案对参考点进行管理, 若候选解位于稀疏区域, 则将其选入档案并生成相应的参考点.

然而上述所提到的自适应参考点策略存在局限性, 例如在一些优化问题中频繁地更新参考点在一定程度上影响种群的收敛性, 导致出现局部收敛现象; 一些自适应参考点策略的有效性取决于用户预先定义参数; 某些自适应方法对不同PF的优化问题普适性低等. 因此本文提出一个新的自适应参考点策略, 该策略基于PF形状设计多样性评估准则, 并根据该准则选择一组分布广泛的非支配解作为参考点, 另外利用曲线参数调整参考点的位置, 最终生成一组近似PF的参考点用于指标值的计算.

1.3 IGD-NS指标

研究学者提出许多性能指标, 如世代距离(Generational distance, GD[27])、反世代距离(Inverted generational distance, IGD[28])、超体积(Hypervolume, HV[29-31])、R2[32-33]、纯多样性(Pure diversity, PD[34])、增强的反世代距离指标(Enhanced inverted generational distance, IGD-NS[35-36])等, 这些指标被广泛用于评估种群的收敛性、多样性, 或同时评估收敛性和多样性, 下面具体介绍现存的性能指标:

1) GD指标

(3)

其中P为非支配解集, P* 为从PF上均匀采样的参考点; GD指标计算非支配解与参考点之间的最小欧氏距离的平均值, GD值越小表明种群的收敛性越好; 但该指标无法评估种群的多样性, 若所有的非支配解重合在同一个点, 且该点与参考点之间的欧氏距离很小, 则依然能得到一个较好的GD值, 然而此时种群不具有多样性.

2) IGD指标

(4)

其中P为非支配解集, P* 为从PF上均匀采样的参考点; IGD指标与GD指标相似, 计算每个参考点与非支配解之间的最小欧氏距离的平均值, IGD值越小, 种群质量越好; 该指标利用欧氏距离评估收敛性, 利用参考点的均匀分布保证多样性, 因此能够同时评估种群的收敛性和多样性.

3) HV指标

(5)

(6)

其中P为解集, q为目标空间中的预定义参考点, 1H(P, q)为H(P, q)的特征函数; HV指标计算种群到参考点所覆盖的面积, HV值越大种群质量越好; 相比于GD指标和IGD指标, HV的计算不需要PF的先验信息, 然而随着目标数目的增加, 计算复杂度成指数形式增加.

4) R2指标

(7)

其中P为种群, V为参考向量集, z*为当前理想点; R2指标将候选解从目标空间映射到效用空间以计算种群的质量, R2指标值越小说明种群质量越好; 然而R2指标对中间区域存在固有的偏好, 尤其在凸型PF的优化问题上, 分布在中间区域的种群能得到一个较低的R2指标值.

近年来, IGD-NS指标受到研究学者们的广泛关注, 该指标是 Tian等在MOEA/IGD-NS[35]中首次提出的, 与IGD指标相比, 该指标可以区分对种群没有贡献的解. 文献[35]中对无贡献解做了严格定义, 即在计算指标值时由于不是任何参考点的最近邻域而被忽略, 从而对种群的指标值不产生贡献的解. 无贡献解 $y^{'}$ 公式定义为:

(8)

根据无贡献解的定义, 可以得到IGD-NS指标的定义:

(9)

其中P* 为一组均匀分布的参考点, P为非支配解集, P' 为无贡献解集; 由公式可知前半部分与IGD指标的计算方法一致, 后半部分为无贡献解到参考点的距离, 只有同时满足与参考点之间的距离小和无贡献解的数量少两个条件才能得到一个较好的指标值.

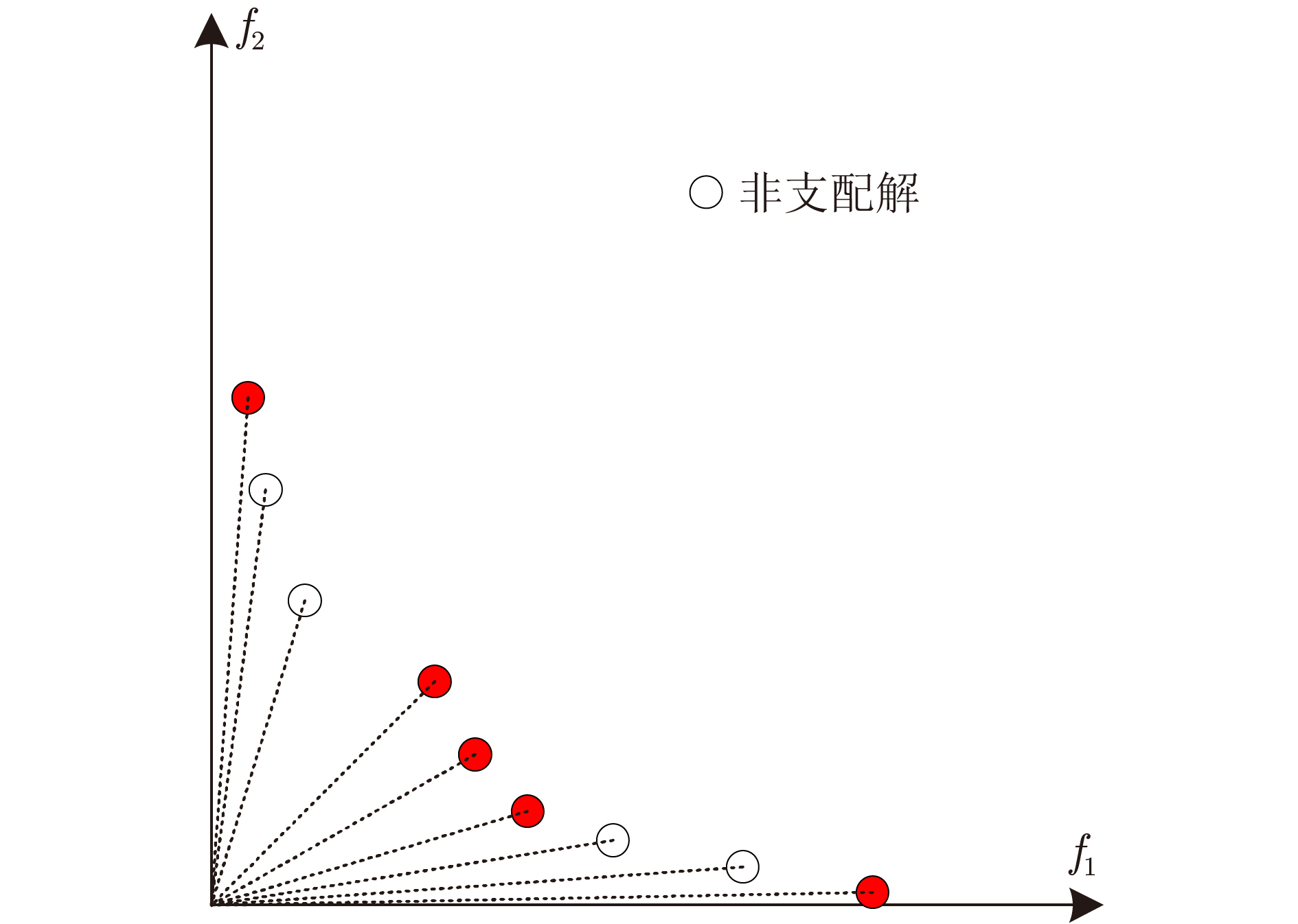
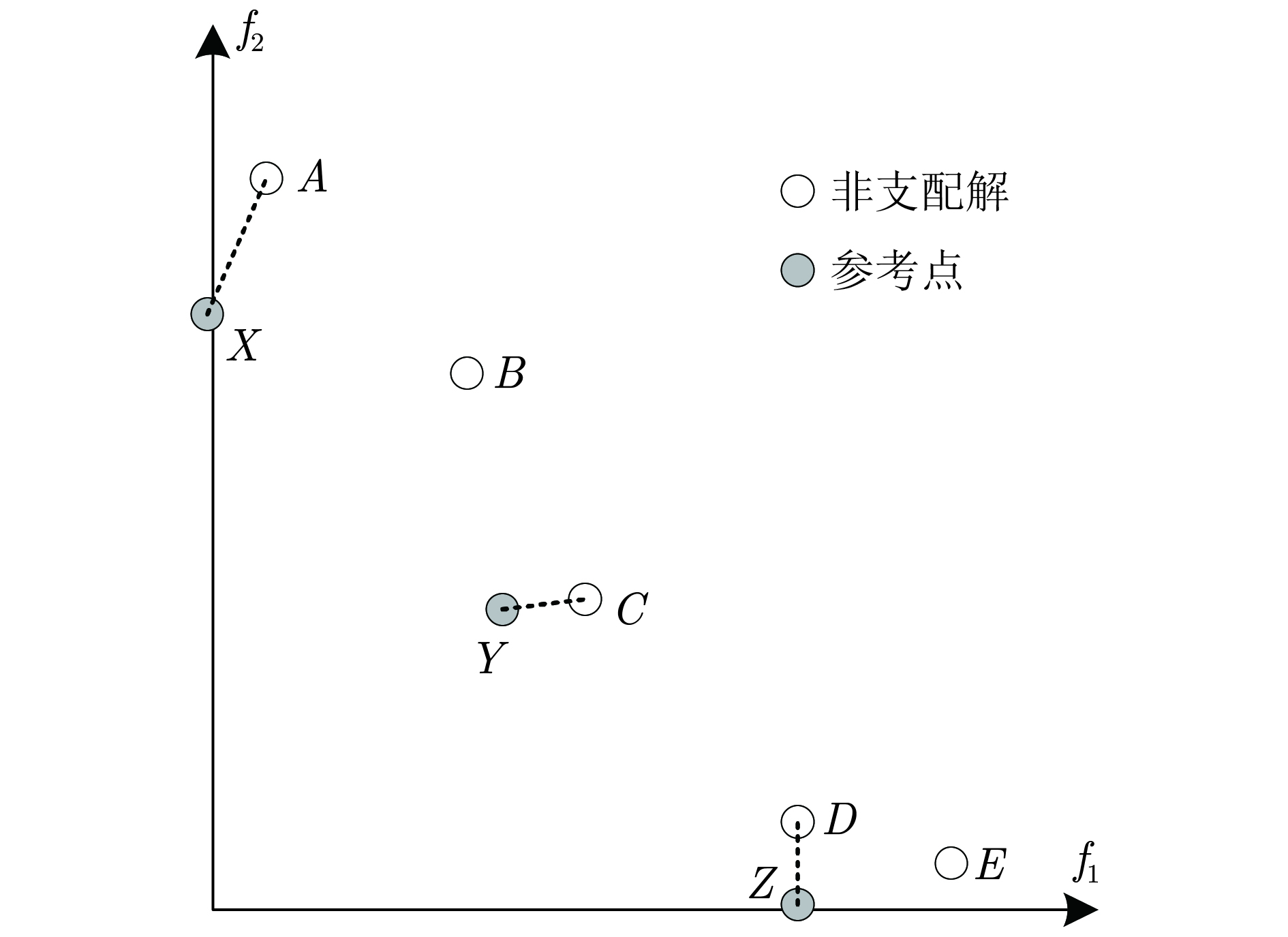
Tian等[35]不但对无贡献解进行公式定义, 为了便于理解, 还佐以图例解释. 如图1所示, X、Y、Z为参考点, A、B、C、D、E为非支配解, 根据上述无贡献解的定义, B、E不属于任意一个参考点的最近邻域, 为无贡献解. 若在环境选择中选取4个解作为下一代种群, 则需要从当前非支配解集中删除1个候选解, 如果使用IGD指标评估种群的质量, {A、D、C}, {A、B、C、D、E}, {A、D、C、B}, {A、D、C、E} 4个解集的IGD指标值相同, 无法区分最差解; 而IGD-NS指标由于能够区分B、E两个无贡献解, 因此能更准确地评估种群的质量.

图 1 二目标下的无贡献解

Fig. 1 The noncontributed solutions under bi-objective

根据以上分析, IGD-NS指标与GD指标相比, 可以同时评估种群收敛性和多样性; 与IGD指标相比, 可以区分无贡献解; 与HV指标相比, 在高维空间中计算代价小; 与R2指标相比, 对边界解或中心解不存在偏好. 基于这些性质, IGD-NS指标适合作为选择标准用于进化算法中.

2. 参考点自适应调整下评价指标驱动的高维多目标进化算法

2.1 算法基本框架

算法1为MaOEA-IAR的主要框架, 首先输入种群规模以及最大进化代数, 随机生成一个规模为N的初始种群P0; 其次在主循环中, 通过匹配选择生成父代种群, 进而生成子代种群, 子代种群和初始种群合并, 最后对合并种群进行环境选择生成下一代种群. 下面将着重介绍算法的4个子部分, 分别为匹配选择、环境选择、自适应参考点和确定轮廓曲线.

算法1. MaOEA-IAR算法框架

输入: N (种群规模); tmax (最大进化代数);

输出: $P_{t_{m a x}}$ (最终种群);

1) P0 = Initialization(N);

2) while t < tmax do

3) 　Qt = MatingSelection(Pt);　　/*匹配选择*/

4) 　Qt' = Variation(Qt, N);

5) 　Pt = Pt ∪ Qt';

6) 　Pt+1 = EnvironmentalSelection(Pt); /*环境选择*/

7) 　t = t+1;

8) end while

2.2 匹配选择

匹配选择能够从当前种群中选择一组有希望的解作为父代种群加入交配池. 在传统的算法中, 通常会利用Pareto支配关系选择父代种群; 然而在高维空间中个体之间互不支配, 难以选择非支配解; 因此本文采用改进的Pareto支配, 将目标值的比较替换成子空间位置的比较, 对个体进行定量比较能够增加选择压力, 具体过程如算法 $2$ 所示.

首先将目标空间划分为多个子空间, 并计算个体所处子空间的位置yindex, 计算方法为:

(10)

(11)

其中yi为个体y在第i个目标上的目标值, Ti为第i个目标的邻域范围, z为理想点, z*为最低点; 并且假设将整个目标空间分为rm个子空间, 即将每个目标均分为r等分, 将个体所在的子空间作为其所在的邻域, 邻域范围即为T.

其次从种群中随机选取2个个体, 通过Pareto支配以及改进的Pareto支配选择非支配解加入交配池中, 在改进的Pareto支配中, 若x支配y, 则需要满足:

(12)

其中 $x_{i n d e x_{i}}$ 为个体x在第i个目标上的位置, $y_{i n d e x_{i}}$ 为个体y在第i个目标上的位置.

算法2. 匹配选择

输入: Pt (种群);

输出: Qt (子代种群);

1) 划分目标空间并计算所有个体所处子空间的位置

2) if |Qt| < N

3) 　/*随机从种群Pt中选择两个个体p, q*/

4) 　if $p ≺ q$ then

5) 　　Qt = Qt ∪ {p};

6) 　else if $q ≺ p$

7) 　　Qt = Qt ∪ {q};

8) 　else if NUM(p) < NUM(q)

9) 　　Qt = Qt ∪ {p};

10)　else if NUM(p) > NUM(q)

11)　　Qt = Qt ∪ {q};

12)　else

13)　　Qt = Qt ∪ {p/q};

14)　end if

15) end if

然后在无法判断支配关系的情况下, 计算个体所处邻域内解的个数NUM, 选择多样性好的个体加入交配池; 最后若多样性也相近, 则随机选取1个个体加入交配池中.

2.3 环境选择

环境选择的目的是从合并种群中获得一组接近PF且分布良好的解集. 算法3给出了环境选择的基本步骤: 首先对种群中的个体进行非支配排序, 选择前k−1个等级中的个体作为下一代, 再将第k个等级中的个体通过适应度值进行删除操作, 直到下一代种群中的个体数与初始种群相等(k值由每个等级中的个体数确定, 为满足 $| ⋃_{i = 1}^{k} F r o n t_{i} | \geq N$ 的最小值, 即 $| ⋃_{i = 1}^{k - 1} F r o n t_{i} | < N$ , 其中N为初始种群中的个体数). 当目标数较小时, 能够通过非支配排序选择出部分解, 再通过适应度值选择剩下的解; 当目标数增大时, 种群中几乎所有的解都为非支配解, 此时算法主要通过基于IGD-NS指标的适应度值选择下一代种群, 非支配解p的适应度为:

(13)

其中P* 为一组多样性好的参考点.

算法3. 环境选择

输入: Pt (合并种群);

输出: Pt+1 (下一代种群);

1) (F1, F2, ···, Fi) ← NondominatedSort(Pt);

2) k ← minimum number satisfies $| ⋃_{i = 1}^{k} F_{i} | \geq N$ ;

3) $P_{t + 1} \leftarrow ⋃_{i = 1}^{k - 1} F_{i}$ ;

4) P* = GenerateReferencePoint(Fk); /*生成参考点*/

5) while |Fk| ≥ N − |Q| do

6) 　 $p \leftarrow \arg min_{p \in F_{k}} F i t n e s s_{p}$ ;

7) 　Fk ← Fk\{p};

8) end while

9) Pt+1 ← Pt+1 ∪ Fk;

10) return Pt+1;

2.4 PF形状监测基础上的自适应参考点策略

传统基于角度距离的多样性评估准则在处理非线性 $P F$ 优化问题时存在偏差, 尤其在凹型PF中, 相同大小的角度距离不能生成均匀分布的候选解, 如图2所示, 被选择的候选解倾向于分布在中心区域. 因此在生成参考点的过程中, 利用基于PF形状的多样性评估准则对参考点进行自适应, 这在一定程度上可以减少这种偏差; 由于单独使用多样性评估准则选择参考点可能生成偏离种群的参考点, 利用理想点或最低点对参考点的位置进行调整, 能够降低此类参考点的影响.

图 2 基于角度距离选择参考点

Fig. 2 Select reference points based on angular distance

算法4. 生成参考点

输入: P (非支配解集); N (参考点规模); r (邻域参数);

输出: P* (参考点集);

1) Q = $\emptyset$ ;

2) /*通过算法5找到合适的轮廓曲线并确定曲线参数p以及所有候选解的对应点*/

3) p = Shape_Estimate(P);

4) /*选择m个边界解作为参照点并且放入Q中*/

5) while Q < N

6) /*计算种群中剩余非支配解x与Q中的参照点y之间的差异D*/

7) 　Q = Q ∪ max(D(x, y));

8) end while

9) for each y∈Q do

10) 　if p = 1

11) 　　P* = Q;

12) 　else if p > 1

13) 　　P* = P* ∪ {y**};

14) 　else

15) 　　P* = P* ∪ {y*};

16) 　end if

17) end for

18) if $| P^{*} |$ < N then

19) 　r++;

20) 　/*将目标空间重新划分生成新的参考点*/

21) end if

算法4为自适应参考点的具体步骤, 首先根据当前种群状态, 用一条特定的轮廓曲线近似PF并得到曲线参数p; 然后在该曲线上找到所有非支配解的对应点, 基于对应点设置多样性评估准则; 之后将边界解添加到参照点集合Q, 以该准则计算剩余非支配解与参照点之间的差异, 选择差异最大的非支配解加入集合Q中, 直到集合内个体的数量满足N, 将Q中的所有个体作为初始参考点, 差异值的计算公式如下:

(14)

其中x为剩余非支配解, y为参照点; x＇、y＇分别为x、y在曲线上的对应点; fi(x＇)、fi(y＇)分别为x＇、y＇在第i个目标上的值.

最后由于只考虑了多样性方面的差异, 可能生成部分偏离种群的参考点, 为了降低此类参考点的影响, 在凸型PF问题中, 将初始参考点调整为所在邻域内的理想点, 在凹型PF问题中, 将初始参考点调整为所在邻域内的最低点. 调整之后的参考点如下:

(15)

(16)

其中y*为凸型PF中调整之后的参考点, y**为凹型PF中调整之后的参考点, y为初始参考点, z为理想点, z*为最低点, r为邻域参数, T为邻域范围.

此外, 由于邻域参数r是用户预先定义的参数, 在一定程度上影响参考点的调整; 若参数r过大, 则可能出现多个参考点处于同一邻域内; 为了避免此类情况发生, 本文还根据调整后的参考点数量动态改变参数r, 直到每一个参考点处于不同的邻域内.

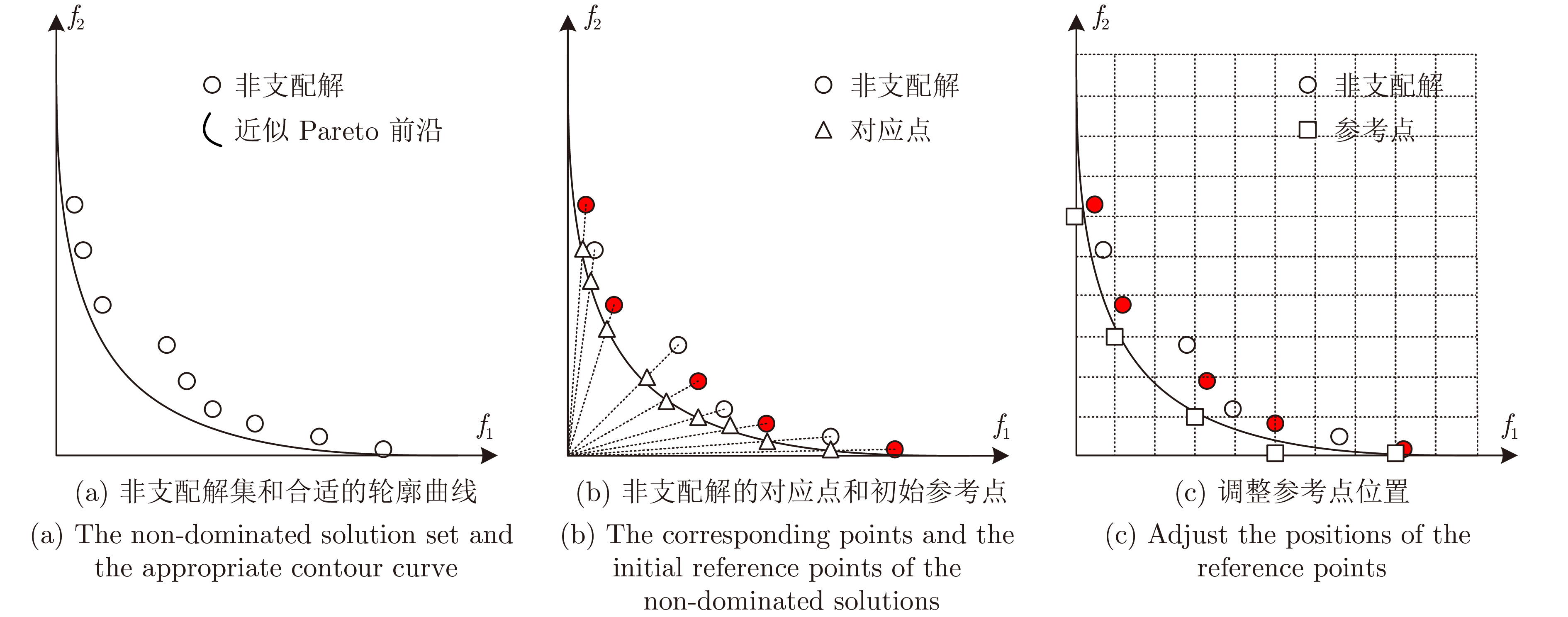
为了更清楚地理解参考点自适应过程, 图3给出一个两目标优化问题的例子说明如何进行参考点自适应. 图3(a)为一组非支配解, 根据非支配解的分布确定合适的轮廓曲线近似PF; 在曲线上找到所有非支配解的对应点, 即非支配解和原点之间的连线与曲线的交点, 然后根据多样性评估准则选择一组分布广泛且均匀的初始参考点, 如图3(b)所示, 实心圆形即为初始参考点; 由于PF形状为凸型, 因此将初始参考点调整为所在邻域的理想点, 如图3(c).

图 3 自适应参考点过程

Fig. 3 Adaptive reference point process

2.5 确定轮廓曲线以及曲线参数p

轮廓曲线与PF的近似程度直接影响参考点的生成以及算法的性能, 闵氏距离能够覆盖各种凹凸度的PF, 因此本文利用闵氏距离预先估计PF形状. 算法5对如何确定一条特定的曲线做了具体描述, 首先利用m个边界解构建超平面; 然后计算该超平面与原点之间的欧氏距离d, 将所有候选解到原点的距离与距离d进行比较, 根据种群与超平面之间的位置关系初步判断PF的凹凸性, 并相应地确定曲线参数范围, 这一步的目的是缩小曲线参数的范围, 降低时间复杂度; 最后对于每一个p值, 计算所有解的闵氏距离方差, 选择方差最小时对应的p值作为曲线参数. 此时轮廓曲线可以用公式表示:

(17)

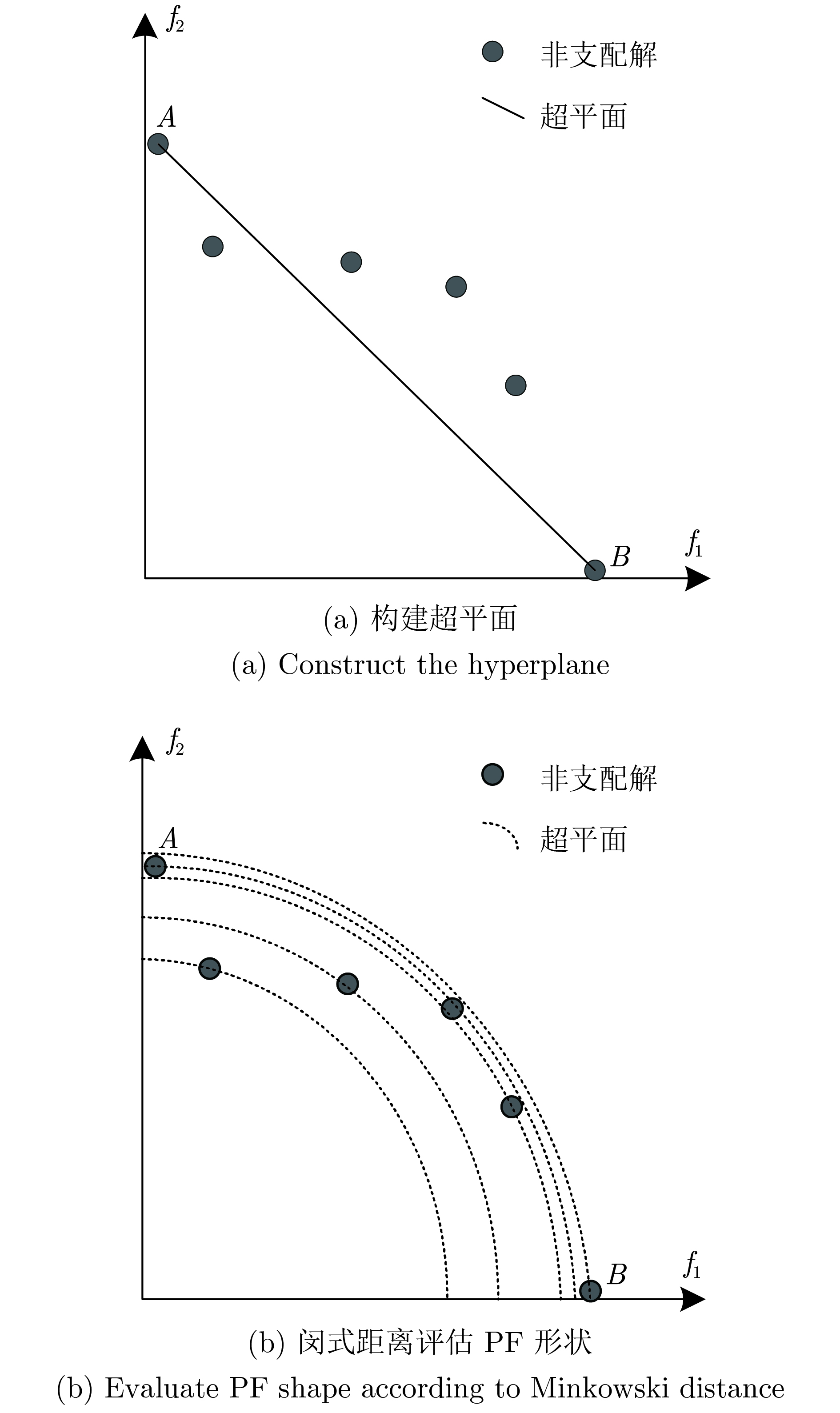
图4为一个两目标优化问题, 若要判断PF的形状, 首先连接边界点A、B构建超平面, 如图4(a)所示, 从图中可以看出, 种群中的个体大部分位于超平面的上方, 并且根据非支配解与原点之间的距离和超平面与原点之间的距离可以初步判断PF为凹型, 从而确定p的取值范围为{1, 1.1, 1.2, ···, 3}; 然后对于每一个p值, 计算所有非支配解的闵式距离方差, 如图4(b)所示, 方差越小, 解之间的轮廓曲线越接近.

图 4 确定轮廓曲线以及曲线参数

Fig. 4 Determine the contour curve and curve parameter

算法5. 轮廓曲线

输入: P (种群);

输出: p (曲线参数);

1) /*选择m个边界解构成一个超平面并计算该平面与原点之间的欧氏距离d*/

2) num1 = 与原点的距离小于d的解数量;

3) num2 = 与原点的距离大于d的解数量;

4) if num1 > num2

5) 　Cp = {0.1, 0.2, ···, 1};

7) 　Cp = {1, 1.1, 1.2, ···, 3};

8) else

9) 　p = 1;

10) end if

11) for i = 1 to length(Cp)

12) 　p = Cp[i];

13) 　for j = 1 to length(P)

14) 　　x = P[j];

15) 　　 $C_{p} [j] = (\sum_{u = 1}^{m} {f_{u}}^{'} {(x)}^{p})^{1 / p}$ ;

16) 　end for

17) 　Vp[i] = Std(Cp);

18) end for

19) index = arg min(Vp);

20) return Cp[index];

2.6 算法的时间复杂度分析

算法MaOEA-IAR主要在环境选择中耗费时间, 其中生成参考点的最大时间复杂度为O(MrN), M为目标数, r为邻域参数, $N$ 为种群规模; 确定轮廓曲线以及曲线参数的时间复杂度为O(CpN), Cp为曲线参数数量; 计算指标值的时间复杂度为O(N); 因此算法的时间复杂度为max(O(MrN)).

3. 实验研究与结果分析

在这一部分, 将本文提出的算法与当前性能较好的先进算法进行实验对比, 对比算法分别为: MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA, 实验取自DTLZ测试集和WFG测试集以及IDTLZ1、IDTLZ2. 接下来首先介绍实验设置, 然后对测试集中具有规则PF的测试问题的实验结果和算法对比进行分析, 之后对测试集中具有不规则PF的测试问题的实验结果和算法对比进行分析, 最后对比同样采用参考点自适应方法的算法AR-MOEA和MaOEA-IAR的运行时间, 进一步增加算法性能的说服力. 除此之外, 为了说明参考点自适应策略的有效性, 对比AR-MOEA与MaOEA-IAR在MaF测试集上的性能.

3.1 实验设置

1)基准测试问题: 本文采用DTLZ测试集中的测试问题DTLZ1~DTLZ7和WFG测试集中的测试问题WFG1~WFG9以及IDTLZ1、IDTLZ2, 这些测试问题的目标数目可以任意扩展, 实验重点研究目标数为5、10、15、25的测试问题, 表1给出了每个测试问题的真实PF形状以及不同目标数目下各个测试问题对应的决策变量数.

表 1 测试问题

Table 1 Test questions

问题	目标数目M	决策变量D	PF
DTLZ1	5, 10, 15, 25	M−1+5	线性
DTLZ2~DTLZ4	5, 10, 15, 25	M−1+10	凹型
DTLZ5~DTLZ6	5, 10, 15, 25	M−1+10	退化
DTLZ7	5, 10, 15, 25	M−1+20	断开
IDTLZ1	5, 10, 15, 25	M−1+5	倒置
IDTLZ2	5, 10, 15, 25	M−1+10	倒置
WFG1	5, 10, 15, 25	M−1+10	混合
WFG2	5, 10, 15, 25	M−1+10	断开
WFG3	5, 10, 15, 25	M−1+10	退化
WFG4~DTLZ9	5, 10, 15, 25	M−1+10	凹型

2)种群规模: 对比算法MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA与MaOEA-IAR的种群规模取决于参考向量的数量, 参考向量的数量由外层和内层的划分数目H1、H2决定, 表2总结了不同目标数目下对应的种群规模.

表 2 不同目标对应的种群规模

Table 2 Population sizes corresponding to different objectives

目标数目M	(H1, H2)	种群规模N
5	(6, 0)	126
10	(3, 2)	275
15	(2, 1)	135
25	(2, 1)	350

3)交叉和变异算子: 在本文用到的所有进化算法均采用二进制交叉[37]和多项式变异[38]生成子代, 交叉概率和变异概率设置为1.0和1/D(决策变量数目), 分布指标都设置为20.

4)终止条件: 每一次运行的终止条件是最大评价次数, 评价次数为进化代数与种群规模的乘积, 对于不同的目标数目所采用的进化代数不同, 具体的设置如表3所示.

表 3 不同目标对应的终止条件

Table 3 Termination conditions corresponding to different objectives

目标数目M	种群规模N	进化代数	评价次数
5	126	800	100800
10	275	1000	275000
15	135	1300	175500
25	350	1500	525000

5)评价指标: 算法性能由IGD指标[22]和PD指标[34]评估. IGD指标为同时衡量种群收敛性和多样性的指标, 在IGD指标计算中, 对于每个测试实例, 利用Das和Dennis在[39]中提出的方法(在10目标、15目标和25目标测试问题中, 采用双层参考点采用方法)在PF上采样大约5000个均匀分布的参考点, 计算距离每个参考点最近的解与参考点之间的欧氏距离的平均值; 为了进一步证明本文提出的方法在生成均匀参考点方面的有效性, 采用PD指标单独衡量种群的多样性, PD指标利用Lp标准距离计算解的差异, 通过种群中解的差异性的累加衡量多样性.

6)统计方法: 每个算法在每个测试问题上独立运行30次, 采用Wilcoxon秩和检验方法比较本文提出算法与现存算法之间的性能, 均值分析的显著性水平设置为0.05.

7)对比算法参数设置: 对于MOEA-DD, 选择局部父代概率δ设置为0.9; 对于RVEA, 控制惩罚概率参数α设置为2, 参考向量自适应的频率fr设置为0.1; 对于MOMBI-II, 差异门限α设置为0.5, 公差门限ε设置为0.001, 最小向量记录规格设置为5.

3.2 算法在规则PF测试问题上的对比分析

根据表4的数据分析, 在具有规则PF的测试问题中, 虽然MaOEA-IAR没有在所有的测试问题上获得最好的性能, 但总体性能良好. DTLZ1为线性PF, AR-MOEA在该测试问题上指标值突出, 这与AR-MOEA采用的参考点更新方法有关, 在线性PF上, 初始均匀分布的参考点不会被档案中的候选解更新; DTLZ2为凹型PF, MaOEA-IAR在5目标和25目标上获得最好性能, AR-MOEA在其余目标上获得最好性能; DTLZ3为凹型PF, 该测试问题测试算法能否收敛到Pareto全局最优, 在该测试问题中, AR-MOEA表现最好; DTLZ4依然为凹型PF, 测试当PF高度偏向的情况下算法能否确保最优解均匀分布, 从表中可观察到MaOEA-IAR在10目标、15目标和25目标上获得最优性能, 说明该算法在保持解均匀分布的能力上优于其他算法; WFG4~WFG9为凹型PF, 且与现实优化问题相似, 在此类测试问题上, MaOEA-IAR在大部分测试问题上能够获得最好性能, 这是由于基于PF形状的多样性评估准则能够准确地评估解之间的多样性. 综合统计结果, 在具有规则PF的测试问题中, 虽然MaOEA-IAR没有在每一个测试问题上获得最好的性能, 但总体性能良好, 尤其在WFG测试问题中的性能显著.

表 4 MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA以及MaOEA-IAR在DTLZ1~DTLZ4, WFG4~WFG9上获得IGD值的统一结果(均值和标准差). 最好的结果已被标记

Table 4 The statistical results (mean and standard deviation) of the IGD values obtained by MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA and MaOEA-IAR on DTLZ1~DTLZ4, WFG4~WFG9. The best results are highlighted

问题	M	MOEA-DD	NSGA-III	RVEA	MOMBI-II	AR-MOEA	MaOEA-IAR
DTLZ1	5	6.3354×10−2 (8.24×10−5)+	6.3588×10−2 (2.93×10−4)+	6.3365×10−2 (1.44×10−4)+	6.7530×10−2 (8.96×10−3)+	1.3555×10−3 (7.87×10−6)+	2.6870×10−1 (7.95×10−2)
	10	1.0784×10−1 (3.02×10−4)+	1.2073×10−1 (2.91×10−2)+	1.0804×10−1 (1.45×10−3)+	2.1744×10−1 (2.32×10−2)+	1.3680×10−3 (1.14×10−4)+	4.7099×10+1 (1.33×10+1)
	15	1.4088×10−1 (5.94×10−3)+	1.9693×10−1 (2.97×10−2)+	1.6130×10−1 (7.54×10−3)+	2.8789×10−1 (3.92×10−2)+	3.1383×10−3 (1.58×10−3)+	5.6383×10+1 (2.03×10+1)
	25	1.0354×10−1 (5.86×10−2)+	2.7045×10−1 (1.96×10−1)=	1.3372×10−1 (7.61×10−2)+	2.0490×10−1 (1.19×10−1)+	1.2392×10−1 (7.02×10−2)+	2.4067×10−1 (1.44×10−1)
DTLZ2	5	1.9506×10−1 (8.00×10−5)+	1.9538×10−1 (1.18×10−4)+	1.9508×10−1 (7.34×10−5)+	2.0140×10−1 (1.93×10−3)=	4.3609×10−3 (7.50×10−6)+	2.0137×10−1 (1.61×10−3)
	10	4.2179×10−1 (8.12×10−4)−	4.4544×10−1 (3.60×10−2)−	4.2291×10−1 (1.61×10−3)−	4.4619×10−1 (6.50×10−3)−	4.9235×10−2 (1.43×10−4)−	4.7588×10−2 (4.60×10−4)
	15	6.1801×10−1 (1.88×10−2)−	6.4108×10−1 (2.01×10−2)−	6.3958×10−1 (3.67×10−2)−	8.5287×10−1 (6.41×10−2)−	1.0058×10−2 (1.56×10−3)=	1.1135×10−2 (1.23×10−3)
	25	4.3015×10−1 (2.45×10−1)−	5.3577×10−1 (3.10×10−1)−	4.3033×10−1 (2.45×10−1)−	7.0528×10−1 (4.12×10−1)−	6.1891×10−1 (3.45×10−1)−	4.2923×10−1 (2.44×10−1)
DTLZ3	5	1.9907×10−1 (3.45×10−3)+	7.1945×10−1 (1.21×10+0)+	2.0829×10−1 (2.11×10−2)+	2.0571×10−1 (4.19×10−3)+	4.4165×10−3 (5.43×10−5)+	1.0190×10+0 (6.60×10−1)
	10	4.2392×10−1 (3.09×10−3)+	1.1841×10+0 (1.08×10+0)+	4.3390×10−1 (1.54×10−2)+	6.9344×10−1 (1.66×10−1)+	3.1091×10−2 (9.02×10−2)+	4.8634×10+2 (9.91×10+1)
	15	6.6842×10−1 (2.26×10−1)+	5.5656×10+0 (2.83×10+0)+	8.3685×10−1 (3.72×10−1)+	1.1033×10+0 (2.16×10−2)+	3.8594×10−1 (5.94×10−1)+	6.4283×10+2 (1.08×10+2)
	25	4.3041×10−1 (2.46×10−1)+	8.3189×10+0 (6.16×10+0)−	4.3076×10−1 (2.46×10−1)+	8.7119×10−1 (5.08×10−1)+	4.6567×10−1 (2.38×10−1)+	9.8829×10−1 (5.81×10−1)
DTLZ4	5	1.9508×10−1 (9.98×10−5)+	2.4346×10−1 (9.84×10−2)−	1.9514×10−1 (1.62×10−4)+	2.5703×10−1 (9.71×10−2)−	4.4014×10−3 (1.06×10−4)+	2.0129×10−1 (1.72×10−3)
	10	4.2271×10−1 (1.73×10−3)−	4.5035×10−1 (3.18×10−2)−	4.3317×10−1 (2.13×10−3)−	4.5814×10−1 (1.71×10−2)−	5.7202×10−3 (5.61×10−4)−	5.6898×10−3 (1.01×10−4)
	15	6.3495×10−1 (1.18×10−2)−	6.4865×10−1 (2.13×10−2)−	6.3283×10−1 (7.39×10−3)−	6.5937×10−1 (2.31×10−2)−	1.1470×10−2 (1.34×10−3)−	9.9175×10−3 (1.41×10−3)
	25	4.3041×10−1 (2.45×10−1)−	4.6255×10−1 (2.72×10−1)−	4.3053×10−1 (2.46×10−1)−	4.3098×10−1 (2.46×10−1)−	5.8948×10−1 (2.86×10−1)−	4.3021×10−1 (2.44×10−1)
WFG4	5	1.2337×10+0 (4.54×10−3)−	1.1663×10+0 (3.61×10−3)−	1.1649×10+0 (2.28×10−3)−	1.8356×10+0 (2.02×10−1)−	1.1244×10+0 (1.47×10−2)−	1.1192×10+0 (2.58×10−1)
	10	6.0999×10+0 (1.66×10−1)−	4.5156×10+0 (4.39×10−2)−	4.3816×10+0 (5.05×10−2)−	5.6693×10+0 (4.27×10−1)−	4.5463×10+0 (9.53×10−3)−	4.0153×10+0 (2.71×10−2)
	15	9.4478×10+0 (7.47×10−1)−	9.1431×10+0 (9.63×10−2)−	9.4338×10+0 (3.83×10−1)−	2.0211×10+1 (1.35×10+0)−	9.3716×10+0 (3.68×10−2)−	8.4000×10+0 (1.11×10−1)
	25	2.4032×10+1 (2.95×10−1)−	1.3110×10+1 (7.97×10−1)−	1.2394×10+1 (2.92×10−1)−	3.7271×10+1 (3.18×10+0)−	1.5196×10+1 (2.61×10−1)−	1.1405×10+1 (1.89×10−2)
WFG5	5	1.2116×10+0 (6.46×10−3)−	1.1459×10+0 (4.71×10−3)−	1.1554×10+0 (2.17×10−3)−	1.5867×10+0 (1.16×10−1)−	1.1648×10+0 (2.17×10−4)−	1.1148×10+0 (1.31×10−2)
	10	6.2798×10+0 (1.39×10−1)−	4.4654×10+0 (1.82×10−2)−	4.3730×10+0 (4.27×10−2)−	5.3610×10+0 (2.19×10−2)−	4.5296×10+0 (9.52×10−3)−	3.9834×10+0 (1.90×10−2)
	15	1.1246×10+1 (1.85×10−1)−	8.9556×10+0 (7.70×10−2)−	9.8645×10+0 (1.66×10−1)−	2.4601×10+1 (1.34×10+0)−	9.3564×10+0 (5.48×10−2)−	8.2316×10+0 (8.70×10−2)
	25	2.2399×10+1 (1.96×10−1)−	1.1842×10+1 (1.14×10+0)=	1.1407×10+1 (5.45×10−2)=	4.5754×10+1 (3.19×10+0)−	1.4772×10+1 (2.79×10−1)−	1.1370×10+1 (3.12×10−3)
WFG6	5	1.2276×10+0 (1.14×10−2)−	1.1617×10+0 (2.62×10−3)−	1.1638×10+0 (2.18×10−3)−	2.1021×10+0 (3.69×10−1)−	1.1624×10+0 (1.24×10−3)−	1.1443×10+0 (2.89×10−2)
	10	6.0366×10+0 (1.65×10−1)−	4.5795×10+0 (1.88×10−2)−	4.4020×10+0 (7.33×10−2)−	5.2873×10+0 (2.86×10−2)−	4.5333×10+0 (1.12×10−2)−	4.0605×10+0 (4.78×10−2)
	15	1.0818×10+1 (1.01×10+0)−	9.3642×10+0 (3.84×10−1)−	1.0520×10+1 (4.62×10−1)−	1.8732×10+1 (1.89×10+0)−	9.3953×10+0 (5.07×10−2)−	8.5397×10+0 (1.76×10−1)
	25	2.1950×10+1 (6.43×10−1)−	1.5582×10+1 (9.19×10−1)−	1.5281×10+1 (9.27×10−1)−	3.5035×10+1 (2.81×10+0)−	1.5206×10+1 (3.56×10−1)−	1.1375×10+1 (1.29×10−2)
WFG7	5	1.2454×10+0 (8.15×10−3)−	1.1680×10+0 (3.67×10−3)−	1.1693×10+0 (3.05×10−3)−	1.8487×10+0 (2.46×10−1)−	1.1787×10+0 (8.19×10−4)−	1.1499×10+0 (3.17×10−2)
	10	5.1499×10+0 (2.73×10−1)−	4.5094×10+0 (3.76×10−2)−	4.3149×10+0 (5.44×10−2)−	5.4063×10+0 (5.76×10−2)−	4.5123×10+0 (1.07×10−2)−	3.9423×10+0 (4.82×10−2)
	15	8.9281×10+0 (8.74×10−2)−	9.0694×10+0 (9.98×10−2)−	9.1250×10+0 (2.71×10−1)−	1.7892×10+1 (1.65×10+0)−	9.4000×10+0 (3.81×10−2)−	8.7103×10+0 (1.27×10−1)
	25	1.6767×10+1 (1.55×10+0)−	1.3522×10+1 (7.95×10−1)−	1.1672×10+1 (3.01×10−1)=	3.2655×10+1 (2.66×10+0)−	1.5873×10+1 (1.94×10−1)−	1.1572×10+1 (8.12×10−2)
WFG8	5	1.2301×10+0 (8.57×10−3)−	1.1867×10+0 (9.32×10−2)=	1.1770×10+0 (4.82×10−3)−	2.9462×10+0 (3.23×10−2)−	1.1575×10+0 (2.95×10−3)−	1.1675×10+0 (1.66×10−2)
	10	5.2132×10+0 (3.48×10−1)−	4.5532×10+0 (3.00×10−1)−	4.3661×10+0 (8.88×10−2)−	6.0943×10+0 (8.02×10−1)−	4.6273×10+0 (4.43×10−2)−	4.1413×10+0 (7.20×10−2)
	15	9.2706×10+0 (3.66×10−1)−	9.1735×10+0 (4.45×10−1)−	9.9548×10+0 (7.95×10−1)−	2.0437×10+1 (1.84×10+0)−	9.3736×10+0 (7.14×10−2)−	8.7680×10+0 (2.43×10−1)
	25	2.2579×10+1 (3.17×10+0)−	1.6519×10+1 (6.99×10−1)−	1.3760×10+1 (1.73×10+0)−	3.9378×10+1 (2.20×10+0)−	1.5213×10+1 (2.84×10−1)−	1.1409×10+1 (2.03×10−2)
WFG9	5	1.2087×10+0 (1.17×10−2)−	1.1112×10+0 (1.08×10−2)−	1.1315×10+0 (4.39×10−3)−	2.6613×10+0 (1.67×10−1)−	1.1476×10+0 (2.59×10−3)−	1.0867×10+0 (1.42×10−2)
	10	5.2551×10+0 (3.81×10−1)−	4.3117×10+0 (7.01×10−2)−	4.3306×10+0 (6.41×10−2)−	5.2773×10+0 (6.59×10−2)−	4.4943×10+0 (1.01×10−2)−	3.8995×10+0 (3.21×10−2)
	15	8.9598×10+0 (5.37×10−1)−	8.6320×10+0 (1.41×10−1)−	8.8404×10+0 (2.73×10−1)−	2.5164×10+1 (1.97×10+0)−	9.1233×10+0 (3.81×10−2)−	8.1162×10+0 (1.37×10−1)
	25	1.5766×10+1 (3.46×10+0)−	1.2211×10+1 (7.44×10−1)−	1.2343×10+1 (1.28×10+0)−	4.8512×10+1 (2.40×10+0)−	1.5086×10+1 (2.89×10−1)−	1.1166×10+1 (8.75×10−2)
+/−/=		10/30/0	7/30/3	10/28/2	8/31/1	10/29/1
“+”表明该算法优于MaOEA-IAR, “−”劣于MaOEA-IAR, “=”则表示与MaOEA-IAR性能相似

根据表5的数据分析, 在多样性方面, 本文提出的算法能在大部分问题中表现良好, 尤其是在高维空间中, MaOEA-IAR相较于其他算法而言性能显著. MOEA-DD在25目标的DTLZ1和10目标的DTLZ4上面获得最好性能; NSGA-III在5目标和25目标的DTLZ3上获得最好性能; MaOEA-IAR在剩余的所有目标的测试问题中获得最好性能. 可以看出在高维空间中, 本文提出的自适应参考点方法所生成的参考点多样性好, 相应的种群多样性也有一定提升.

表 5 MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA以及MaOEA-IAR在DTLZ1~DTLZ4, WFG4~WFG9上获得PD值的统一结果(均值和标准差). 最好的结果已被标记

Table 5 The statistical results (mean and standard deviation) of the PD values obtained by MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA and MaOEA-IAR on DTLZ1~DTLZ4, WFG4~WFG9. The best results are highlighted

问题	M	MOEA-DD	NSGA-III	RVEA	MOMBI-II	AR-MOEA	MaOEA-IAR
DTLZ1	5	7.0347×10+5 (1.50×10+5)−	6.6822×10+5 (2.89×10+5)−	1.0144×10+6 (2.23×10+5)−	6.5737×10+5 (5.56×10+5)−	3.1124×10+5 (1.14×10+5)−	1.1335×10+7 (2.48×10+7)
	10	3.9493×10+9 (4.51×10+8)−	4.3920×10+9 (1.31×10+9)−	4.4832×10+9 (5.54×10+8)−	1.3231×10+8 (1.60×10+8)−	3.9031×10+9 (3.47×10+8)−	2.1838×10+12 (4.55×10+11)
	15	2.0771×10+11 (2.15×10+10)−	7.2781×10+10 (4.17×10+10)−	1.8665×10+11 (5.48×10+10)−	2.8086×10+8 (4.77×10+8)−	5.4706×10+10 (1.65×10+10)−	2.4099×10+13 (8.65×10+12)
	25	4.2240×10+13 (1.16×10+12)+	2.4959×10+13 (1.82×10+13)+	1.5947×10+13 (3.82×10+12)+	2.6381×10+9 (4.68×10+9)−	1.2365×10+13 (6.44×10+12)+	1.6674×10+11 (4.44×10+11)
DTLZ2	5	4.5169×10+6 (3.69×10+5)−	4.1624×10+6 (5.12×10+5)−	4.4519×10+6 (4.97×10+5)−	3.1301×10+6 (4.36×10+5)−	2.2535×10+6 (1.23×10+5)−	1.3815×10+7 (1.83×10+6)
	10	1.0700×10+10 (4.94×10+8)−	1.5036×10+10 (4.96×10+9)−	1.4787×10+10 (8.21×10+8)−	6.3297×10+9 (9.76×10+8)−	1.4371×10+10 (9.34×10+8)−	4.8565×10+10 (8.50×10+9)
	15	2.3742×10+11 (5.12×10+10)−	5.4986×10+10 (3.53×10+10)−	1.5788×10+11 (3.98×10+10)−	1.4169×10+9 (1.60×10+9)−	2.2431×10+10 (1.21×10+10)−	4.6071×10+11 (2.42×10+11)
	25	1.5327×10+13 (1.82×10+12)−	1.9112×10+13 (9.88×10+12)−	1.8880×10+13 (3.09×10+12)−	1.4360×10+10 (2.20×10+10)−	2.1209×10+12 (1.31×10+12)−	1.0367×10+15 (3.68×10+13)
DTLZ3	5	1.0522×10+7 (3.37×10+6 )+	1.8368×10+7 (1.98×10+7 )+	9.1974×10+6 (3.08×10+6 )+	2.8101×10+6 (4.82×10+5 )+	3.0005×10+6 (3.36×10+5 )+	2.0182×10+6 (4.79×10+6)
	10	1.3601×10+10 (2.86×10+9)−	2.2578×10+10 (1.68×10+10)−	1.6599×10+10 (2.67×10+9)−	1.1037×10+9 (1.66×10+9)−	4.7006×10+9 (1.96×10+9)−	2.9582×10+13 (4.66×10+12)
	15	3.6156×10+11 (8.59×10+11)−	1.1462×10+12 (8.77×10+11)−	1.2788×10+11 (2.39×10+11)−	3.1557×10+8 (4.47×10+8)−	4.9753×10+10 (4.57×10+10)−	6.5391×10+14 (1.63×10+14)
	25	1.6252×10+13 (1.40×10+12)+	3.2406×10+15 (2.26×10+15)+	1.0735×10+13 (5.81×10+12)+	7.3339×10+8 (1.67×10+9)−	2.2266×10+13 (2.19×10+13)+	9.6558×10+10 (2.77×10+11)
DTLZ4	5	3.7620×10+6 (6.71×10+5)−	3.3390×10+6 (8.43×10+5)−	4.4024×10+6 (6.07×10+5)−	2.1806×10+6 (1.14×10+6)−	2.4008×10+6 (1.56×10+5)−	1.3225×10+7 (1.43×10+6)
	10	1.3637×10+10 (1.08×10+9)+	5.6960×10+9 (2.42×10+9)−	1.0848×10+10 (2.29×10+9)+	5.9777×10+7 (2.68×10+7)−	4.0114×10+9 (1.10×10+9)−	9.1937×10+9 (2.85×10+9)
	15	2.7750×10+9 (1.79×10+9)−	5.2847×10+8 (5.23×10+8)−	2.0648×10+9 (1.07×10+9)−	4.0923×10+7 (1.33×10+8)−	5.8144×10+9 (3.64×10+9)−	3.9392×10+10 (1.98×10+10)
	25	3.7432×10+12 (9.47×10+11)−	3.1839×10+11 (3.51×10+11)−	3.8552×10+11 (1.51×10+11)−	2.8053×10+8 (5.19×10+8)−	1.2420×10+11 (5.99×10+10)−	8.4925×10+14 (3.45×10+13)
WFG4	5	1.2326×10+8 (6.16×10+6)−	1.3502×10+8 (4.43×10+6)−	1.2748×10+8 (7.49×10+6)−	1.8889×10+7 (3.43×10+6)−	6.4422×10+7 (4.60×10+6)−	2.0686×10+8 (1.12×10+7)
	10	1.4338×10+11 (9.29×10+9)−	2.9001×10+11 (1.68×10+10)−	1.9392×10+11 (1.22×10+10)−	7.4282×10+10 (2.70×10+10)−	1.4488×10+11 (8.57×10+9)−	6.6989×10+11 (2.52×10+10)
	15	3.4224×10+12 (5.49×10+11)−	5.5478×10+12 (7.84×10+11)−	4.0484×10+12 (1.04×10+12)−	2.0839×10+10 (1.96×10+10)−	2.0698×10+12 (6.60×10+11)−	1.9906×10+13 (1.68×10+12)
	25	9.4061×10+13 (1.83×10+13)−	2.2238×10+15 (6.40×10+14)−	1.6309×10+14 (2.64×10+13)−	2.5978×10+11 (6.99×10+11)−	3.9968×10+14 (1.07×10+14)−	1.0349×10+16 (5.36×10+14)
WFG5	5	1.2123×10+8 (6.36×10+6)−	1.4121×10+8 (8.96×10+6)−	1.1886×10+8 (4.50×10+6)−	2.3887×10+7 (4.70×10+6)−	4.1612×10+7 (3.93×10+6)−	1.9277×10+8 (1.04×10+7)
	10	1.9457×10+11 (1.24×10+10)−	3.7692×10+11 (1.60×10+10)−	2.2741×10+11 (1.20×10+10)−	1.1103×10+11 (8.12×10+9)−	1.2033×10+11 (6.96×10+9)−	6.8603×10+11 (3.29×10+10)
	15	3.9863×10+12 (7.29×10+11)−	8.8868×10+12 (7.95×10+11)−	4.9690×10+12 (3.43×10+11)−	2.0497×10+10 (3.24×10+10)−	1.4482×10+12 (4.81×10+11)−	2.0970×10+13 (1.56×10+12)
	25	2.8409×10+14 (2.86×10+13)−	1.6088×10+15 (7.01×10+14)−	2.7765×10+14 (3.00×10+13)−	1.1499×10+12 (2.16×10+12)−	5.7645×10+14 (6.09×10+13)−	1.2220×10+16 (5.00×10+14)
WFG6	5	1.1994×10+8 (8.37×10+6)−	1.2908×10+8 (1.30×10+7)−	1.1997×10+8 (7.99×10+6)−	1.7038×10+7 (6.02×10+6)−	5.4499×10+7 (6.80×10+6)−	1.8108×10+8 (1.37×10+7)
	10	1.6619×10+11 (1.38×10+10)−	2.7497×10+11 (1.56×10+10)−	1.9869×10+11 (1.18×10+10)−	9.2008×10+10 (6.73×10+9)−	1.1142×10+11 (6.52×10+9)−	6.2142×10+11 (2.98×10+10)
	15	3.5945×10+12 (7.09×10+11)−	4.3937×10+12 (8.35×10+11)−	2.6933×10+12 (5.32×10+11)−	4.3260×10+10 (8.15×10+10)−	5.8023×10+11 (5.03×10+11)−	1.7544×10+13 (1.37×10+12)
	25	5.8142×10+13 (1.39×10+13)−	2.2239×10+15 (4.43×10+14)−	1.3831×10+14 (3.12×10+13)−	1.0474×10+12 (4.06×10+12)−	1.3621×10+14 (5.09×10+13)−	1.0081×10+16 (4.97×10+14)
WFG7	5	1.4307×10+8 (8.30×10+6)−	1.5328×10+8 (1.08×10+7)−	1.3594×10+8 (7.42×10+6)−	2.0429×10+7 (7.25×10+6)−	8.4724×10+7 (5.77×10+6)−	2.0010×10+8 (1.05×10+7)
	10	2.5289×10+11 (1.42×10+10)−	3.8153×10+11 (3.44×10+10)−	2.6215×10+11 (1.24×10+10)−	1.2614×10+11 (9.82×10+9)−	1.8152×10+11 (7.90×10+9)−	6.9190×10+11 (3.57×10+10)
	15	5.8545×10+12 (7.41×10+11)−	9.3356×10+12 (1.86×10+12)−	7.4133×10+12 (1.39×10+12)−	6.2349×10+10 (7.43×10+10)−	2.2599×10+12 (9.62×10+11)−	1.4999×10+13 (1.54×10+12)
	25	6.8227×10+14 (1.72×10+14)−	1.8449×10+15 (4.42×10+14)−	7.9199×10+14 (1.16×10+14)−	2.3362×10+12 (5.57×10+12)−	8.9765×10+14 (1.59×10+14)−	7.1165×10+15 (4.06×10+14)
WFG8	5	1.5013×10+8 (8.11×10+6)−	1.9783×10+8 (1.05×10+7)−	1.7829×10+8 (7.32×10+6)−	3.6308×10+7 (4.44×10+6)−	1.4408×10+8 (7.57×10+6)−	2.3335×10+8 (1.10×10+7)
	10	1.8219×10+11 (1.68×10+10)−	3.8567×10+11 (5.74×10+10)−	2.0046×10+11 (2.71×10+10)−	8.2783×10+10 (3.03×10+10)−	1.7126×10+11 (1.80×10+10)−	6.0173×10+11 (7.82×10+10)
	15	4.0400×10+12 (9.81×10+11)−	9.9234×10+12 (1.83×10+12)=	3.1853×10+12 (9.93×10+11)−	1.9227×10+11 (1.86×10+11)−	1.6871×10+12 (1.26×10+12)−	1.2895×10+13 (5.22×10+12)
	25	1.3971×10+14 (9.91×10+13)−	4.8077×10+15 (6.01×10+14)−	2.4789×10+14 (8.47×10+13)−	4.7555×10+12 (8.90×10+12)−	3.1451×10+14 (9.11×10+13)−	1.0680×10+16 (8.26×10+14)
WFG9	5	1.9141×10+8 (8.37×10+6)−	2.3341×10+8 (1.10×10+7)−	1.9389×10+8 (7.79×10+6)−	3.6203×10+7 (5.92×10+6)−	1.5846×10+8 (6.96×10+6)−	2.6391×10+8 (1.35×10+7)
	10	3.7972×10+11 (3.13×10+10)−	6.0898×10+11 (4.27×10+10)−	4.2790×10+11 (1.62×10+10)−	2.0148×10+11 (1.32×10+10)−	3.5255×10+11 (1.94×10+10)−	9.8787×10+11 (3.03×10+10)
	15	1.4912×10+13 (1.61×10+12)−	2.0973×10+13 (2.10×10+12)−	1.2833×10+13 (1.43×10+12)−	5.5018×10+10 (8.57×10+10)−	1.0318×10+13 (1.36×10+12)−	3.2318×10+13 (1.52×10+12)
	25	4.2407×10+15 (8.53×10+14)−	9.2528×10+15 (1.06×10+15)−	3.7876×10+15 (6.04×10+14)−	4.6745×10+12 (7.48×10+12)−	5.3764×10+15 (3.32×10+14)−	1.6297×10+16 (4.08×10+14)
+/−/=		4/36/0	3/36/1	4/36/0	1/39/0	3/37/0
“+”表明该算法优于MaOEA-IAR, “−”劣于MaOEA-IAR, “=”则表示与MaOEA-IAR性能相似

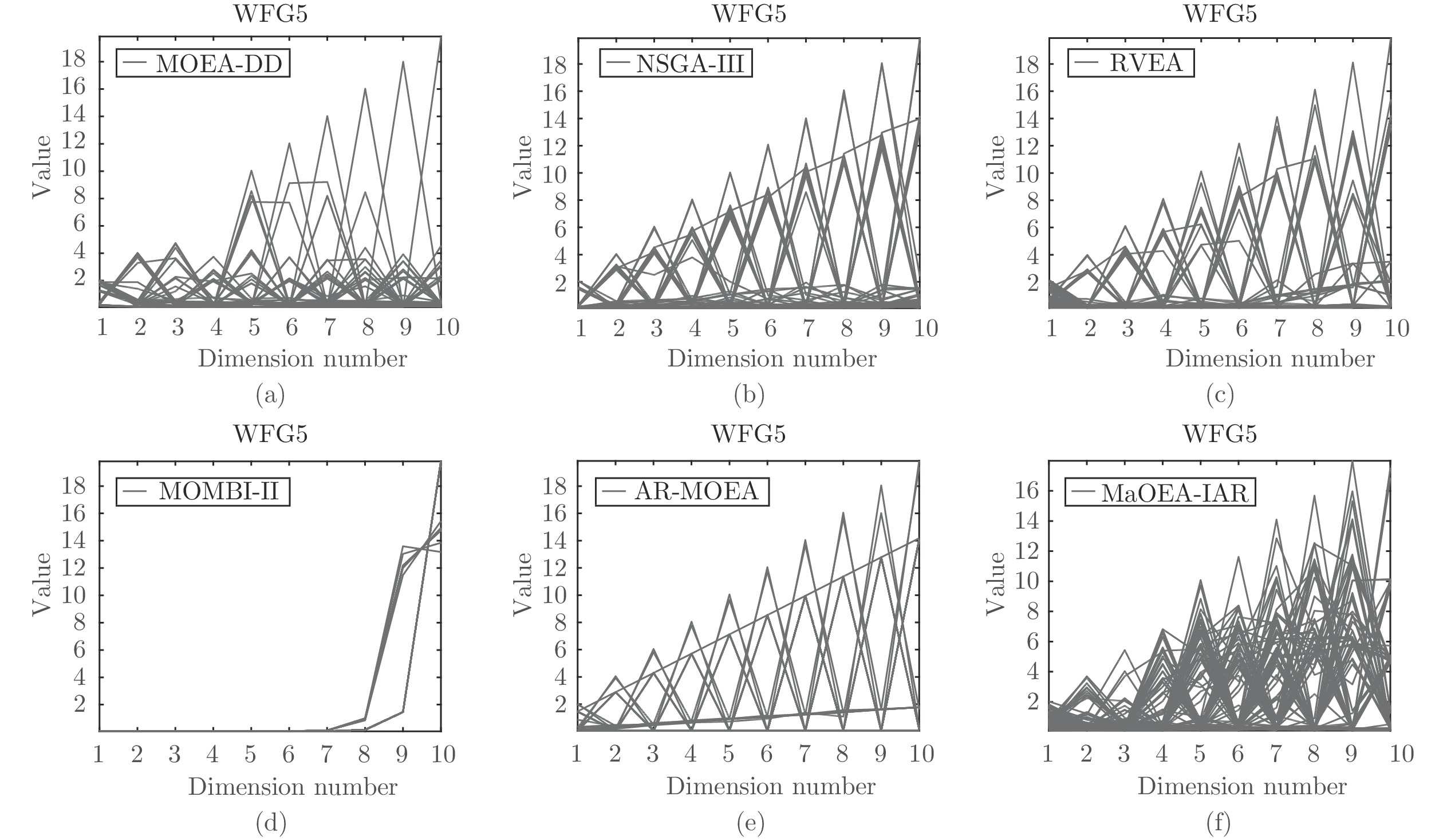
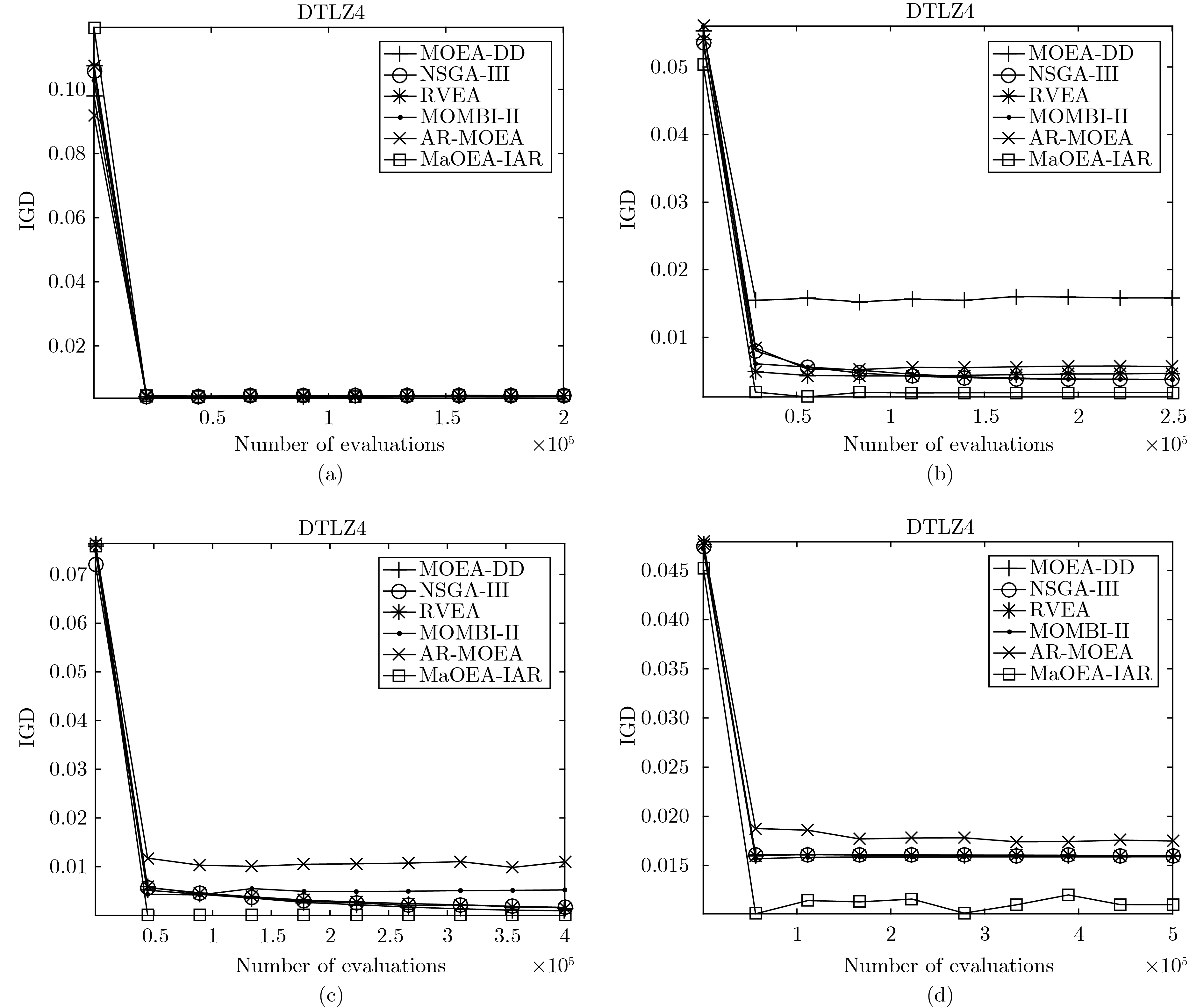
为了更直观地对比各个算法, 图5为6个算法在10目标WFG5上获得的非支配解的分布情况, 在平行坐标系中, 可以从收敛性、覆盖性、均匀性和扩展性4个方面来衡量种群质量[40]. 从图5可知6个算法都达到PF的范围, 无法准确地评估种群的收敛性; MOEA-DD、NSGA-III、RVEA、AR-MOEA、MaOEA-IAR的覆盖率较好, MOMBI-II在1~7目标轴上严重缺失解集, 覆盖率差; 在均匀性方面, 6个算法的平行坐标系下的折线都分布不均匀, 这并不意味着生成的种群不均匀, 因此在平行坐标系下无法比较种群的均匀性; 最后可以观察到6个算法目标值范围均为0~18, 可扩展性较好. 图6为6个算法在5、10、15、25目标的DTLZ4上获得的IGD指标轨迹, 从图中观察到算法MaOEA-IAR在5目标时与其他算法的性能相似, 随着目标数目的增加, MaOEA-IAR能够较快收敛到一个稳定且较低的IGD指标值.

图 5 WFG5问题10目标上获得的非支配解

Fig. 5 Nondominated solutions obtained on 10-objective WFG5

图 6 5、10、15、25目标DTLZ4问题上的IGD进化轨迹

Fig. 6 Evolutionary trajectories of IGD on 5、10、15、25-objective DTLZ4

3.3 算法在不规则PF测试问题上的对比分析

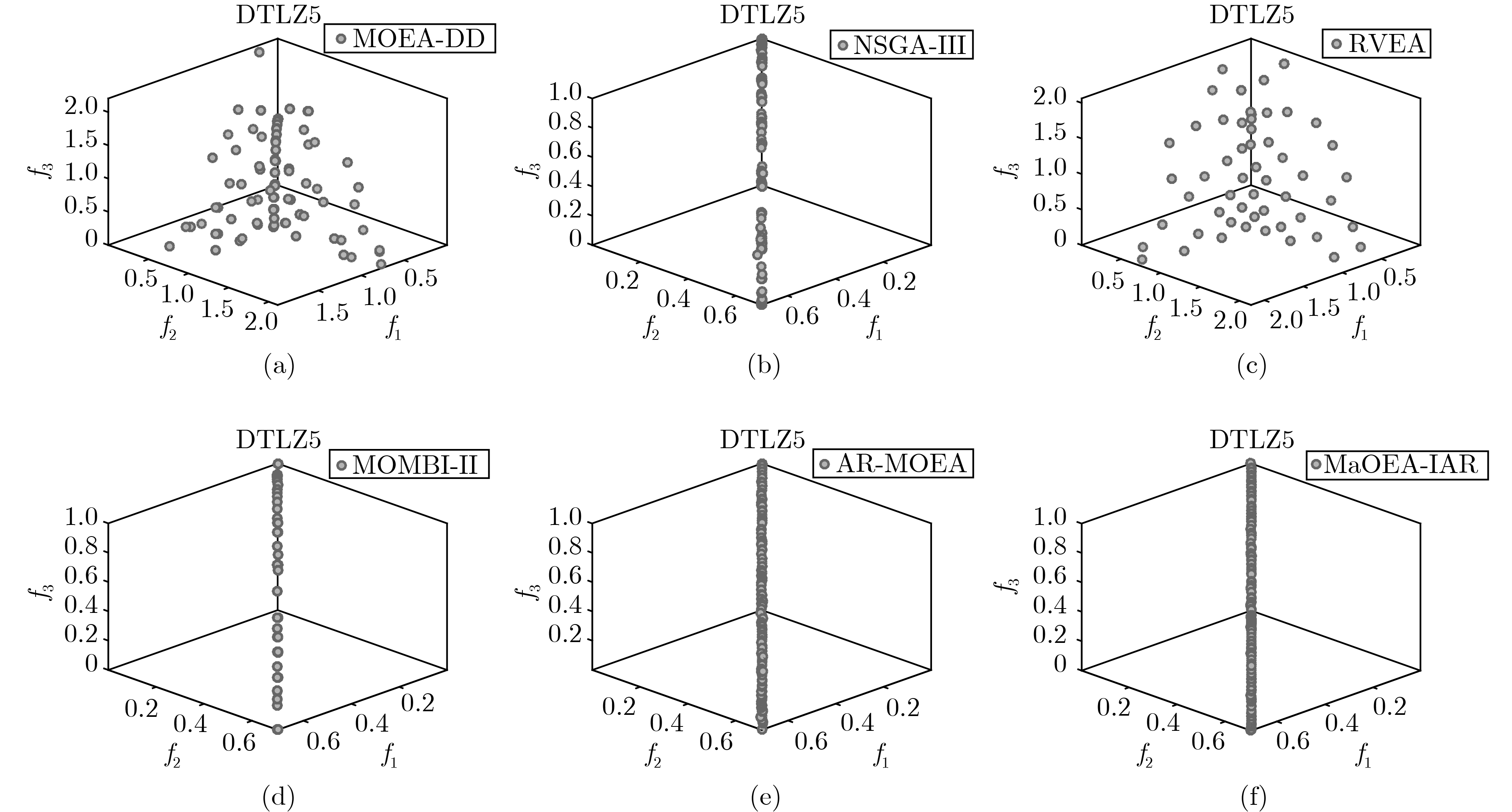
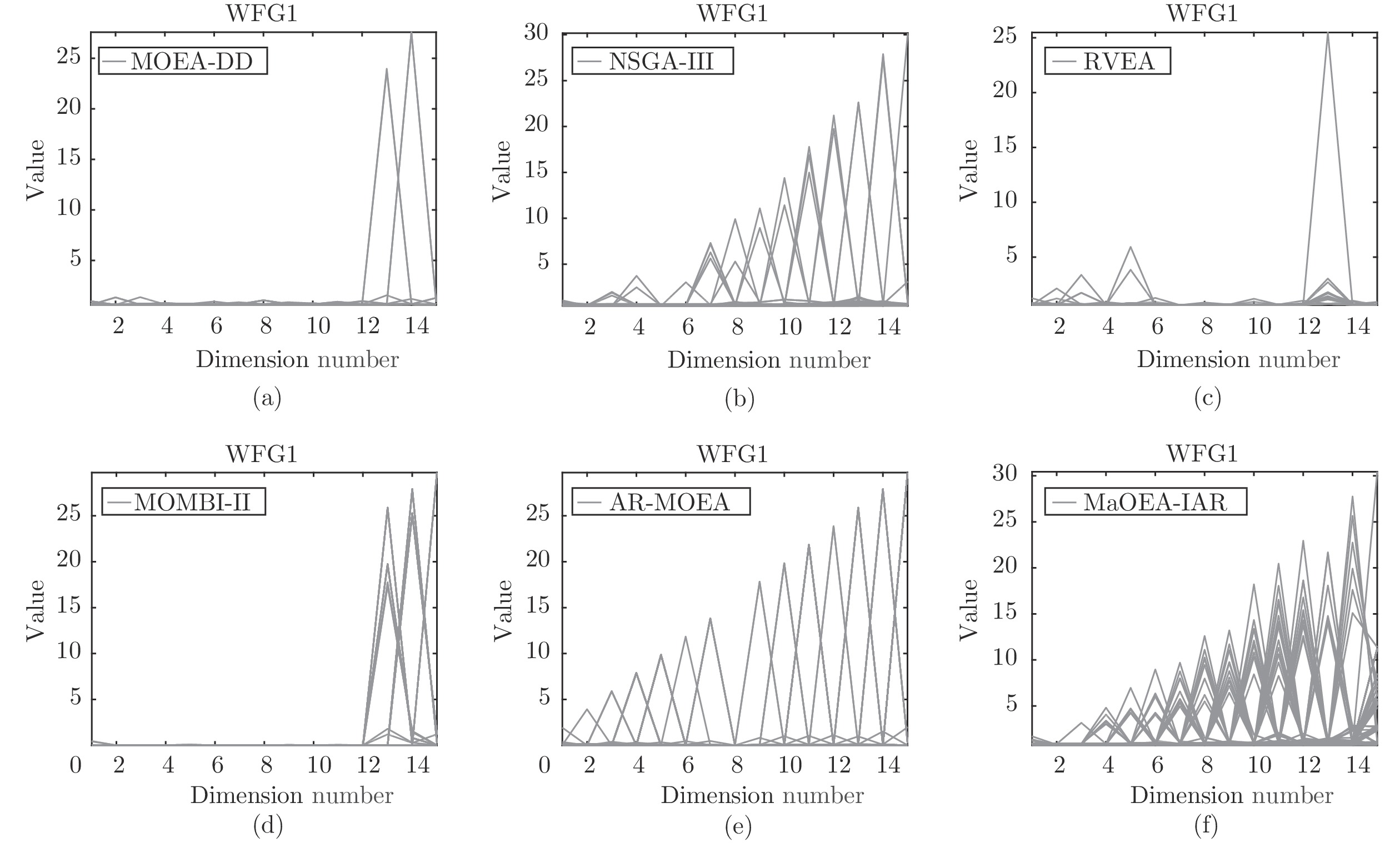
根据表6的数据分析结果, 在具有不规则PF的测试问题中, 虽然MaOEA-IAR没有在所有的测试问题获得最好的性能, 但总体上性能良好. DTLZ5~DTLZ6为退化PF, 此类测试问题测试进化算法收敛到Pareto最优曲线上的能力, 从表中可观察到, MaOEA-IAR在5目标、15目标、25目标的DTLZ5和25目标的DTLZ6上获得最好性能, MOEA-DD在5目标的DTLZ6上获得最好性能, AR-MOEA在其余目标上获得最好性能, 因此MaOEA-IAR虽然不能在所有目标的测试问题上得到最优性能, 但与其他算法相比, 该算法在处理具有退化PF的问题时依然能够得到较好的性能, 同时为了更直观地反应种群的分布情况, 图7描绘了各个算法在3目标DTLZ5上获得的非支配解的分布情况, 从图中可观察到MaOEA-IAR能够生成一组均匀且分布广泛的种群; DTLZ7为断开PF, 该测试问题测试算法在不同Pareto最优区域保持子种群的能力, 可观察到AR-MOEA能够在5目标、10目标和15目标上获得最好的性能, RVEA在25目标上获得最好性能, 但与剩余算法相比, MaOEA-IAR在不同区域保持子种群的能力更强; IDTLZ1~IDTLZ2为翻转PF, AR-MOEA在5目标的IDTLZ1上获得最好性能, MaOEA-IAR在其余测试问题上获得最好性能, 因此对于翻转的优化问题, PF形状监测基础上的自适应参考点方法依然能发挥较好的作用; WFG1~WFG3分别为混合、断开、退化PF, MaOEA-IAR在大部分测试问题上获得最好性能, 图8描绘了各个算法在15目标WFG1上获得的非支配解的分布情况, 从图中可观察到本文提出的算法在覆盖率和均匀性方面均优于其他算法. 综合统计结果, 在具有不规则PF的测试问题中, 虽然MaOEA-IAR没有在每一个测试问题上获得最好的性能, 但总体性能良好; 这是由于在不规则的PF上, 根据种群的分布生成参考点, 在没有个体分布的区域不设置参考点, 避免在无效区域产生下一代种群.

表 6 MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA以及MaOEA-IAR在DTLZ5~DTLZ7, IDTLZ1~IDTLZ2, WFG1~WFG3上获得IGD值的统一结果(均值和标准差). 最好的结果已被标记

Table 6 The statistical results (mean and standard deviation) of the IGD values obtained by MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA and MaOEA-IAR on DTLZ5~DTLZ7, IDTLZ1~IDTLZ2, WFG1~WFG3. The best results are highlighted

问题	M	MOEA-DD	NSGA-III	RVEA	MOMBI-II	AR-MOEA	MaOEA-IAR
DTLZ5	5	1.0286×10−1 (4.56×10−3)−	1.5564×10−1 (6.36×10−2)−	1.7052×10−1 (2.08×10−2)−	2.6836×10−1 (1.37×10−2)−	1.2293×10−1 (2.95×10−3)−	9.2396×10−2 (1.58×10−2)
	10	1.3275×10−1 (1.77×10−2)+	2.9646×10−1 (9.03×10−2)+	3.7614×10−1 (6.44×10−2)+	5.8454×10−1 (1.64×10−1)−	9.4984×10−2 (3.11×10−3)+	4.8043×10−1 (1.04×10−1)
	15	1.5268×10−1 (4.95×10−3)−	2.5900×10−1 (4.20×10−2)−	5.8957×10−1 (1.74×10−1)−	6.4004×10−1 (6.56×10−2)−	6.0343×10−1 (1.01×10−2)−	1.3313×10−1 (1.25×10−2)
	25	1.4321×10−1 (4.38×10−2)+	8.5001×10−1 (5.98×10−1)−	3.6054×10−1 (2.03×10−1)−	5.7672×10−1 (2.97×10−1)−	9.6898×10−2 (1.91×10−2)−	3.2482×10−2 (1.69×10−1)
DTLZ6	5	1.0630×10−1 (9.13×10−3)+	2.8728×10−1 (2.28×10−1)+	1.5455×10−1 (3.80×10−2)+	3.8061×10−1 (2.25×10−1)=	3.3734×10−1 (3.50×10−2)−	3.1149×10−1 (5.18×10−2)
	10	2.0616×10−1 (1.64×10−1)+	1.5928×10+0 (5.87×10−1)+	2.8394×10−1 (8.30×10−2)+	5.4111×10−1 (2.36×10−1)+	1.6497×10−1 (8.66×10−3)+	2.4129×10+0 (3.39×10−1)
	15	2.0227×10−1 (1.34×10−1)+	2.5854×10+0 (1.02×10+0)=	3.2020×10−1 (1.73×10−1)+	7.5239×10−1 (2.82×10−1)+	1.2810×10−1 (1.01×10−1)+	2.9171×10+0 (4.24×10−1)
	25	1.5709×10−1 (2.14×10−2)−	6.1820×10+0 (3.10×10+0)−	2.2612×10−1 (6.64×10−2)−	5.4816×10−1 (2.83×10−1)−	5.0812×10−1 (3.00×10−1)−	1.0126×10−1 (2.94×10−2)
DTLZ7	5	3.0002×10+0 (9.72×10−4)−	3.3903×10−1 (1.25×10−2)+	6.0021×10−1 (3.12×10−2)−	4.8750×10−1 (8.74×10−2)−	8.7917×10−3 (4.95×10−4)+	4.0035×10−1 (8.59×10−2)
	10	2.0394×10+0 (3.09×10−1)−	1.6480×10+0 (2.43×10−1)−	1.8321×10+0 (4.74×10−1)−	4.8283×10+0 (7.64×10−1)−	2.8392×10−2 (3.28×10−3)+	8.4705×10−1 (3.02×10−2)
	15	3.4630×10+0 (8.21×10−2)−	8.8601×10+0 (7.49×10−1)−	2.3863×10+0 (2.46×10−1)−	1.1222×10+1 (1.43×10−1)−	5.4456×10−1 (3.13×10−1)+	1.6482×10+0 (3.88×10−2)
	25	4.9987×10+0 (4.01×10−2)−	1.4671×10+1 (1.41×10+0)−	3.5010×10+0 (4.87×10−1)+	1.9012×10+1 (2.83×10−1)−	3.7797×10+0 (1.17×10+0)+	4.0533×10+0 (1.41×10−5)
IDTLZ1	5	1.5305×10−1 (4.10×10−2)=	1.3547×10−1 (1.54×10−2)=	1.5234×10−1 (1.70×10−2)=	1.1355×10−1 (3.26×10−4)=	6.5841×10−2 (8.22×10−4)+	2.5128×10−1 (1.65×10−1)
	10	2.2790×10−1 (1.05×10−2)−	1.4175×10−1 (3.27×10−3)−	2.5816×10−1 (2.39×10−2)−	1.8633×10−1 (6.51×10−3)−	1.2386×10−1 (3.42×10−2)=	1.1027×10−1 (9.23×10−4)
	15	3.2984×10−1 (3.09×10−2)−	2.1719×10−1 (4.73×10−3)−	3.5590×10−1 (2.89×10−2)−	2.1098×10−1 (1.14×10−2)−	1.9277×10−1 (1.29×10−2)−	1.7215×10−1 (7.39×10−2)
	25	3.2145×10−1 (1.81×10−2)−	1.9936×10−1 (3.93×10−3)−	3.8507×10−1 (3.13×10−2)−	2.6360×10−1 (6.52×10−3)−	4.3902×10−2 (1.27×10−1)−	2.1252×10−2 (1.63×10−2)
IDTLZ2	5	2.7867×10−1 (5.70×10−3)−	2.4322×10−1 (6.88×10−3)−	2.9833×10−1 (5.13×10−3)−	3.1740×10−1 (1.15×10−3)−	2.1362×10−1 (5.25×10−3)−	2.0888×10−1 (7.30×10−3)
	10	7.3889×10−1 (6.96×10−3)−	6.0395×10−1 (1.69×10−2)−	6.7982×10−1 (7.75×10−3)−	6.6946×10−1 (4.82×10−3)−	4.4639×10−1 (6.90×10−3)−	4.4152×10−1 (6.68×10−3)
	15	9.4524×10−1 (2.03×10−2)−	7.6174×10−1 (1.42×10−2)−	8.7051×10−1 (1.47×10−2)−	8.5834×10−1 (7.35×10−3)−	6.8015×10−1 (1.79×10−2)−	5.7753×10−1 (9.19×10−3)
	25	1.1245×10+0 (1.07×10−2)−	8.3706×10−1 (1.63×10−2)−	1.0678×10+0 (1.60×10−2)−	1.0151×10+0 (4.12×10−3)−	8.9235×10−2 (2.87×10−2)-	2.8098×10−2 (6.87×10−4)
WFG1	5	8.4034×10−1 (1.15×10−1)−	5.6876×10−1 (4.95×10−2)−	5.3556×10−1 (4.24×10−2)−	5.3968×10−1 (6.19×10−2)−	5.1692×10−1 (1.26×10−2)−	4.4951×10−1 (5.18×10−3)
	10	1.2623×10+0 (6.70×10−2)−	1.2030×10+0 (7.30×10−2)−	1.0736×10+0 (6.23×10−2)=	1.2539×10+0 (5.56×10−2)−	1.1573×10+0 (3.43×10−2)−	1.0186×10+0 (3.21×10−2)
	15	1.9032×10+0 (6.34×10−2)−	1.9456×10+0 (8.90×10−2)−	1.8780×10+0 (7.27×10−2)−	2.5378×10+0 (2.18×10−1)−	1.7899×10+0 (4.09×10−2)=	1.7788×10+0 (4.73×10−2)
	25	3.8022×10+0 (5.48×10−2)−	3.0121×10+0 (4.19×10−1)−	3.1303×10+0 (1.12×10−1)−	3.6938×10+0 (9.71×10−2)−	3.1942×10+0 (6.67×10−2)−	2.6916×10+0 (1.82×10−1)
WFG2	5	5.7666×10−1 (1.64×10−2)−	4.6948×10−1 (3.19×10−3)+	4.4930×10−1 (1.01×10−2)+	5.1672×10−1 (6.95×10−2)+	4.7596×10−1 (2.55×10−3)+	5.4316×10−1 (2.97×10−2)
	10	1.4487×10+0 (2.06×10−2)−	1.2010×10+0 (1.43×10−1)−	1.1062×10+0 (3.99×10−2)−	1.6478×10+0 (5.00×10−1)−	1.4937×10+0 (4.68×10−2)−	1.0054×10+0 (1.43×10−2)
	15	2.1614×10+0 (3.30×10−2)−	1.7688×10+0 (7.55×10−2)=	1.7815×10+0 (1.09×10−1)=	7.5478×10+0 (2.36×10+0)−	1.7084×10+0 (3.82×10−2)=	1.7263×10+0 (1.03×10−1)
	25	4.0448×10+0 (1.16×10−2)−	3.5543×10+0 (1.21×10−1)−	2.8225×10+0 (1.52×10−1)−	1.0109×10+1 (5.56×10+0)−	3.1864×10+0 (1.60×10−1)−	2.7976×10+0 (1.71×10−1)
WFG3	5	7.4442×10−1 (3.28×10−2)−	5.9020×10−1 (5.58×10−2)−	6.8641×10−1 (1.11×10−1)−	1.6953×10+0 (1.28×10−1)−	6.8013×10−1 (1.54×10−1)−	5.4840×10−1 (3.21×10−2)
	10	2.7654×10+0 (1.17×10−1)+	1.4175×10+0 (4.13×10−1)+	3.4602×10+0 (5.56×10−1)−	8.5627×10+0 (1.89×10−1)−	2.4166×10+0 (9.05×10−2)+	3.0447×10+0 (5.68×10−1)
	15	6.4307×10+0 (6.67×10−1)+	2.6293×10+0 (4.06×10−1)+	6.6442×10+0 (1.19×10+0)+	1.3900×10+1 (2.03×10−1)−	5.5924×10+0 (2.08×10−1)+	7.5080×10+0 (9.65×10−1)
	25	1.8160×10+1 (3.63×10−2)−	1.2519×10+1 (1.40×10+0)−	1.1530×10+1 (1.65×10+0)−	2.7424×10+1 (3.33×10−2)−	9.8933×10+0 (1.41×10−1)−	6.8891×10+0 (5.11×10+0)
+/−/=		7/24/1	7/22/3	7/22/3	3/27/2	11/18/3
“+”表明该算法优于MaOEA-IAR, “−”劣于MaOEA-IAR, “=”则表示与MaOEA-IAR性能相似

图 7 DTLZ5问题3目标上获得的非支配解

Fig. 7 Nondominated solutions obtained on 3-objective DTLZ5

图 8 WFG1问题15目标上获得的非支配解

Fig. 8 Nondominated solutions obtained on 15-objective WFG1

根据表7的数据分析, 相对于具有规则PF的测试问题, 在不规则PF的测试问题中, 本文提出的算法在多样性方面性能稍逊, 但依然能在大部分问题中保持较好的性能. MOEA-DD在5目标和15目标上的WFG1上获得最好性能; NSGA-III在5目标的DTLZ6, 10目标和25目标的WFG1上以及15目标和25目标的WFG3上获得最好性能; AR-MOEA在5目标的DTLZ5和DTLZ7上获得最好性能; 其余各个目标下的测试问题上, MaOEA-IAR算法获得最好性能. 这在一定程度上证明了利用PF形状自适应参考点能够有效地提升算法的多样性.

表 7 MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA以及MaOEA-IAR在DTLZ5~DTLZ7, IDTLZ1~IDTLZ2, WFG1~WFG3上获得PD值的统一结果(均值和标准差).最好的结果已被标记

Table 7 The statistical results (mean and standard deviation) of the PD values obtained by MOEA-DD、NSGA-III、RVEA、MOMBI-II、AR-MOEA and MaOEA-IAR on DTLZ5~DTLZ7, IDTLZ1~IDTLZ2, WFG1~WFG3. The best results are highlighted

问题	M	MOEA-DD	NSGA-III	RVEA	MOMBI-II	AR-MOEA	MaOEA-IAR
DTLZ5	5	1.7925×10+7 (2.11×10+6)−	3.5995×10+7 (4.18×10+6)+	1.8932×10+7 (4.20×10+6)−	1.1044×10+7 (1.59×10+6)−	4.8118×10+7 (2.34×10+6)+	2.5713×10+7 (2.69×10+6)
	10	1.9742×10+10 (2.54×10+9)−	7.1635×10+10 (5.54×10+9)−	2.9432×10+10 (3.78×10+9)−	2.1484×10+9 (2.81×10+9)−	8.3986×10+10 (3.99×10+9)−	1.2087×10+11 (8.00×10+9)
	15	2.8397×10+11 (7.71×10+10)−	1.1841×10+12 (1.38×10+11)−	4.1423×10+10 (2.81×10+10)−	6.5840×10+9 (4.48×10+9)−	1.0895×10+12 (1.09×10+11)−	2.9251×10+12 (2.88×10+11)
	25	4.2895×10+13 (9.57×10+12)+	1.4562×10+11 (1.05×10+11)−	1.7203×10+13 (1.37×10+13)+	4.0293×10+10 (4.56×10+10)−	1.0108×10+14 (1.23×10+13)−	5.6358×10+14 (2.21×10+14)
DTLZ6	5	2.8362×10+7 (3.50×10+6)−	5.4971×10+7 (7.11×10+6)+	2.6105×10+7 (7.26×10+6)−	1.0490×10+7 (2.67×10+6)−	5.2864×10+7 (3.81×10+6)+	3.1205×10+7 (4.21×10+6)
	10	6.5293×10+10 (1.58×10+10)−	1.8747×10+11 (4.95×10+10)−	5.9078×10+10 (1.80×10+10)−	2.1985×10+9 (2.83×10+9)−	8.4598×10+10 (5.75×10+9)−	3.9921×10+11 (2.70×10+10)
	15	9.1234×10+11 (3.10×10+11)−	3.4359×10+12 (5.79×10+11)−	7.4856×10+11 (3.95×10+11)−	1.0372×10+10 (1.40×10+10)−	4.2785×10+11 (3.48×10+11)−	7.9758×10+12 (8.70×10+11)
	25	2.2080×10+14 (1.01×10+14)−	2.2455×10+14 (1.56×10+13)−	8.7904×10+13 (2.72×10+13)−	1.5169×10+11 (1.15×10+11)−	3.2540×10+13 (1.77×10+13)−	2.3216×10+15 (1.08×10+15)
DTLZ7	5	1.6766×10+3 (4.84×10+3)−	2.1762×10+7 (4.10×10+6)=	1.8563×10+7 (3.07×10+6)=	5.1253×10+6 (7.63×10+5)−	3.3243×10+7 (4.17×10+6)+	2.0833×10+7 (7.02×10+6)
	10	2.1457×10+9 (1.38×10+9)−	3.1794×10+10 (2.69×10+9)−	1.6034×10+10 (4.07×10+9)−	8.0445×10+9 (1.73×10+9)−	2.5524×10+10 (3.65×10+9)−	6.8683×10+10 (7.18×10+9)
	15	1.8990×10+10 (5.95×10+9)−	4.7550×10+11 (9.43×10+10)−	2.7698×10+11 (6.40×10+10)−	4.9554×10+10 (2.76×10+10)−	4.0328×10+11 (1.19×10+11)−	2.5059×10+12 (3.10×10+11)
	25	4.2556×10+12 (1.02×10+12)−	7.3834×10+13 (1.20×10+13)−	4.7217×10+13 (1.00×10+13)−	4.4333×10+13 (1.34×10+13)−	1.3427×10+9 (6.62×10+8)−	1.1453×10+14 (1.61×10+13)
IDTLZ1	5	1.4745×10+6 (9.43×10+5)−	6.3366×10+6 (3.40×10+6)−	2.1610×10+6 (9.83×10+5)−	8.4010×10+5 (2.39×10+5)−	1.0739×10+7 (2.67×10+6)−	1.9799×10+8 (2.32×10+8)
	10	1.0063×10+8 (1.13×10+8)−	9.8146×10+9 (1.30×10+9)−	1.0241×10+9 (9.00×10+8)−	2.0726×10+9 (3.55×10+8)−	7.1952×10+9 (1.15×10+9)−	4.5218×10+10 (1.18×10+11)
	15	4.8749×10+10 (2.39×10+11)−	2.7098×10+11 (4.55×10+10)−	6.2342×10+10 (5.79×10+10)−	3.9405×10+10 (8.72×10+9)−	1.2277×10+11 (3.42×10+11)−	3.2538×10+12 (1.06×10+13)
	25	3.8837×10+9 (8.47×10+9)−	5.6426×10+13 (1.28×10+13)−	7.6673×10+12 (5.54×10+12)−	1.6889×10+12 (1.19×10+12)−	1.6465×10+14 (4.61×10+14)−	5.8266×10+14 (1.42×10+13)
IDTLZ2	5	1.2432×10+7 (1.92×10+6)−	3.5278×10+7 (7.22×10+6)−	1.8123×10+7 (1.50×10+6)−	4.8079×10+6 (6.93×10+5)−	2.6241×10+7 (1.72×10+6)−	5.5348×10+7 (2.41×10+6)
	10	3.7649×10+9 (3.38×10+8)−	4.9622×10+10 (7.67×10+9)−	1.1533×10+10 (1.30×10+9)−	1.5701×10+10 (1.85×10+9)−	9.1979×10+10 (3.71×10+9)−	1.6089×10+11 (4.17×10+9)
	15	7.1923×10+10 (3.07×10+10)−	1.0779×10+12 (1.50×10+11)−	2.0643×10+11 (6.01×10+10)−	2.9274×10+11 (4.07×10+10)−	2.6072×10+12 (1.61×10+11)−	5.4279×10+12 (1.82×10+11)
	25	4.4848×10+12 (1.99×10+12)−	5.6171×10+14 (8.35×10+13)−	1.4306×10+13 (8.54×10+12)−	7.0067×10+13 (1.05×10+13)−	8.5860×10+14 (4.94×10+13)−	2.0550×10+15 (5.47×10+13)
WFG1	5	7.7570×10+7 (4.76×10+6)+	7.5733×10+7 (7.14×10+6)+	6.6169×10+7 (5.02×10+6)+	7.6250×10+6 (2.77×10+6)−	3.0367×10+7 (2.17×10+6)+	2.3345×10+7 (3.37×10+6)
	10	3.8144×10+10 (3.75×10+9)+	8.4159×10+10 (8.64×10+9)+	4.6067×10+10 (6.62×10+9)+	6.4761×10+9 (1.55×10+9)−	4.3604×10+10 (2.26×10+9)+	1.8476×10+10 (2.80×10+9)
	15	1.3448×10+12 (2.24×10+11)+	1.2676×10+12 (5.92×10+11)+	6.2449×10+11 (1.04×10+11)=	1.9369×10+10 (2.14×10+10)−	6.0993×10+11 (4.26×10+10)=	6.1772×10+11 (1.26×10+11)
	25	3.3402×10+13 (2.45×10+12)−	1.6094×10+14 (4.13×10+13)+	1.0889×10+14 (5.98×10+12)+	4.8564×10+12 (1.42×10+12)−	1.0664×10+14 (3.18×10+12)+	8.4524×10+13 (1.67×10+13)
WFG2	5	5.1237×10+7 (2.65×10+6)−	5.4016×10+7 (3.16×10+6)−	6.1875×10+7 (2.87×10+6)−	1.1742×10+7 (3.17×10+6)−	3.8312×10+7 (2.55×10+6)−	7.6371×10+7 (4.16×10+6)
	10	3.9168×10+10 (1.43×10+9)−	6.6429×10+10 (1.01×10+10)−	5.3106×10+10 (2.41×10+9)−	7.4067×10+9 (5.52×10+9)−	3.9309×10+10 (2.97×10+9)−	9.1141×10+10 (4.59×10+9)
	15	4.4512×10+11 (4.65×10+10)−	1.5952×10+12 (2.02×10+11)−	9.2321×10+11 (1.58×10+11)−	1.2053×10+10 (1.52×10+10)−	5.7677×10+11 (8.49×10+10)−	2.2461×10+12 (1.65×10+11)
	25	4.1805×10+13 (3.61×10+12)−	3.8842×10+14 (1.07×10+14)−	1.7542×10+14 (2.40×10+13)−	3.8888×10+11 (9.15×10+11)−	1.6560×10+14 (1.30×10+13)−	4.7295×10+14 (2.67×10+13)
WFG3	5	1.2116×10+8 (9.07×10+6)−	1.4756×10+8 (7.56×10+6)−	1.3033×10+8 (1.40×10+7)−	5.1396×10+7 (4.21×10+6)−	1.5433×10+8 (7.28×10+6)=	1.5501×10+8 (6.95×10+6)
	10	1.1096×10+11 (9.29×10+9)−	2.4982×10+11 (2.39×10+10)−	1.6581×10+11 (1.63×10+10)−	9.4558×10+8 (1.51×10+8)−	1.9220×10+11 (1.05×10+10)−	3.1718×10+11 (2.00×10+10)
	15	3.8028×10+12 (7.77×10+11)−	7.4227×10+12 (1.37×10+12)+	4.1520×10+12 (7.83×10+11)−	1.6200×10+10 (5.00×10+9)−	2.7152×10+12 (9.23×10+11)−	6.1382×10+12 (5.23×10+11)
	25	1.0941×10+14 (6.89×10+12)−	1.9873×10+15 (6.87×10+14)=	5.6632×10+14 (1.69×10+14)−	5.1563×10+10 (1.66×10+10)−	3.2575×10+14 (2.26×10+13)−	1.5572×10+15 (1.06×10+14)
+/−/=		4/28/0	7/23/2	4/26/2	0/32/0	6/24/2
“+”表明该算法优于MaOEA-IAR, “−”劣于MaOEA-IAR, “=”则表示与MaOEA-IAR性能相似

3.4 算法的运行时间分析

为了增加实验结果的说服力, 对算法的运行时间进行对比. 由于参考点自适应策略较为耗费时间, 与传统算法进行时间上的对比无太大意义, 因此本节将同样利用参考点自适应策略的算法AR-MOEA与MaOEA-IAR进行对比. 从表8中可以观察到, MaOEA-IAR在大部分的测试问题中能在较短的时间内完成种群的进化, 即在更短的时间内得到质量更好的种群, 算法的性能较为优越.

表 8 AR-MOEA和MaOEA-IAR在DTLZ1~DTLZ7, IDTLZ1~IDTLZ2, WFG1~WFG9上运行时间的统一结果(均值). 最好的结果已被标记

Table 8 The statistical results (mean) of the time obtained by AR-MOEA and MaOEA-IAR on DTLZ1~DTLZ7, IDTLZ1~IDTLZ2, WFG1~WFG9. The best results are highlighted

问题	M	AR-MOEA	MaOEA-IAR	问题	M	AR-MOEA	MaOEA-IAR
DTLZ1	5	8.7284×10+1−	5.2877×10+1	WFG1	5	2.1497×10+2−	1.2453×10+2
	10	3.2368×10+3−	1.4929×10+3		10	3.0802×10+3−	1.8838×10+3
	15	1.5646×10+2+	4.5986×10+2		15	3.3103×10+2−	2.9192×10+2
	25	2.7908×10+3−	1.8621×10+3		25	2.4172×10+3+	2.8807×10+3
DTLZ2	5	1.4045×10+2+	3.1151×10+2	WFG2	5	2.5691×10+2−	1.9505×10+2
	10	3.4692×10+3−	2.0823×10+3		10	3.6336×10+3−	3.2122×10+3
	15	1.9603×10+2+	4.9719×10+2		15	4.3556×10+2−	3.8969×10+2
	25	3.1545×10+3+	3.4599×10+3		25	3.4466×10+3=	3.3881×10+3
DTLZ3	5	7.6826×10+1−	3.3370×10+1	WFG3	5	3.4018×10+2−	3.2435×10+2
	10	3.2959×10+3−	1.5038×10+3		10	4.3267×10+3−	4.1139×10+3
	15	4.9418×10+2−	1.5822×10+2		15	5.1973×10+2−	4.3731×10+2
	25	2.9858×10+3−	1.7848×10+3		25	3.8047×10+3=	3.7357×10+3
DTLZ4	5	1.4659×10+2+	3.2766×10+2	WFG4	5	3.3620×10+2−	2.8286×10+2
	10	3.8768×10+3−	2.1238×10+3		10	4.2819×10+3−	3.6326×10+3
	15	1.9815×10+2+	5.1050×10+2		15	3.8595×10+2+	5.2267×10+2
	25	3.1269×10+3+	3.2684×10+3		25	3.7546×10+3−	3.3598×10+3
DTLZ5	5	2.2500×10+2−	1.3912×10+2	WFG5	5	3.3378×10+2−	2.9287×10+2
	10	3.0904×10+3−	1.9358×10+3		10	4.2697×10+3−	3.7511×10+3
	15	1.8227×10+2+	4.5443×10+2		15	5.2633×10+2−	4.0438×10+2
	25	3.0757×10+3−	1.9646×10+3		25	3.8177×10+3−	3.4843×10+3
DTLZ6	5	1.9591×10+2−	1.2208×10+2	WFG6	5	2.7412×10+2−	2.5095×10+2
	10	3.5852×10+3−	1.8312×10+3		10	4.0843×10+3−	3.2581×10+3
	15	1.5310×10+2+	4.9933×10+2		15	3.1397×10+2+	5.1200×10+2
	25	2.6990×10+3−	2.0808×10+3		25	3.7598×10+3−	2.8335×10+3
DTLZ7	5	2.0799×10+2−	1.4207×10+2	WFG7	5	3.7091×10+2−	3.1761×10+2
	10	3.8714×10+3−	2.3062×10+3		10	4.3950×10+3−	3.7082×10+3
	15	4.8328×10+2−	2.0122×10+2		15	3.7417×10+2+	5.2910×10+2
	25	2.4555×10+3−	1.5033×10+3		25	3.8242×10+3−	3.2364×10+3
IDTLZ1	5	2.1931×10+2−	9.4000×10+1	WFG8	5	2.2219×10+2=	2.1770×10+2
	10	3.1281×10+3−	1.9947×10+3		10	3.7129×10+3−	2.6444×10+3
	15	3.4287×10+2−	2.5752×10+2		15	2.4552×10+2+	4.5493×10+2
	25	2.0253×10+3−	1.2549×10+3		25	3.7527×10+3−	2.5151×10+3
IDTLZ2	5	3.1594×10+2+	3.3723×10+2	WFG9	5	3.8469×10+2−	3.2047×10+2
	10	4.0353×10+3−	3.4738×10+3		10	4.3729×10+3−	3.9448×10+3
	15	4.4610×10+2−	4.2203×10+2		15	5.3114×10+2−	4.3118×10+2
	25	2.5265×10+3−	1.7758×10+3		25	3.8142×10+3−	3.5823×10+3
+/−/=		10/26/0		+/−/=		5/28/3
“+”表明该算法优于MaOEA-IAR, “−”劣于MaOEA-IAR, “=”则表示与MaOEA-IAR性能相似

3.5 参考点自适应策略的有效性分析

在本节中, 为了验证参考点自适应策略的有效性, 对比AR-MOEA与MaOEA-IAR在测试问题MaF1~MaF7上的性能. AR-MOEA与MaOEA-IAR都采用了参考点自适应策略增加参考点的多样性, 并且在环境选择中都利用IGD-NS指标计算适应度值并将其作为选择标准; MaF测试集中包含更多类型的优化问题, 并且增加了具有凹型PF的优化问题, 这一类优化问题对生成参考点的策略要求更高. 表9为算法独立运行30次的IGD指标值, 其余设置与上述实验设置相同. 从表中的数据可以观察到MaOEA-IAR在10目标的MaF6和5目标的MaF7上未能获得最好性能, 在其余测试问题上获得最好性能, 算法中使用到的参考点自适应策略适用于各种形状的优化问题.

表 9 AR-MOEA和MaOEA-IAR在MaF1~MaF7上获得IGD值的统一结果(均值和标准差). 最好的结果已被标记

Table 9 The statistical results (mean and standard deviation) of the IGD values obtained by AR-MOEA and MaOEA-IAR on MaF1~MaF7. The best results are highlighted

问题	M	AR-MOEA	MaOEA-IAR
MaF1	5	6.1773×10−2 (6.75×10−2)−	3.2287×10−3 (7.05×10−5)
	10	1.0257×10−1 (1.11×10−1)−	6.5011×10−3 (1.44×10−4)
	15	1.6987×10−1 (1.85×10−1)−	1.1253×10−2 (2.95×10−4)
	25	1.7434×10−1 (1.89×10−1)−	9.2626×10−3 (1.97×10−4)
MaF2	5	5.6263×10−2 (5.26×10−2)−	8.5071×10−3 (3.31×10−4)
	10	8.3280×10−2 (8.77×10−2)−	6.4968×10−3 (9.61×10−5)
	15	1.2184×10−1 (1.24×10−1)−	8.9506×10−3 (2.26×10−4)
	25	1.0515×10−1 (1.21×10−1)−	6.2938×10−3 (4.48×10−4)
MaF3	5	3.4660×10−2 (4.22×10−2)−	1.0505×10−3 (8.53×10−4)
	10	3.4304×10−2 (4.06×10−2)−	4.8646×10−3 (8.72×10−3)
	15	1.6992×10+0 (6.87×10+0)−	3.9708×10−3 (3.15×10−3)
	25	8.5024×10−1 (2.47×10+0)−	2.0315×10−3 (2.00×10−3)
MaF4	5	1.0234×10+0 (1.26×10+0)−	4.5541×10−2 (9.87×10−3)
	10	3.6718×10+1 (4.35×10+1)−	1.7669×10+0 (1.34×10−2)
	15	1.7572×10+3 (2.01×10+3)−	2.7158×10+2 (5.78×10−1)
	25	1.8804×10+6 (2.17×10+6)−	1.7062×10+5 (3.15×10+2)
MaF5	5	1.0214×10+0 (1.29×10+0)−	6.3123×10−2 (1.23×10−2)
	10	3.7332×10+1 (4.78×10+1)−	6.3090×10−1 (9.64×10−2)
	15	1.4852×10+3 (1.90×10+3)−	3.6171×10+0 (1.29×10+0)
	25	1.7966×10+6 (2.32×10+6)−	7.1131×10+0 (8.87×10+0)
MaF6	5	1.3381×10−3 (1.72×10−3)−	4.2532×10−6 (1.43×10−6)
	10	3.1054×10−1 (1.30×10+0)+	4.8255×10+0 (3.33×10+0)
	15	2.1990×10−1 (7.89×10−1)−	4.6076×10−6 (1.37×10−6)
	25	3.5425×10−1 (5.51×10−1)−	3.7808×10−6 (4.08×10−6)
MaF7	5	1.3383×10−1 (1.61×10−1)=	1.8586×10−1 (2.35×10−1)
	10	5.7112×10−1 (6.97×10−1)=	3.5443×10−1 (4.13×10−1)
	15	2.2371×10+0 (2.25×10+0)−	7.1977×10−1 (7.75×10−1)
	25	3.6581×10+0 (3.86×10+0)−	1.1867×10−1 (8.44×10−1)
+/−/=		1/25/2
“+”表明该算法优于MaOEA-IAR, “−”劣于MaOEA-IAR, “=”则表示与MaOEA-IAR性能相似

3.6 邻域参数r的分析和讨论

邻域参数在算法中起着重要作用, 但由于该参数为用户预先定义参数, 虽然在参考点自适应策略中描述了如何调整参数, 其初始值却较难确定; 因此在本节将算法中的邻域参数r的初始值分别设置为5, 7, 9, 11, 13, 对比不同取值下算法在测试问题DTLZ1、DTLZ5、IDTLZ1、WFG1、WFG2、WFG4上获得的IGD指标值. 从表10中可观察到在大部分的目标下, 当r取值为9时能获得最好的指标值; 在25目标的DTLZ1和10目标、25目标的WFG4上, 虽然算法在r为11时获得最好性能, 但r为9时的性能与最好性能相似; 因此, 将9作为邻域参数r的初始值.

表 10 不同参数下算法MaOEA-IAR的性能

Table 10 Performance of MaOEA-IAR under different parameters

问题	目标数	r初始值
问题	目标数	5	7	9	11	13
DTLZ1	5	2.6870×10−1	2.6135×10−1	2.6051×10−1	2.6382×10−1	2.6351×10−1
	10	4.8177×10+1	4.7009×10+1	4.6085×10+1	4.7519×10+1	4.7286×10+1
	15	5.7026×10+1	5.6981×10+1	5.5765×10+1	5.6146×10+1	5.6083×10+1
	25	4.5156×10−1	4.5013×10−1	3.6557×10−1	2.4067×10−1	2.4052×10−1
DTLZ5	5	9.2396×10−2	8.3615×10−2	8.0045×10−2	8.8463×10−2	8.8732×10−2
	10	6.2597×10−1	4.7625×10−1	4.7044×10−1	4.7765×10−1	4.7829×10−1
	15	1.3549×10−1	1.3158×10−1	1.2994×10−1	1.3036×10−1	1.3023×10−1
	25	3.3464×10−2	3.3391×10−2	3.3301×10−2	3.3362×10−2	3.3485×10−2
IDTLZ1	5	2.5128×10−1	2.3743×10−1	2.1694×10−1	2.2748×10−1	2.2926×10−1
	10	1.1236×10−1	1.1149×10−1	1.0017×10−1	1.0594×10−1	1.0542×10−1
	15	1.8035×10−1	1.7891×10−1	1.7077×10−1	1.7901×10−1	1.7924×10−1
	25	2.2693×10−2	2.2451×10−2	2.2279×10−2	2.2538×10−2	2.2523×10−2
WFG1	5	4.4951×10−1	4.3826×10−1	4.3007×10−1	4.3596×10−1	4.4001×10−1
	10	1.1967×10+0	1.1051×10+0	1.0186×10+0	1.0598×10+0	1.0482×10+0
	15	1.6956×10+0	1.5941×10+0	1.5076×10+0	1.6582×10+0	1.6677×10+0
	25	2.8015×10+0	2.7693×10+0	2.6724×10+0	2.7795×10+0	2.7619×10+0
WFG2	5	5.4316×10−1	5.4029×10−1	5.4002×10−1	5.4174×10−1	5.4169×10−1
	10	1.1086×10+0	1.0997×10+0	1.0051×10+0	1.1036×10+0	1.1097×10+0
	15	1.8675×10+0	1.7649×10+0	1.7069×10+0	1.8007×10+0	1.7952×10+0
	25	2.9598×10+0	2.9413×10+0	2.8039×10+0	2.8796×10+0	2.8976×10+0
WFG4	5	1.1192×10+0	1.1128×10+0	1.1065×10+0	1.1097×10+0	1.1106×10+0
	10	4.1062×10+0	4.1057×10+0	4.0388×10+0	4.0263×10+0	4.0589×10+0
	15	8.9645×10+0	8.8089×10+0	8.3986×10+0	8.4108×10+0	8.4004×10+0
	25	1.9058×10+1	1.8769×10+1	1.6506×10+1	1.5375×10+1	1.6405×10+1

4. 总结

为了改善参考点的适应能力, 提高算法在处理具有不同PF形状的优化问题上的通用性, 本文提出参考点自适应调整下评价指标驱动的高维多目标进化算法(MaOEA-IAR), 该算法设计一个PF形状监测基础上的自适应参考点方法, 通过种群分布状态以轮廓曲线近似PF, 结合曲线参数生成一组多样性好的参考点; 同时在匹配选择中利用Pareto支配以及改进的Pareto支配选择一组有希望的父代种群; 两者结合共同指导种群进化.

实验证明本文提出的算法在处理各种PF的MaOPs时能获得较好的性能, 同时在增强种群多样性方面效果明显; 然而在判断PF形状时, 由于某些测试问题不是纯粹的线性、凹型或凸型, 因此对于这样的测试问题可能会出现PF形状判断错误的情况, 这在一定程度上对结果造成偏差, 因此下一步的工作计划是继续优化判断PF形状的方法, 增强算法在处理复杂PF问题时的性能.

关键字：优秀论文

上一篇：基于改进YOLOv3算法的公路车道线检测方法
下一篇：产地、年份、品种对葡萄干矿物元素含量的影响

栏目分类

热门排行

推荐信息

期刊知识