微纳多孔结构中稀薄气体流动渗透率的解析型预测模型

作者：杨光程鑫王峥王晔张良俊吴静怡来源：《化工学报》日期：2022-10-28人气：2287

多孔结构中的稀薄气体流动机理在石油化工、能源利用、航空航天等领域具有广阔的应用前景[1-3]，如航天推进剂的增压输送、非常规油气开采、质子交换膜燃料电池、CO2封存、核废料处理等。近年来，3D打印、MEMS技术的发展也推动着对微纳尺度气体流动特性的深入研究[4-5]。当多孔结构的孔隙尺度足够小，或者气体工质处于低压状态时，气体分子的平均自由程与孔隙的特征长度相当，气体分子与固体壁面的碰撞频率和气体分子间的碰撞频率相近，即产生稀薄气体效应。该现象通常用Knudsen数（Kn）来量化，它表征了气体分子平均自由程（λ）与流动特征长度（Lc）的比值，并可将气体的流动大致分为四种状态：连续流（Kn≤0.001），滑移流（0.001<Kn≤0.1），过渡流（0.1<Kn≤10）和自由分子流（Kn>10）。对于非连续区的高Kn流动，壁面流动速度的“无滑移”假设不再成立，从而导致气体的表观渗透率高于材料的固体渗透率，这种现象也被称为Klinkenberg效应。而目前常用的多孔结构渗透率模型，如Carman-Kozeny模型、Rumpf-Gupte模型等均未考虑气体稀薄效应的影响。

Klinkenberg[6]提出了多孔结构中稀薄气体表观渗透率的表达式Ka=K∞(1+n/p)。其中，K∞为材料的固有渗透率，只与多孔材料本身的几何特征有关；n为修正因子，取决于孔隙尺度的流动形态，也可以表示为Kn的函数。在过去的几十年中，国内外学者在上述表达式的基础上提出了更多形式的表观渗透率关联式[7-13]，以适用于具有复杂孔隙形式的多孔结构以及高压等复杂条件。然而，现有稀薄气体流动渗透率的关联式大多为半解析型或经验型，其模型参数通过数值模拟或实验数据拟合的方式获得。此外，由于在不同应用中的多孔结构形式多样、孔隙的几何拓扑复杂，不同关联式通常只适用于特定形式的多孔结构。随着微纳制造技术的发展，使得具有有序性孔隙的微纳多孔结构得以工程化应用[14-19]。由于其孔隙的三维拓扑结构具有精确的数学描述，为从孔隙尺度流动机理层面上获得表观渗透率的解析型模型提供了可能。

本文从多孔结构孔隙尺度的流动机理出发，确定了多孔结构固有渗透率、孔隙率、弯曲度、收缩-扩张因子和有效孔隙尺寸之间的定量关系。并以此为基础，定义一种新的多孔结构有效孔隙尺寸。该有效孔隙尺寸可以完全利用多孔结构的几何参数进行确定，不依赖于仿真或实验数据的输入。通过将该有效孔隙尺寸与稀薄气体管道流动模型相结合，推导出一种具有通用性的稀薄气体表观渗透率模型。基于高精度的直接模拟Monte Carlo方法（direct simulation Monte Carlo, DSMC）对不同工况下的流动状态进行数值模拟分析，对所提模型的准确性进行验证。

1 理论分析

1.1 多孔结构固有渗透率表达式

固有渗透率，也称为绝对渗透率，反映了多孔材料本身的属性，其值为满足Darcy定律条件时的单相流动渗透率。忽略多孔结构中的闭合孔隙，当孔隙空间Ω中充满不可压缩的低Reynolds数（Re<1）牛顿流体时，孔隙中的稳态流动可由Stokes方程和连续性方程控制：

$μ \nabla^{2} u = \nabla p$ （1） $\nabla ∙ u = 0$ （2）

假设多孔结构孔隙中的任何一点都隶属于某条连通了多孔区域入口和出口的流线S。令Ω表示所有流线所占据空间的集合，则孔隙率可定义为Ω和多孔介质总体积V的比值，即

$ε = \frac{Ω}{V}$ （3）

多孔介质中牛顿流体的缓慢流动特性可以由Darcy定律描述

$K_{\infty} = - \frac{Q μ L}{A Δ p}$ （4）

式中，Q为流体的流量；A为多孔介质截面积；L为多孔区域长度； $Δ$ p为流过多孔区域的前后压差。Darcy定律也可写成沿流体区域的积分形式：

$K_{\infty} = - \frac{Q μ L}{A Δ p} = ε \frac{1}{Ω} \int_{Ω}^{} - μ \nabla p ∙ u {(\frac{L}{Δ p})}^{2} d V$ （5）

定义微元的渗透率因子 $k$ ：

$k = \frac{K_{\infty}}{ε} = \frac{1}{Ω} \int_{Ω}^{} - μ \nabla p ∙ u {(\frac{L}{Δ p})}^{2} d V$ （6）

按照前面的假设，将孔隙空间Ω离散为无数个流线S的集合，并定义单条流线上的渗透率因子：

$k (S) = - \frac{μ L^{2}}{Δ p}$ （7）

结合式（6）、式（7），可以得出[20]

$k = \frac{1}{Ω} \int_{Â}^{} k (S) d Q_{S} = \frac{k (S)}{Ω} \int_{Â}^{} d Q_{S} = \frac{Q}{Ω} k (S)$ （8）

式中，Â为两个标量函数x和y构成的二维面域。由于多孔结构孔隙中的流线特征与孔隙弯曲度和收缩-扩张特性有关。下面分别对其进行定义。

孔隙的弯曲度可定义为多孔介质长度L和实际流线长度Ls的比值[图1(a)]：

$τ (S) = \frac{L}{L_{s}}$ （9）

图1

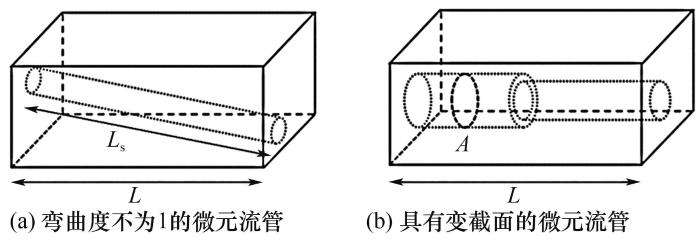
图1 理想多孔介质中的微元流管

Fig.1 Micro-element flow tube in idealized porous media

其值越小代表孔隙的弯曲程度越大（也有文献中采用相反比值的定义）。

对于变截面流动通道[图1(b)]，通道长度为L，通道长度方向位置x处的流动截面积为 $A (x)$ ，其截面的收缩-扩张因子可以描述为：

$C = \frac{1}{L^{2}} \int_{0}^{L} A {(x)}^{2} d x \int_{0}^{L} \frac{1}{A {(x)}^{2}} d x$ （10）

根据面积与压差的关系[21]，进一步可得

$C = \frac{1}{L^{2}} \int_{0}^{L} \frac{1}{\nabla p (x)} d x \int_{0}^{L} \nabla p (x) d x$ （11）

将上式应用于流线S上，并利用沿流线的压力梯度 $\frac{δ p}{δ S} = \frac{\nabla p ∙ u}{u}$ 替换式（11）中的压力梯度，可得到流线上的收缩-扩张因子表达式：

$C (S) = \frac{1}{L_{s}^{2}} \int_{S}^{} \frac{u}{\nabla p ∙ u} d S \int_{S}^{} \frac{\nabla p ∙ u}{u} d S = \frac{1}{L_{s}^{2}} Δ p \int_{S}^{} \frac{u}{\nabla p ∙ u} d S$ （12）

根据水力传导系数的定义[22]：

$B = - \frac{μ u^{2}}{\nabla p ∙ u}$ （13）

则单条流线上的水力传导系数为：

$B (S) = \int_{S}^{} B \frac{1}{u} d S = \int_{S}^{} - \frac{μ u}{\nabla p ∙ u} d S$ （14）

结合式（7）、式（9）、式（12）、式（14），可得，在单条流线上满足如下关系式：

$k (S) = \frac{B (S) τ {(S)}^{2}}{C (S)}$ （15）

将式（15）中的各变量在孔隙空间Ω内进行体积积分，并结合式（6）可得

$K_{\infty} = \frac{τ^{2} B ε}{C}$ （16）

式（16）给出了固有渗透率、水力传导系数、孔隙率、孔隙弯曲度和收缩-扩张因子之间的定量关系。

结合式（5）和式（16）可以得出，对于平直圆管中的流动

$K_{\infty} = - \frac{Q μ L}{A Δ p} = B$ （17）

另外，平直圆管流动可以利用Hagen-Poisseuille方程来描述

$Q = - \frac{π R^{4} Δ p}{8 μ L}$ （18）

式中，R为圆管的管道半径。结合式（17）和式（18）可以得出管道半径 $R = \sqrt[]{8 B}$ 。因此，通过上述类比，对于由复杂孔隙组成的多孔结构，可将表征孔隙有效尺寸的特征半径取 $R_{c} = \sqrt[]{8 B}$ ，并结合式（16），即

$R_{c} = \sqrt[]{\frac{8 K_{\infty} C}{τ^{2} ε}}$ （19）

由于 $K_{\infty}$ 、C、 $τ$ 和 $ε$ 均只与多孔结构孔隙的几何信息有关，按照式（18）定义的Rc也只取决于多孔结构的几何特性。

1.2 多孔结构中的稀薄气体渗透率模型

气体的稀薄程度可以用Knudsen数来表示，对于平直圆管流动：

$K n = \frac{λ}{R}$ （20）

式中，λ为气体分子平均自由程。根据Bird[23]提出的可变硬球模型（variable hard sphere, VHS），实际气体的平均分子自由程可以表示为：

$λ = \frac{2 (5 - 2 ω) (7 - 2 ω)}{15} {(\frac{m}{2 π b T})}^{\frac{1}{2}} \frac{μ}{ρ}$ （21）

式中，μ为气体动力黏度；ρ为气体密度；m为气体分子质量；b为Boltzmann常数，取值1.38×10-23； $ω$ 为温度系数，反映了黏度与温度间的关系。

早在1909年，Knudsen发现随着平均压力降低气体密度减小，在给定压降下通过毛细管的气体质量流量会先减小后增大，并提出了如下公式来计算高Knudsen数下的气体流量[24]：

$\frac{K_{a}}{K_{\infty}} = 1 + \frac{64}{3 π} \times \frac{1 + c_{1}^{K} p}{1 + c_{2}^{K} p} K n$ （22） $c_{1}^{K} p = \sqrt[]{\frac{π}{2}} \times \frac{2}{K n}, c_{2}^{K} p = \sqrt[]{\frac{π}{2}} \times \frac{2.47}{K n}$ （23）

对于实际多孔材料，由于孔隙几何特征的复杂性，特征长度不能通过直径或半径来直接获得。由于从本质上来讲，Knudsen数的分母中的特征长度为气体分子与固体分子间的平均碰撞距离，可按照式（19）的定义对其进行确定。因此，可将式（20）、式（22）、式（23）进一步写为

$K n_{p} = \frac{λ τ \sqrt[]{ε}}{\sqrt[]{8 K_{\infty} C}}$ （24） $\frac{K_{a}}{K_{\infty}} = 1 + \frac{64}{3 π} \times \frac{1 + c_{1}^{K} p}{1 + c_{2}^{K} p} K n_{p}$ （25） $c_{1}^{K} p = \sqrt[]{\frac{π}{2}} \times \frac{2}{K n_{p}}, c_{2}^{K} p = \sqrt[]{\frac{π}{2}} \times \frac{2.47}{K n_{p}}$ （26）

因此，根据式(21)、式(24)~式(26)，可以在孔隙几何结构和气体的状态参数已知的情况下，对多孔结构中稀薄气体的表观渗透率进行预测计算。

2 DSMC模拟验证

2.1 数学模型

为了验证本文所提出的表观渗透率模型的准确性，基于直接模拟Monte Carlo方法（DSMC）开展了不同条件下的多孔结构稀薄气体流动特性仿真。DSMC是一种基于粒子运动的模拟方法，并收敛于Boltzmann方程[25]，因此可以对稀薄状态下的气体流动过程进行精确模拟。DSMC的模拟精度已通过不同Kn区间的实验数据所验证[26]。其在特定问题上的模拟精度高于格子Boltzmann方法，效率高于分子动力学模拟。本文的DSMC代码已在基于C++的开源平台OpenFOAM上实现（dsmcFoam）[27]。流体区域中的计算网格尺寸设置为气体最小平均自由程的1/3，计算时间步长设置为分子的平均碰撞时间的1/5。为了减少统计误差和提高模拟精度，每个计算单元内设置不少于10个粒子[28]。采用无时间计数器（no time counter, NTC）方法选择碰撞对，采用可变硬球模型（VHS）和Larsen-Borgnkke内能重分布模型模拟粒子间的碰撞行为。DSMC模拟的典型步骤包括：（1）将计算粒子索引到计算单元；（2）计算追踪粒子的运动；（3）进行碰撞并计算碰撞后的状态。重复这些流程直到宏观变量的统计误差足够小。最后通过对每个单元的粒子特性进行统计采样和平均化处理，得到压力、密度、速度、温度等宏观参数[29]。本文所采用的DSMC方法已在作者前期的研究中得到验证[29]。

2.2 物理模型与流动特性

在本文的验证性模拟中，采用了三种形式的孔隙结构。如图2所示，组成多孔结构的固体微元分别设置为三维立方体[图2（a）]、二维圆形[图2（b）]和二维矩形[图2（c）]。沿x方向设置压力入口和压力出口，y（z）方向采用周期性边界条件。气体入口温度和固体微元表面温度均恒定为273 K。固体微元的尺寸区间范围为20~400 nm。通过改变微元间距，调节孔隙率范围为0.12≤ε≤0.90。分别以氩气（Ar）、氦气（He）、氮气（N2）和甲烷（CH4）为流动工质，其物性如表1所示。此外，图2也给出了在Knp =1时不同形式的多孔结构孔隙中的速度分布云图，不同结构内的气体速度沿流动方向均逐渐增大，这是因为随着气流向出口发展，局部压力减小，导致气体密度也逐渐减小。

图2

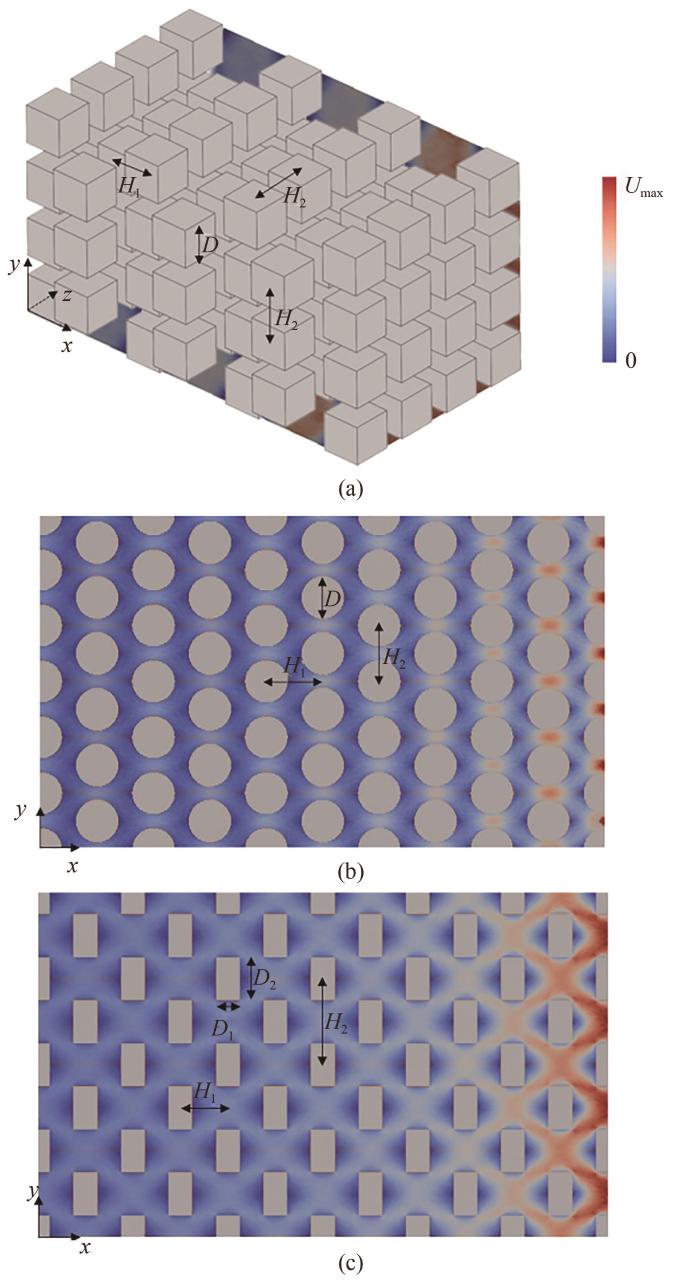
图2 多孔结构的物理模型及在Knp =1条件下的典型流场分布

Fig.2 Physical modes of the porous structures and flow fields at Knp =1

表1 气体工质物性［23］

Table 1 Physical properties of gas species［23］

气体种类	分子直径(d)/ 10-10 m	分子质量(m)/ 10-23 kg	自由度(ξ)	温度系数(ω)
氩气 (Ar)	4.17	66.3	3	0.81
氦气 (He)	2.33	6.65	3	0.66
甲烷 (CH4)	4.83	26.6	6.4	0.84
氮气 (N2)	4.17	46.5	5	0.74

新窗口打开| 下载CSV

2.3 多孔结构中的稀薄气体渗透率特性

图3（a）为在固体微元为矩形[图2（c）]，D1=D2=100 nm，孔隙率ε=0.75，入口压力0.25 MPa，出口压力0.05 MPa条件下，采用不同气体工质时多孔结构中心线（y=0）上的速度分布。在该边界条件下，氦气分子的平均自由程最大，因此气体的稀薄性最强，相应的Kn也最高。由于该中心线交替穿过固体和流体区域，所有工质对应的速度曲线都呈现出波动形式；对于不同气体种类，沿流程的速度波动幅值：氦气>甲烷>氮气>氩气。随着气体压力从入口到出口的下降，气体密度沿着流动方向逐渐减小，速度则逐渐增大。对于不同的气体工质，在相同边界条件下的体积流量相对大小为：Q(氦气)>Q(甲烷)>Q(氮气)>Q(氩气)。然而，由于气体密度的差异，它们对应质量流量的相对大小则相反。在图3（a）的条件下，氦气、甲烷、氮气和氩气在单位长度入口下的质量流量分别为5.53、11.1、14.0和16.5 kg/(m·s)。图3（b）为以氮气为工质并将图3（a）中的固体微元尺寸分别设定为20、100和400 nm时，多孔结构中心线（y=0）上的速度分布。可以看出，不同单元尺度下的速度分布是相似的，且在微元的尾流区域未出现回流现象，这是因为扩散作用相比对流作用更占主导地位。图4分别给出了与上述相同边界条件下微元尺寸为20 nm时的氩气、氮气、甲烷和氦气在单元阵列中速度大小及流线的分布；可以看出，在相同条件下氦气的最大流速远高于氩气和氮气，这是因为氦气具有更大的平均分子自由程，从而导致其Knudsen数比其他分子高得多，同时也证明了气体种类对多孔介质中渗流特性的重要影响。

图3

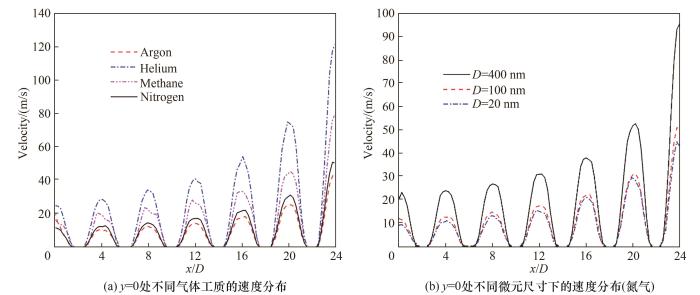
图3 多孔结构中心线（y=0）上的速度分布

Fig.3 Distributions of velocity magnititudes at y=0

图4

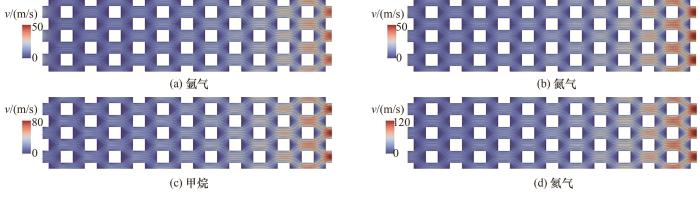
图4 D = 20 nm时氩气、氮气、甲烷和氦气的流速和流线分布

Fig.4 Velocity profiles and streamlines for argon, nitrogen, methane, and helium flows at D = 20 nm

实际上，上述流动规律均可通过稀薄气体表观渗透率模型来进行定量描述。根据Darcy定律，在速度场已知的情况下，多孔介质中可压缩流体的表观渗透率（Ka）可以用式(27)计算：

$K_{a} = \frac{2 μ L p_{o u t} {\bar{u}}_{x, o u t}}{p_{i n}^{2} - p_{o u t}^{2}}$ （27）

式中， ${\bar{u}}_{x, o u t}$ 为多孔介质出口处的气体宏观平均速度。本文对不同孔隙形式（方形、圆形、矩形、立方体）、孔隙率（0.17~0.90）、气体成分（氦气、甲烷、氮气、氩气）以及不同进出口压力下50组不同工况的气体流动状态进行DSMC模拟，并利用式（27）进行表观渗透率计算。通过图5可以发现，如果以式（24）所表示的Knp 为横轴，以相应的Ka/K∞为纵轴，在整个Knp =0.01~10范围内，所有数据点均可近似分布于同一条曲线上。该曲线恰好与本文所提出的理论渗透率模型一致。模拟结果与理论模型的平均相对误差小于10%。

图5

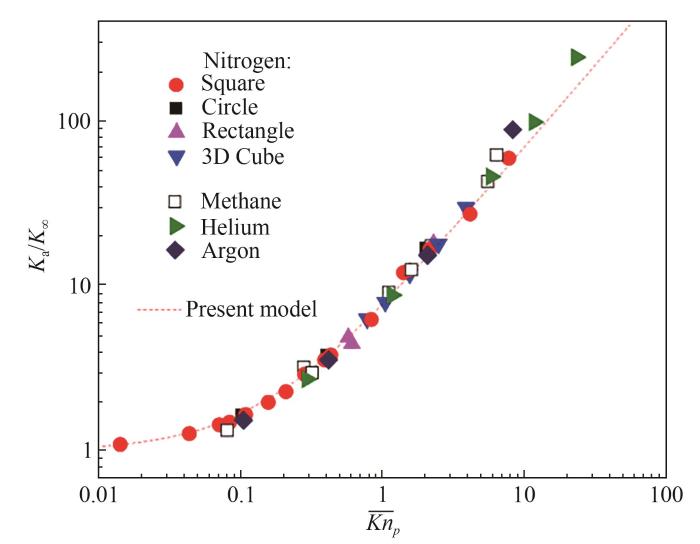
图5 不同Knp 下的表观渗透率与固有渗透率比值

Fig.5 Variation of Ka/K∞ with different Knp

3 结论

多孔结构中稀薄气体流动的表观渗透率是航空航天、能源化工等领域相关应用中的重要参数。本文从多孔结构孔隙的几何拓扑特性出发，将固有渗透率、孔隙率、孔隙弯曲度和孔隙收缩-扩张因子作为基本参数定义了一种新的多孔结构有效孔隙尺寸。将该有效孔隙尺寸与现有的稀薄气体管道流动模型相结合，理论推导出了一种具有通用性的稀薄气体渗透率模型。通过该模型，可以在孔隙三维几何结构和气体的状态参数已知的情况下对多孔结构中稀薄气体的表观渗透率进行预测计算。

为了验证本文所提渗透率模型的准确性，在开源平台OpenFOAM上开展了直接Monte Carlo（DSMC）模拟。对不同孔隙微元形式（方形、圆形、矩形、立方体）、孔隙率（0.17~0.90）、气体成分（氦气、甲烷、氮气、氩气）以及不同进出口压力下共50组不同工况的气体流动状态进行DSMC模拟，并基于模拟结果计算出气体的表观渗透率。气体成分对流动状态的影响显著，在相同的压力边界条件下不同气体的体积流量的相对大小为：氦气>甲烷>氮气>氩气。而由于气体密度的差异，它们质量流量的大小顺序则相反。在整个Knp =0.01~10范围内，不同气体、不同孔隙结构以及不同压力条件下的模拟结果与渗透率模型预测结果间的平均相对误差小于10%。

因此，本文所提出的解析型模型可以充分描述多孔结构中气体流动的Klinkenberg效应，且不依赖于仿真或实验数据作为模型输入条件，为分析和评估微纳尺度或低气压状态下有序性多孔结构的气体渗透率特性提供了一种新的解决思路。

符号说明

B	水力传导系数
C	收缩-扩张因子
D	模型中微单元的特征尺寸，m
k	微元渗透率，m2
L	多孔区域长度，m
R	半径，m
Rc	有效孔隙半径，m
u	流体速度矢量，m/s
V	多孔介质总体积，m3
ρ	气体密度，kg/m3
τ	弯曲度
$ω$	温度系数
下角标
in	入口
out	出口
s	流线

关键字：优秀论文

上一篇：光热驱动多孔氧化铈热化学循环解水制氢非热质平衡模型
下一篇：受限空间内浮升气泡与液体间传质行为实验研究

栏目分类

热门排行

推荐信息

期刊知识