基于热扩散核密度确定密度峰值法的历史工况识别

引 言

近年来，随着物联网、大数据和人工智能等技术的兴起，数据驱动的方法在工业智能化的进程中扮演着重要角色。在实际生产过程中，原料性质、生产方案或操作条件等因素的变动将导致生产过程的多模态化[1]，如发酵过程[2]、冶金过程和锅炉燃烧过程等，对其过程进行数字化时往往存在着非线性、多模态和变量间的强相关性等问题[3-4]。因此，深入研究多模态过程的特点对实际生产有着重要作用。通过获取历史工况特征，不仅可以为当前装置选择合适的工况模型及参数进行优化，也能为生产决策提供重要的数据参考，如污水处理装置的智能优化、管道泄漏的自动化检测和生产运行状况的有效评估[5-6]等。

在对多模态过程的研究中，由于不同工况间存在着较大的差异，研究者通常假设每种工况下的过程数据近似服从一种高斯分布，运用主成分分析（PCA）、偏最小二乘（PLS）、独立成分分析（ICA）和支持向量数据描述（SVDD）模型等方法提取工况数据的特征，然后建立模型应用于过程故障检测、过程控制和过程优化等[7-10]。由于每种工况下的数据具有相似性，有学者将数据聚类的方法用于多模态过程的特征提取[11]。常用的聚类方法包括模糊C均值法[12]、K-均值法[13]、高斯混合模型（GMM）[14-15]和隐马尔可夫模型（HMM）[16]等，这些方法在获取数据特征时具有一定的有效性，但仍存在一些无法避免的缺陷。如K-均值法需要事先确定聚类数量，对数据中的噪声点敏感；模糊C均值法存在聚类数量和参数选取的问题；HMM模型需要事先知道各种模态的概率且固定不变；GMM模型在使用期望最大法求解时，存在计算量较大、对模型参数的初值敏感和容易陷入局部极值等问题，这些缺点都将导致无法准确地识别工况[17-18]。有学者对GMM模型进行深入研究，提出了给定模型参数初值[19]和基于信息准则确定聚类数量[20]的方法，其中F-J的方法较为著名[21-22]，它通过在迭代计算中不断剔除冗余的高斯分量得出聚类结果，但是该方法需要一个较大的聚类数量导致计算量大且收敛困难，其结果的准确性也不能保证。

快速搜索发现密度峰[23]（CFSFDP）是基于局部密度的一种聚类技术，它根据聚类中心点密度较大且与其他中心点距离较远的特点，引入高斯核密度估计函数（KDE）计算数据点的密度，再通过欧氏距离计算数据点间的距离，从而完成数据聚类。但是该方法的聚类效果取决于截距参数，为避免这一点，有学者对其进行改进并提出了无须事先确定截距参数的热扩散核密度确定密度峰的技术[24]（CFSFDP-HD）。本文提出将CFSFDP-HD技术与GMM模型结合的方法，首先通过CFSFDP-HD方法对多模态过程数据进行聚类，然后将聚类结果作为GMM模型的初值，从而对多模态过程的工况进行较准确的估计。

1 工况识别方法

1.1 高斯混合模型

过程数据 X n×d 是d维的n个样本数据，且X={x1,x2,⋯,xn}$X=\left(x_1,x_2,\cdots ,x_n\right)$，其概率密度函数可表示为：

p(x|θ)=∑i=1kτig(x|θi)$p\left(x|\theta \right)=\sum _{i=1}^k{\tau }_{i}g\left(x|{\theta }_i\right)$(1)

其中，k为高斯模型的数量，τi 和θi={μi,Σi}${\theta }_i=\left({\mu }_i,{\Sigma }_i\right)$分别为第i个高斯模型的权重和参数（平均值和协方差）。

第i个高斯模型对应的高斯密度函数为：

g(x|θi)=1(2π)d/2|Σi|1/2exp[−12(x−μi)TΣ−1i(x−μi)]                         (i=1,2,⋯,k)$\begin{array}{c}g\left(x|{\theta }_i\right)=\frac{1}{{\left(2\pi \right)}^{d/2}{\left({\Sigma }_i\right)}^{1/2}}exp\left(-\frac{1}{2}{\left(x-{\mu }_i\right)}^{{\rm T}}{\Sigma }_i^{-1}\left(x-{\mu }_i\right)\right)\\ \left(i=\mathrm{1,2},\cdots ,k\right)\end{array}$(2)

模型的参数θi 常用EM法[25]求解，通过不断地更新后验概率和模型参数，直到模型参数几乎不变。针对数据X={x1,x2,⋯,xn}$X=\left(x_1,x_2,\cdots ,x_n\right)$和模型初始参数θ(0)={{τ(0)1,θ(0)1},{τ(0)2,θ(0)2},…,{τ(0)k,θ(0)k}}${\theta }^{\left(0\right)}=\left(\left({\tau }_1^{\left(0\right)},{\theta }_1^{\left(0\right)}\right),\left({\tau }_2^{\left(0\right)},{\theta }_2^{\left(0\right)}\right),\dots ,\left({\tau }_k^{\left(0\right)},{\theta }_k^{\left(0\right)}\right)\right)$，其迭代计算步骤如下。

E步骤：

P(s)(Ck|xj)=τ(s)kg(xj|μ(s)k,Σ(s)k)∑i=1kτ(s)ig(xj|μ(s)i,Σ(s)i)         (j=1,2,⋯,n)$P^{\left(s\right)}\left(C_k|x_j\right)=\frac{{\tau }_k^{\left(s\right)}g\left(x_j|{\mu }_k^{\left(s\right)},{\Sigma }_k^{\left(s\right)}\right)}{\sum _{i=1}^k{\tau }_i^{\left(s\right)}g\left(x_j|{\mu }_i^{\left(s\right)},{\Sigma }_i^{\left(s\right)}\right)}\left(j=\mathrm{1,2},\cdots ,n\right)$(3)

P(s)(Ck|xj)$P^{\left(s\right)}\left(C_k|x_j\right)$表示第j个样本属于第k个高斯模型的后验概率，s表示第s次迭代。

M步骤：

μ(s+1)k=∑j=1nP(s)(Ck|xj)xj∑j=1nP(s)(Ck|xj)${\mu }_k^{\left(s+1\right)}=\frac{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)x_j}{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)}$(4)Σ(s+1)k=∑j=1nP(s)(Ck|xj)(xj−μ(s+1)k)(xj−μ(s+1)k)T∑j=1nP(s)(Ck|xj)${\Sigma }_k^{\left(s+1\right)}=\frac{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)\left(x_j-{\mu }_k^{\left(s+1\right)}\right){\left(x_j-{\mu }_k^{\left(s+1\right)}\right)}^{{\rm T}}}{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)}$(5)τ(s+1)k=∑j=1nP(s)(Ck|xj)n${\tau }_k^{\left(s+1\right)}=\frac{\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)}{n}$(6)

其中，μ(s+1)k、Σ(s+1)k、τ(s+1)k${\mu }_k^{\left(s+1\right)}、{\Sigma }_k^{\left(s+1\right)}、{\tau }_k^{\left(s+1\right)}$分别为第k个高斯模型在第（s+1）次迭代的平均值、协方差矩阵和先验概率。

基于最短信息长度准则的F-J方法只需对式（6）进行如下修改，即可得到较为理想的聚类结果。

τ(s+1)k=max{0,(∑j=1nP(s)(Ck|xj))−v2}∑i=1kmax{0,(∑j=1nP(s)(Ck|xj))−v2}${\tau }_k^{\left(s+1\right)}=\frac{max\left(0,\left(\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)\right)-\frac{v}{2}\right)}{\sum _{i=1}^{k}max\left(0,\left(\sum _{j=1}^n{P}^{\left(s\right)}\left(C_k|x_j\right)\right)-\frac{v}{2}\right)}$(7)

其中，v=12d2+32d$v=\frac{1}{2}{d}^2+\frac{3}{2}d$，d为变量的个数，通过迭代将任意两个相同的高斯模型进行合并，最终获得多个工况模型及其参数。

1.2 热扩散核密度确定密度峰技术

基于热扩散的高斯核函数为：

P(di,dj,t)=1n∑j=1n12πt√e−(di−dj)22t$P\left(d_i,d_j,t\right)=\frac{1}{n}\sum _{j=1}^n\frac{1}{\sqrt[]{2\pi t}}{e}^{-\frac{{\left(d_i-d_j\right)}^2}{2t}}$ （j =1,2,…,n）(8)

P(di,dj,t)$P\left(d_i,d_j,t\right)$为样本点i到j的转移概率，t为核函数的带宽，di - dj 为样本j到i的距离。

估算任意样本点i的概率密度函数为：

ρi=f⌢(d;t)≈∑k=0n−1αke−k2π2t/2cos(kπd)${\rho }_i=\stackrel{⌢}{f}\left(d;t\right)\approx \sum _{k=0}^{n-1}{\alpha }_k{e}^{-k^2{\pi }^{2}t/2}cos\left(k\pi d\right)$(9)

式（9）为KDE的完全自适应形式，考虑了最佳带宽选择和边界校正。其中n为一个较大的整数，本文取n为样本数量，αk 为：

αk=⎧⎩⎨⎪⎪⎪⎪1,k=01n∑i=1ncos(kπdi),k=1,2,⋯,n−1${\alpha }_k=\left(\begin{array}{c}\begin{array}{cc}1,& k=0\end{array}\\ \begin{array}{cc}\frac{1}{n}\sum _{i=1}^{n}cos\left(k\pi d_i\right),& k=\mathrm{1,2},\cdots ,n-1\end{array}\end{array}\right)$(10)

最佳带宽的选择使用了改进的Sheather–Jones(ISJ)方法[26]，其计算步骤如下：

t=ξγ[l](t)$t=\xi {\gamma }^{\left(l\right)}\left(t\right)$(11)ξ=62√−37$\xi =\frac{6\sqrt[]{2}-3}{7}$(12)γ[l](t)=γ1(γ2(⋯γl(t)⋯))${\gamma }^{\left(l\right)}\left(t\right)={\gamma }_1\left({\gamma }_2\left(\cdots {\gamma }_l\left(t\right)\cdots \right)\right)$(13)γ[l](t)=1+0.5(l+0.5)31×3×⋯×(2l−1)nπ/2√∥∥f(l+1)∥∥2${\gamma }^{\left(l\right)}\left(t\right)=\frac{1+0.5^{\left(l+0.5\right)}}{3}\frac{1\times 3\times \cdots \times \left(2l-1\right)}{n\sqrt[]{\pi /2}{\left(f^{\left(l+1\right)}\right)}^2}$(14)∥∥f(l+1)∥∥2=∑k=1l−1(kπ)(2l+2)α2kexp(−(kπ)2t)${\left(f^{\left(l+1\right)}\right)}^2={\sum _{k=1}^{l-1}\left(k\pi \right)}^{\left(2l+2\right)}{\alpha }_k^{2}exp\left(-{\left(k\pi \right)}^{2}t\right)$(15)

其中，当l ≥ 5时，l的取值对式（11）的计算结果影响很小，故本文中取l = 5。

带宽t的详细求解步骤如下：

（1）设置一个较小的容差ε = 10-9，令yq=ε，q = 0；

（2）计算yq+1=ξγ[l](yq)$y_{q+1}=\xi {\gamma }^{\left(l\right)}\left(y_q\right)$；

（3）如果∣∣yq+1−yq∣∣<ε$\left(y_{q+1}-y_q\right)<\epsilon$，t = yq+1停止，否则yq = yq+1，q = q +1，返回步骤（2）。另外，令t = sqrt(t)/3.3，可对边界点进行修正。

计算每一样本点i到最近的高密度点j的距离：

δ={min(dij), if ∃ j, ρj>ρimax(dij), otherwise$\delta =\left(\begin{array}{c}min\left(d_{ij}\right),if\exists j,{\rho }_j>{\rho }_i\\ max\left(d_{ij}\right),otherwise\end{array}\right)$(16)

1.3 提出方法的计算步骤

本文提出的方法对近似服从高斯分布的未知多模态稳态工况进行识别时，首先利用CFSFDP-HD技术对多模态过程数据进行聚类，确定聚类中心点及其个数（即工况个数），然后将每一类数据的平均值和协方差作为GMM模型的初值，迭代求出不同工况的特征参数。其计算过程如下：

（1）将数据标准化处理，求取参数αk；

（2）由参数αk 和式（11）~式（15）得出最佳带宽t；

（3）由式（9）和式（16）的结果画出决策图，并由此完成聚类；

（4）将每一类的特征参数作为GMM模型初值，求出最终工况参数。

通过以上步骤即可完成对历史工况的准确识别，下面通过第2节中的两个例子对该方法进行验证。

图1

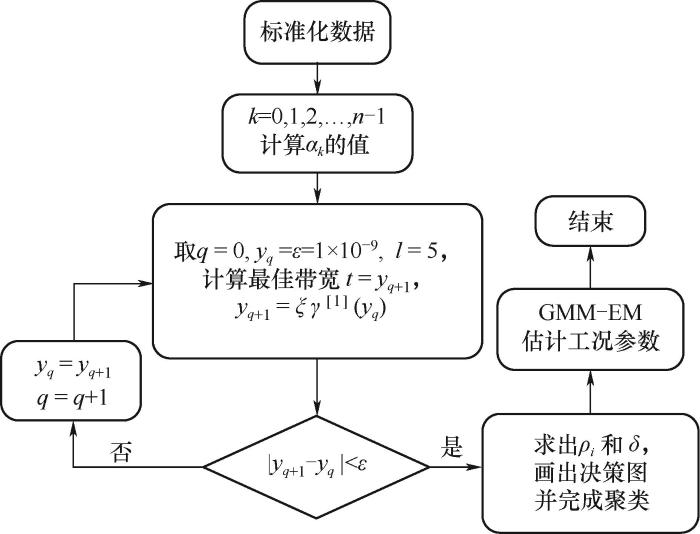
图1   基于热扩散核密度的工况识别方法流程图

Fig.1   Flow chart of recognizing operating modes based on kernel density estimation of heat diffusion

2 方法验证与结果分析

2.1 仿真数据

根据文献[27]中的多模态仿真模型生成过程数据，然后分别用本文提出的方法、K-均值法和GMM（F-J）的方法进行工况识别，数据生成模型如式（17）所示：

⎧⎩⎨⎪⎪x1=0.5768s1+0.3766s2+e1x2=0.7382s21+0.0566s2+e2x3=0.8291s1+0.4009s22+e3$\left(\begin{array}{c}{x}_1=0.5768s_1+0.3766s_2+e_1\\ x_2=0.7382s_1^2+0.0566s_2+e_2\\ x_3=0.8291s_1+0.4009s_2^2+e_3\end{array}\right)$(17)x˜i=xi,j−xi,minxi,max−xi,min${\tilde{x}}_i=\frac{x_{i,j}-x_{i,min}}{x_{i,max}-x_{i,min}}$(18)

式（18）为数据标准化的方法，xi,j 表示第i个变量的第j个数据，x˜i${\tilde{x}}_i$表示标准化处理后的第i个变量的向量数据，xi,min表示第i个变量的最小值，xi,max表示第i个变量的最大值。

其中,e1~e3是服从[0，0.01]的高斯白噪声分布，通过调整s1和s2的参数，生成含3个变量（x1、x2和x3）的多模态过程数据。其中模态1是变量s1和s2分别服从高斯分布为[20，0.8]、[1，1.3]得到的300个数据；模态2是变量s1和s2分别服从高斯分布[5，0.6]、[20，0.7]得到的300个数据；模态3是变量s1和s2分别服从高斯分布[16，1.5]、[20，0.7]得到的300个数据；模态4是和模态2在相同参数（工况）下产生的300个数据，用于检验三种方法能否准确地获取实际的工况状态。

将生成数据用式（18）进行标准化处理，其分布情况如图2所示，可以看出数据有四个阶段，其中300~600和900~1200阶段的状态相同，然后分别对三种方法进行验证。使用本文方法画出关于密度和距离的决策图，见图3，图中有三个中心点，表明本文方法根据过程数据识别出三种工况，每个中心点表示一种工况的数据中心。然后根据数据点到中心点的距离将其分类，将每一类的结果作为GMM模型的初值，从而得出不同工况的特征参数。使用K-均值法进行工况识别时，由于聚类数量是未知的，所以将聚类数量分别设置为3、4和5，其中K = 5时的结果与实际相差较大，其结果未在表1中列出。使用GMM（F-J）方法时，需要设置初始聚类数量（K）大于实际工况数量，本文分别设为4、5和6，GMM模型的初值设置为将过程数据平均分成K份，每份数据的特征参数[19]，先验概率设为1/K，其中K = 6时的结果与K = 5时的结果几乎相同，其结果未在表1中列出。三种方法的工况识别结果见表1。可以看出本文方法获取的多模态过程的工况个数及其特征参数（变量的平均值和工况的先验概率）与实际值一致。当K-均值法的聚类数量与实际工况数量一致时（K=3），得到的工况特征参数与实际值的相对偏差较小，当聚类数量大于实际工况数量时（K=4），得到的工况特征参数与实际值的相对偏差较大，由此看出该方法的工况识别效果取决于聚类数量的准确选择。GMM（F-J）方法给定不同的初始聚类数量（K=4、5）时均将工况识别为4种，未能准确识别出实际工况的个数，但得到的工况特征参数与实际值的偏差在0.01~-20.39，其结果仍具有一定的参考价值。

图2

图2   仿真多模态过程数据标准化

Fig.2   Normalization of multi-modal process simulation data

图3

图3   仿真多模态过程数据的聚类中心决策图

Fig.3   Clustering center decision diagram of process data for simulating multiple operating modes

表1   仿真多模态过程的工况识别结果

Table 1  Recognition results of simulation multiple operating modes

2.2 TE过程

Tennessee Eastman（TE）工业过程是由美国Eastman化学品公司开发的复杂工业过程的仿真平台，它包括六种工作模态，每种模态具有不同的产品比例（G/H），该流程包含12个操作变量、22个连续过程测量变量和19个组成测量变量[28-30]。本文选取TE过程中模态1~模态4作为多模态过程，选取41个测量变量作为工况识别的变量，其中每种模态取300个数据为1组，第5组和第3组为相同模态下的数据，具体模态选取情况见表2。

表2   TE过程的模态选取情况

Table 2  Mode selection of the TE process

将过程数据用式（18）进行标准化处理，选取反应器温度、A和C的混合进料量、产品分离器压力和回收流量4个变量画出分布图，见图4，可以看出5个阶段中600~900和1200~1500的状态相同，然后分别用三种方法进行验证。本文方法得到的决策图见图5，图中有4个中心点，表明本文方法识别出4种工况，然后使用GMM法获取每种工况的特征参数。将K-均值法的聚类数量（K）分别设为4、5和6，其中K = 5和6的结果与实际相差较大，其结果未在表4中列出。将GMM（F-J）方法的初始聚类数量设为4、5和6时，该方法均无法获取工况参数。三种方法工况识别结果的典型数据见表3、表4。

图4

图4   4个TE过程变量的标准化

Fig.4   Normalization of 4 TE process variables

图5

图5   TE多模态过程数据的聚类中心决策图

Fig.5   Clustering center decision diagram of TE multi-modal process

表3   TE多模态过程的工况个数及先验概率的识别结果

Table 3  Recognition results of the number and probability of the TE multi-modal process

表4   TE多模态过程变量的识别结果

Table 4  Recognition results of TE multi-modal process variables

从表3可以看出本文方法得到的历史工况的个数和先验概率与实际值一致；K-均值法的结果则取决于设定的聚类数量K，当K与实际一致（K = 4）时也可以较准确获取历史工况的个数及先验概率，但是当K = 5和K = 6时，其结果与实际相差较大。GMM（F-J）法则无法获取到工况的参数。

三种方法过程变量的识别结果见表4，可以看出本文提出的方法识别结果的平均相对偏差在 -0.0043~-1.3681，最大相对偏差为-4.748，最小相对偏差为-0.0014；K-均值法识别结果的平均相对偏差在-0.0043~-1.4371，最大相对偏差为-4.9847，最小相对偏差为-0.0014。结合表3、表4可以看出GMM（F-J）法不适合本案例的工况识别，本文方法和给定准确聚类数量的K-均值法都可以较准确地识别出工况特征，但K-均值法的准确性依赖于聚类数量的选择，而本文方法则没有这种约束。

3 结 论

针对目前工况识别方法的不足，提出将人工智能领域的CFSFDP-HD技术与GMM模型结合用于对多模态过程的历史工况进行识别的方法，避免了K-均值法需要预先提供准确聚类数量的缺点，并利用案例对本文所提方法进行了验证，结果表明：GMM（F-J）法不能保证准确地识别工况，K-均值法只有在给定正确工况数量的前提下才能获得较好的结果，而本文方法则可方便、有效地对历史多工况进行准确识别，具有更强的实用性。

符 号 说 明